A uniform wire of resistance 4Ω is bent into circle of radius r. As specimen of the same wire is connected along the dimeter of the circle. What is the equivalent resistance across the ends of this wire?
4(4+π)Ω
3(3+π)Ω
2(2+π)Ω
1(1+π)Ω
The correct Answer is:A
To solve the problem step by step, we will analyze the given information and apply the relevant formulas.
Step 1: Understand the configuration
We have a uniform wire with a total resistance of R=4Ω. This wire is bent into a circle of radius r. We also have a specimen of the same wire connected along the diameter of the circle.
Step 2: Determine the length of the wire
The total length of the wire when bent into a circle is given by the circumference of the circle:
L=2πr
Since the resistance of the entire wire is 4Ω, we can find the resistance per unit length of the wire:
Resistance per unit length=RL=4Ω2πr=2πrΩ/m
Step 3: Calculate the resistance of the semicircle
When the wire is bent into a circle, the wire can be considered as two semicircles when we connect the wire along the diameter. The resistance of each semicircle is half of the total resistance of the circle:
Rsemicircle=R2=4Ω2=2Ω
Step 4: Calculate the resistance of the diameter
The length of the wire along the diameter is equal to the diameter of the circle:
Length along diameter=2r
Now, we can find the resistance of the wire along the diameter:
Rdiameter=Resistance per unit length×Length along diameter=(2πr)×(2r)=4πΩ
Step 5: Combine resistances
Now we have three resistances to consider:
1. Resistance of the left semicircle: R1=2Ω
2. Resistance of the right semicircle: R2=2Ω
3. Resistance of the wire along the diameter: R3=4πΩ
These resistances are in parallel. The formula for the equivalent resistance RAB for resistors in parallel is given by:
1RAB=1R1+1R2+1R3
Substituting the values:
1RAB=12+12+π4
1RAB=1+π4
RAB=11+π4=44+πΩ
Final Answer
The equivalent resistance across the ends of the wire is:
RAB=44+πΩ
We have a uniform wire with a total resistance of R=4Ω. This wire is bent into a circle of radius r. We also have a specimen of the same wire connected along the diameter of the circle.
The total length of the wire when bent into a circle is given by the circumference of the circle:
L=2πr
Since the resistance of the entire wire is 4Ω, we can find the resistance per unit length of the wire:
Resistance per unit length=RL=4Ω2πr=2πrΩ/m
When the wire is bent into a circle, the wire can be considered as two semicircles when we connect the wire along the diameter. The resistance of each semicircle is half of the total resistance of the circle:
Rsemicircle=R2=4Ω2=2Ω
The length of the wire along the diameter is equal to the diameter of the circle:
Length along diameter=2r
Now, we can find the resistance of the wire along the diameter:
Rdiameter=Resistance per unit length×Length along diameter=(2πr)×(2r)=4πΩ
Now we have three resistances to consider:
1. Resistance of the left semicircle: R1=2Ω
2. Resistance of the right semicircle: R2=2Ω
3. Resistance of the wire along the diameter: R3=4πΩ
1RAB=1R1+1R2+1R3
Substituting the values:
1RAB=12+12+π4
1RAB=1+π4
RAB=11+π4=44+πΩ
The equivalent resistance across the ends of the wire is:
RAB=44+πΩ
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - DC PANDEYCHAPTER - CURRENT ELECTRICITYEXERCISE - OBJECTIVE_TYPE
1 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEYCHAPTER - CURRENT ELECTRICITYEXERCISE - Level 1 Subjective
53 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEYCHAPTER - CURRENT ELECTRICITYEXERCISE - Level 1 Assertion And Reason
11 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEYCHAPTER - COMMUNICATION SYSTEMEXERCISE - Subjective
11 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Medical entrances gallery
25 Videos
Similar Questions
Knowledge Check
A wire of resistance 0.5ωm−1 is bent into a circle of radius 1m. The same wire is connected across a diameter AB as shown in fig. The equivalent resistance is
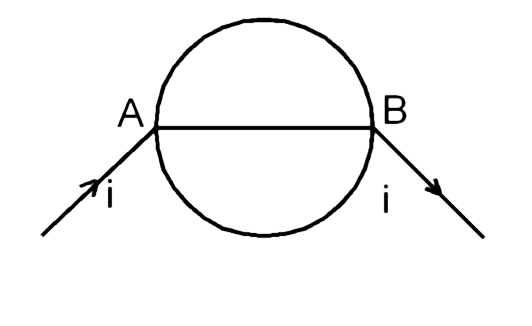 AπohmBπ(π+2)ohmCπ(π+4)ohmD(π+1)ohm
AπohmBπ(π+2)ohmCπ(π+4)ohmD(π+1)ohmA uniform wire of resistance 18Ω is bent in the form of a circle. The effective resistance across the points a and b is
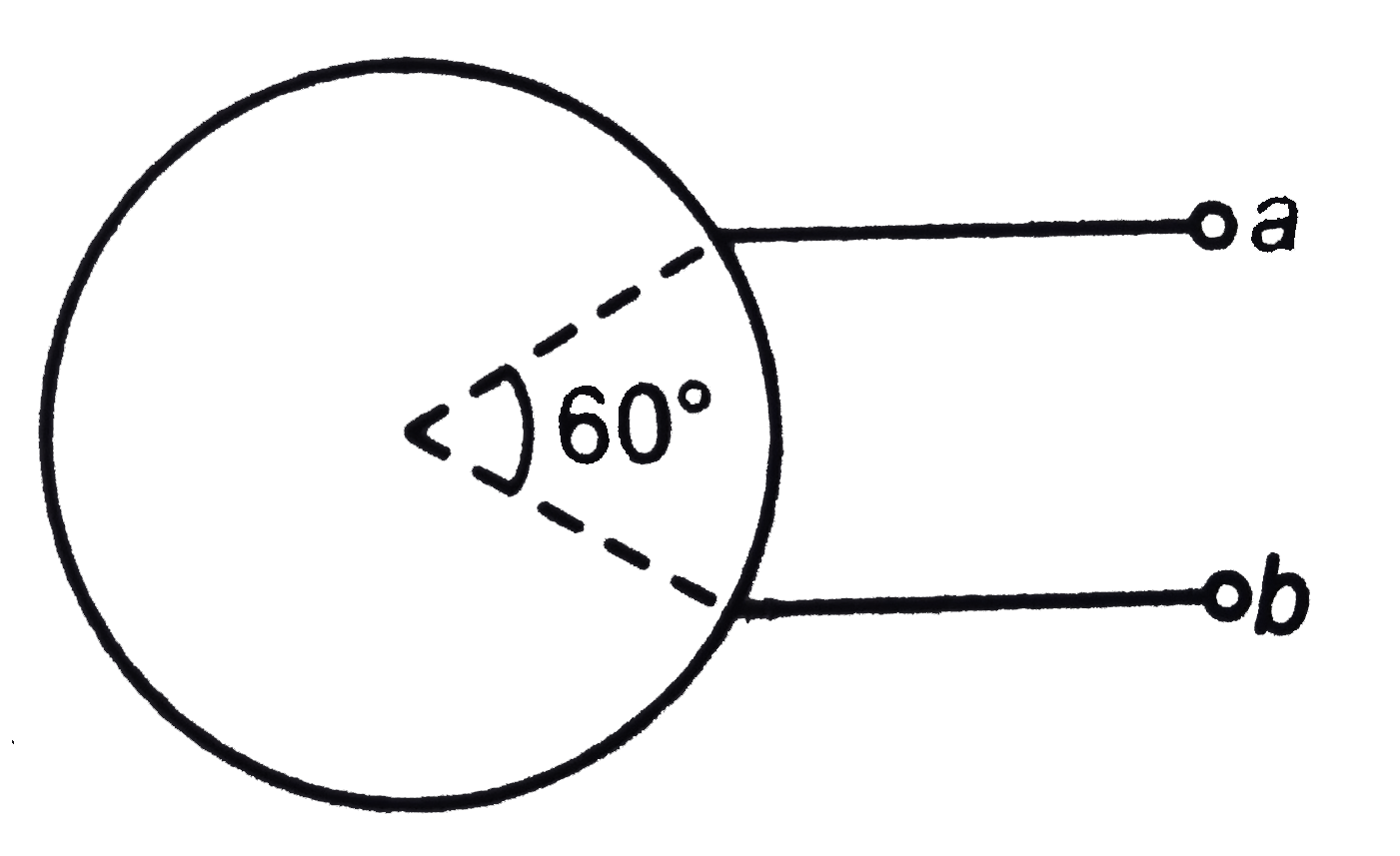 A3ΩB2ΩC2.5ΩD6Ω
A3ΩB2ΩC2.5ΩD6ΩA uniform wire os resistance 12Ω is bent to form a circle. Effective resistance across two diametrically opposite points is
A12ΩB24ΩC3ΩD6Ω
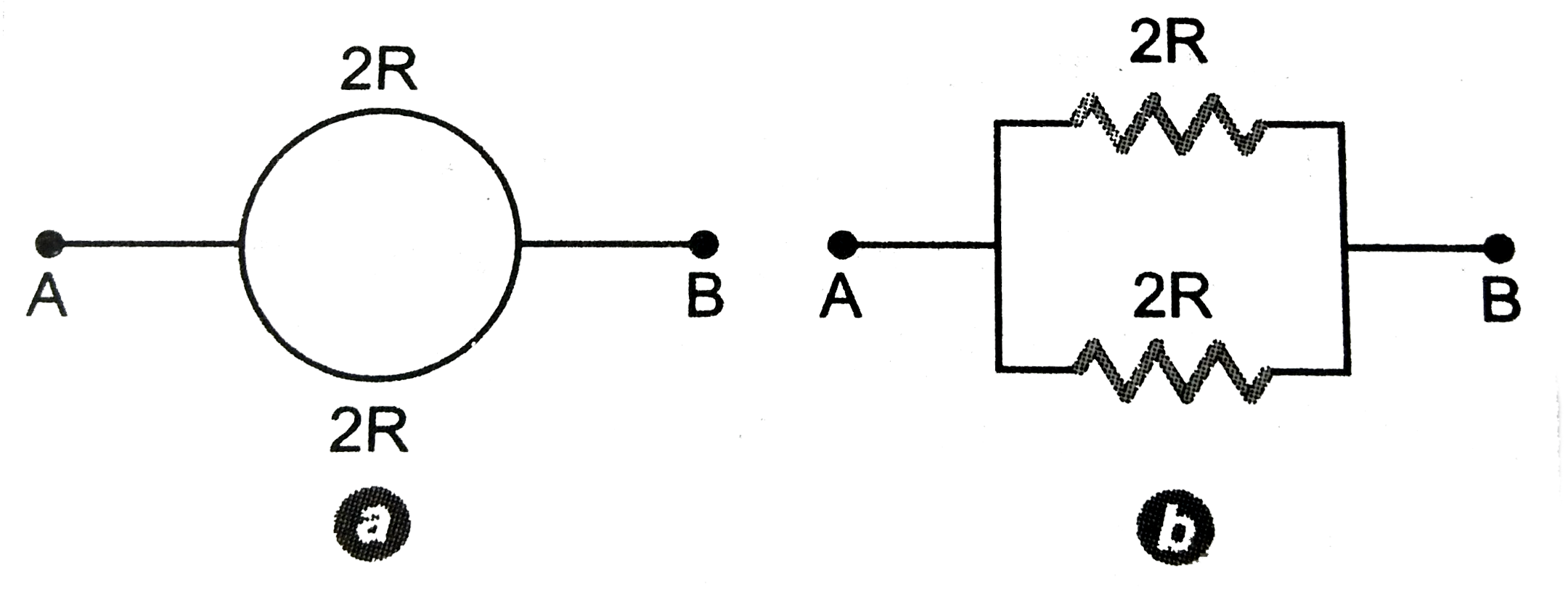
A wire of resistance 4 R is bent in the form of a circle [Fig 4.4]. What is the effective resistance between the ends of the diameter ?

View SolutionA wire of resistance 8R is bent in the form of a circle. What is the effective resistance between the ends of a diameter AB?
View SolutionWhat is the resistance of a connecting wire ?
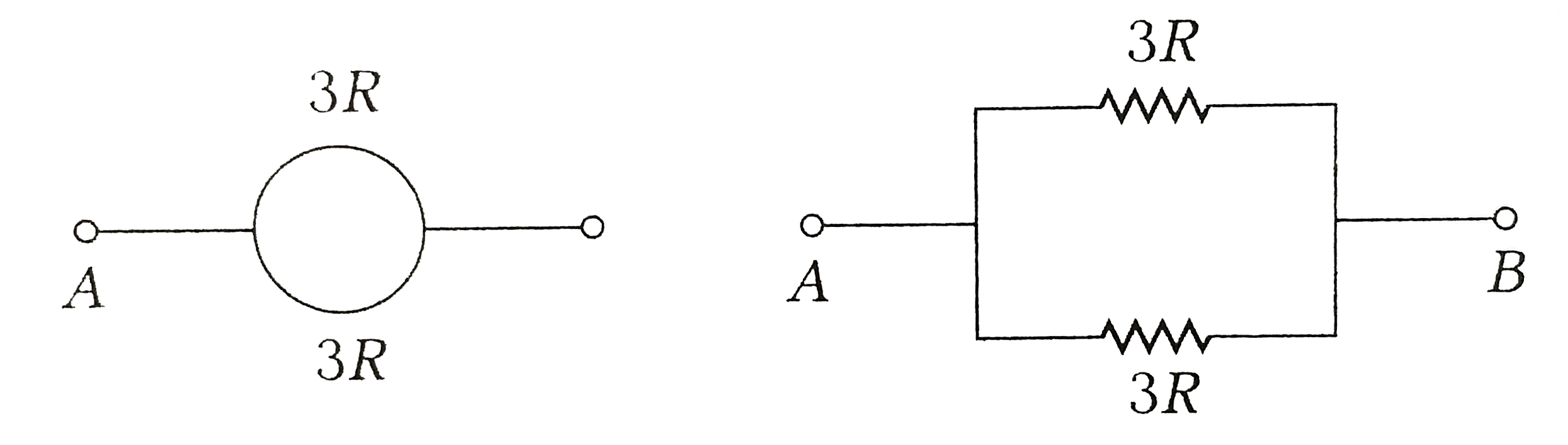
View SolutionA wire of resistance 5Ω is bent in the form of a closed circle. Find the resistance across the diameter of the circle.
View SolutionA uniform wire of resistance 36Ω is bent in the form of a circle. The effective resistance across the points A and B is

View Solution