Question

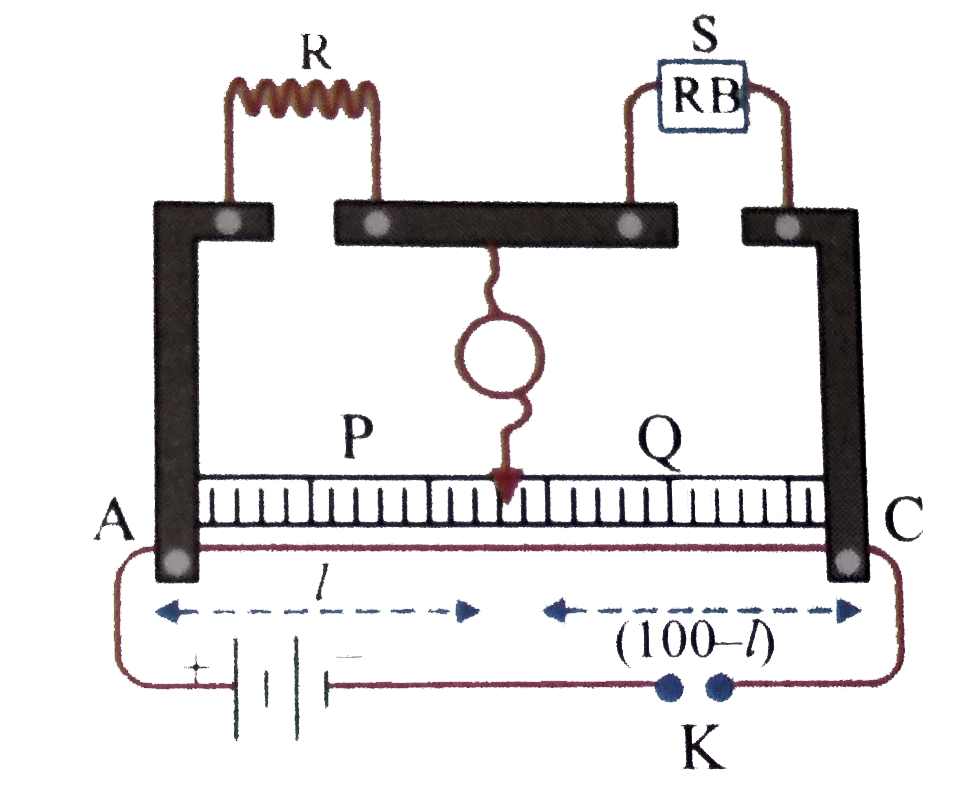
If resistance $R_1$ in resistance box is $300\Omega$ then the balanced length is found to be $75.0cm$ from end $A$. The diameter of unknown wire is 1 mm and length of the unknown wire is $31.4cm$. Find the specific resistance of the unknown wire

Explanation

To find the specific resistance (resistivity) of the unknown wire, we will follow these steps:

Step 1: Understand the given data
- Resistance in the resistance box, \( R_1 = 300 \, \Omega \)
- Balanced length from end A, \( L_A = 75.0 \, \text{cm} \)
- Length of the unknown wire, \( L = 31.4 \, \text{cm} = 0.314 \, \text{m} \)
- Diameter of the unknown wire, \( d = 1 \, \text{mm} = 1 \times 10^{-3} \, \text{m} \)

Step 2: Calculate the length from end B
Since the total length of the meter bridge is 100 cm, the length from end B is:
\( L_B = 100 \, \text{cm} - L_A = 100 \, \text{cm} - 75.0 \, \text{cm} = 25.0 \, \text{cm} \)

Step 3: Use the balance condition to find the unknown resistance \( X \)
According to the meter bridge principle, we have:
\( \frac{R_1}{X} = \frac{L_A}{L_B} \)
Substituting the known values:
\( \frac{300 \, \Omega}{X} = \frac{75.0 \, \text{cm}}{25.0 \, \text{cm}} \)
This simplifies to:
\( \frac{300}{X} = 3 \)
Cross-multiplying gives:
\( X = \frac{300}{3} = 100 \, \Omega \)

Step 4: Calculate the area \( A \) of the wire
The area \( A \) of the wire can be calculated using the formula for the area of a circle:
\( A = \frac{\pi d^2}{4} \)
Substituting the diameter:
\( A = \frac{\pi (1 \times 10^{-3})^2}{4} = \frac{\pi (1 \times 10^{-6})}{4} = \frac{\pi}{4} \times 10^{-6} \, \text{m}^2 \)

Step 5: Calculate the specific resistance \( \rho \)
Using the formula for specific resistance:
\( \rho = \frac{R \cdot A}{L} \)
Substituting the values:
\( \rho = \frac{100 \, \Omega \cdot \left(\frac{\pi}{4} \times 10^{-6} \, \text{m}^2\right)}{0.314 \, \text{m}} \)
Calculating this gives:
\( \rho = \frac{100 \cdot \frac{3.14 \times 10^{-6}}{4}}{0.314} \)
\( \rho = \frac{100 \cdot 0.785 \times 10^{-6}}{0.314} = \frac{78.5 \times 10^{-6}}{0.314} \approx 2.5 \times 10^{-4} \, \Omega \, \text{m} \)

Final Answer
The specific resistance of the unknown wire is approximately:
\( \rho \approx 2.5 \times 10^{-4} \, \Omega \, \text{m} \)