Two conducting rods when connected between two points at constant but different temperatures separately, the rate of heat flow through them is q1andq2.
When they are connected in series, the net rate of heat flow is q1+q2
When they are connected in series, the net rate of heat flow is (q1q2q1+q2)
When they are connected in parallel, the net rate of heat flow is q1+q2
Both (b) and (c)
The correct Answer is:D
q1=TDR1
R1=TDq1
Similarly, R2=TDq2
In series,
qs=TDR1+R2=TD(TDq1)+(TDq2)
=q1q2q1+q2
In parallel, qp=TDR≠t=(TD)(1R≠t)
=TD(1R1+1R2)
=TD(q1TD+q2TD)=q1+q2 .
Topper's Solved these Questions
- CALORIMETRY & HEAT TRANSFERBook:DC PANDEYChapter:CALORIMETRY & HEAT TRANSFERExercise:Level 2 Subjective
Explore 14 Videos
- CALORIMETRY & HEAT TRANSFERBook:DC PANDEYChapter:CALORIMETRY & HEAT TRANSFERExercise:Level 2 Single Correct
Explore 7 Videos
- BASIC MATHEMATICSBook:DC PANDEYChapter:BASIC MATHEMATICSExercise:Exercise
Explore 13 Videos
- CALORIMETRY AND HEAT TRANSFERBook:DC PANDEYChapter:CALORIMETRY AND HEAT TRANSFERExercise:Medical entrance s gallery
Explore 38 Videos
Similar Questions
The three rods described in the previous question are placed individually, with their ends kept at the same temperature difference. The rate of heat flow through C is equal to the rate of combined heat flow through A and B. kc must be equal to
View SolutionTwo conductors AB and CD are connected between two parallel resistors in such a way that no current flows through them. Then a wire is connected between between E and F.
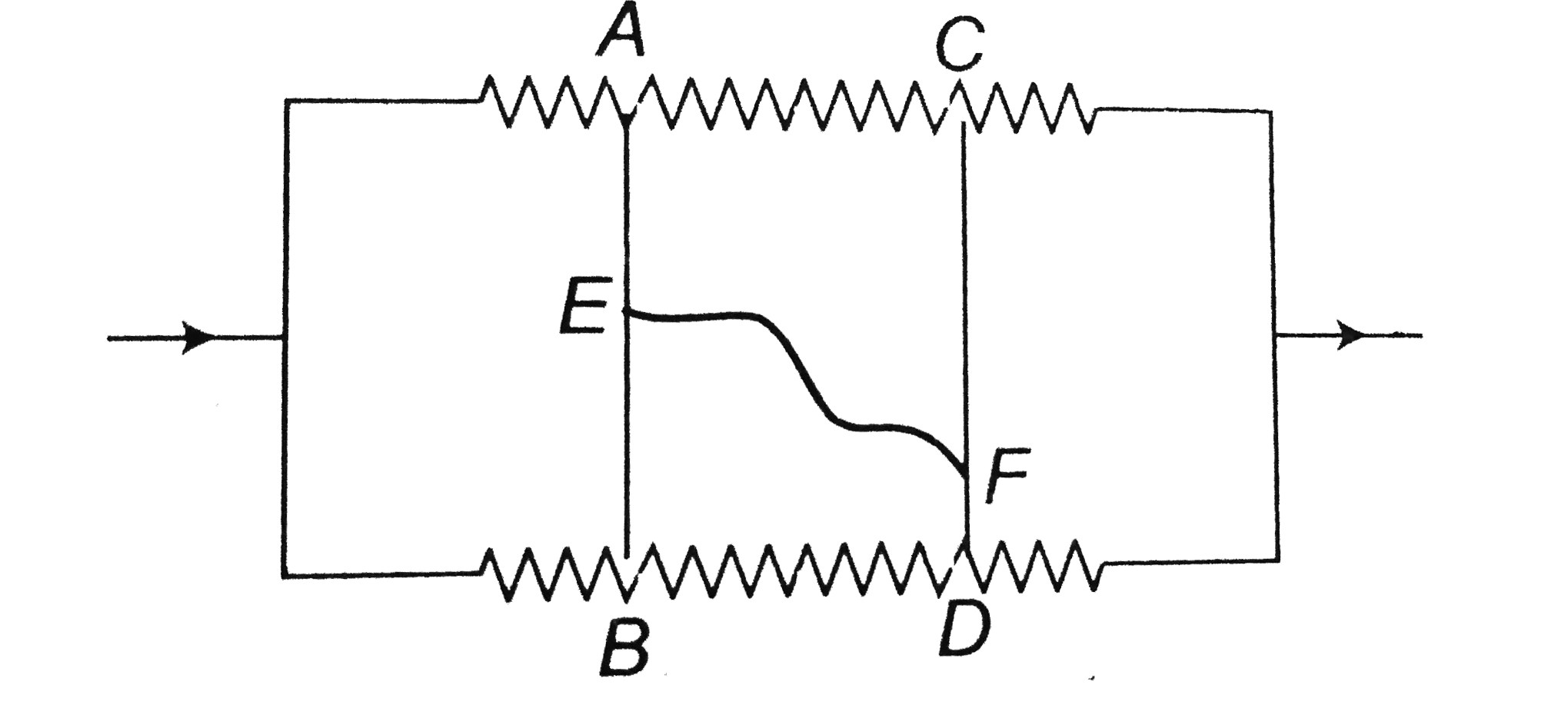
View Solution
Knowledge Check
When two bodies at different temperature are kept in contact. Net heat flow takes place between them till-
AThermal equilibrium has reachedBTemperature of both the bodies become sameCInternal energies of both the bodies become equalDNone of theseTwo cylindrical rods of same meterial have the same temperature difference between their ends. The ratio of rates of flow of heat through them is 1 : 8. The ratio of the radii of the rods are 1 : 2. What is the ratio of their lengths ?
A2:1B4:1C1:8D1:32Two identical rods with different thermal conductivities k1 & k2 and different temperatures are first placed along length and then along area, then the ratio of rates of heat flow in both cases is
A4k1k2(k1+k2)2BnoneC(k1+k2k1−k2)Dk1k2(k1+k2)2
A and B are two points on uniform metal ring whose centre is O The angle AOB=θ A and B are maintaind at two different constant temperatures When θ=180∘ the rate of total heat flow from A to B is 1.2W When θ=90∘ this rate will be .
View SolutionThe heat is flowing through two cylinderical rods of same material. The diameters of the rods are in the ratio 1:2 and their lengths are in the ratio 2:1. If the temperature difference between their ends is the same, the ratio of rates of flow of heat through them will be
View SolutionTwo conducting spheres of radius R and 3R carry charges Q and −2Q. Between these spheres a neutral conducting sphere of radius 2R is connected. The separation between the sphere is considerably large Charge flows through conducting wire due to potential difference.

The final charge on initially neutral conducting sphere is :
View SolutionThe lengths and radii of two rods made of same material are in the ratios 1 : 2 and 2 : 3 respectively. If the temperature difference between the ends for the two rods be the same, then in the steady state, the amount of heat flowing per second through them will be in the ratio
View SolutionTwo conducting spheres of radius R and 3R carry charges Q and −2Q. Between these spheres a neutral conducting sphere of radius 2R is connected. The separation between the sphere is considerably large Charge flows through conducting wire due to potential difference.

The final electric potential of sphere of radius 3R will be :
View Solution