The volume of one mode of an ideal gas with adiabatic exponent γ is varied according to the law V=a/T, where a is constant . Find the amount of heat obtained by the gas in this process, if the temperature is increased by ΔT.
The correct Answer is:A, B, D
V=aT
or
VT=constant
or V(pV)=constant
∴ pV2=constant
In the process pVx=constant, molar heat capacity is
C=Rγ−1+R1−x
Here, x=2
∴ C=Rγ−1+R1−2=(2−γγ−1)R
Now, Q=nCΔT
=(1)(2−γγ−1)RΔT
=(2−γγ−1)RΔT
Topper's Solved these Questions
- LAWS OF THERMODYNAMICSBOOK - DC PANDEYCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Level 2 Passage II
3 Videos
- LAWS OF MOTIONBOOK - DC PANDEYCHAPTER - LAWS OF MOTIONEXERCISE - Medical entrances gallery
39 Videos
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBOOK - DC PANDEYCHAPTER - MAGNETIC EFFECT OF CURRENT AND MAGNETISMEXERCISE - Integer type Questions
10 Videos
Similar Questions
The volume of one mole of an ideal gas with adiabatic exponent γ=1.4 is vaned according to law V=a/T where 'a' is a constant. Find amount of heat absorbed by gas in this process if gas temperature increases by 100 K.
View SolutionAn ideal gas has adiabatic exponenty. It expands according to the law P=αV, where is αconstant. For this process, the Bulk modulus of the gas is
View Solution
Knowledge Check
The volume of one mode of an ideal gas with adiabatic exponent γ is varied according to the law V=a/T, where a is constant . Find the amount of heat obtained by the gas in this process, if the temperature is increased by ΔT.
A(1−γγ+1)R△TBRγ−1△TC(2−γγ−1)R△TDR△Tγ−1The volume of one mole of ideal gas with adiabatic exponent is varied according to law V=1T. Find amount of heat obtained by gas in this process if gas temperature is increased by 100 K.
A100RB200RC300RD400RThe efficiency of an ideal gas with adiabatic exponent 'γ' for the shown cyclic process would be
 A(2ln2−1)γ/(γ−1)B(1−2ln2)γ/(γ−1)C(2ln2+1)γ/(γ−1)D(2ln2−1)γ/(γ+1)
A(2ln2−1)γ/(γ−1)B(1−2ln2)γ/(γ−1)C(2ln2+1)γ/(γ−1)D(2ln2−1)γ/(γ+1)
The ratio of specific heats (Cp and Cv) for an ideal gas is γ. Volume of one mole sample of the gas is varied according to the law V=aT2 where T is temperature and a is a constant. Find the heat absorbed by the gas if its temperature changes by ΔT.
View SolutionAn ideal gas of adiabatic exponent γ, expands according to law PV= β (where β is the positive constant). For this process the compressibility of the gas is
View SolutionThe efficiency of an ideal gas with adiabatic exponent 'γ' for the shown cyclic process would be
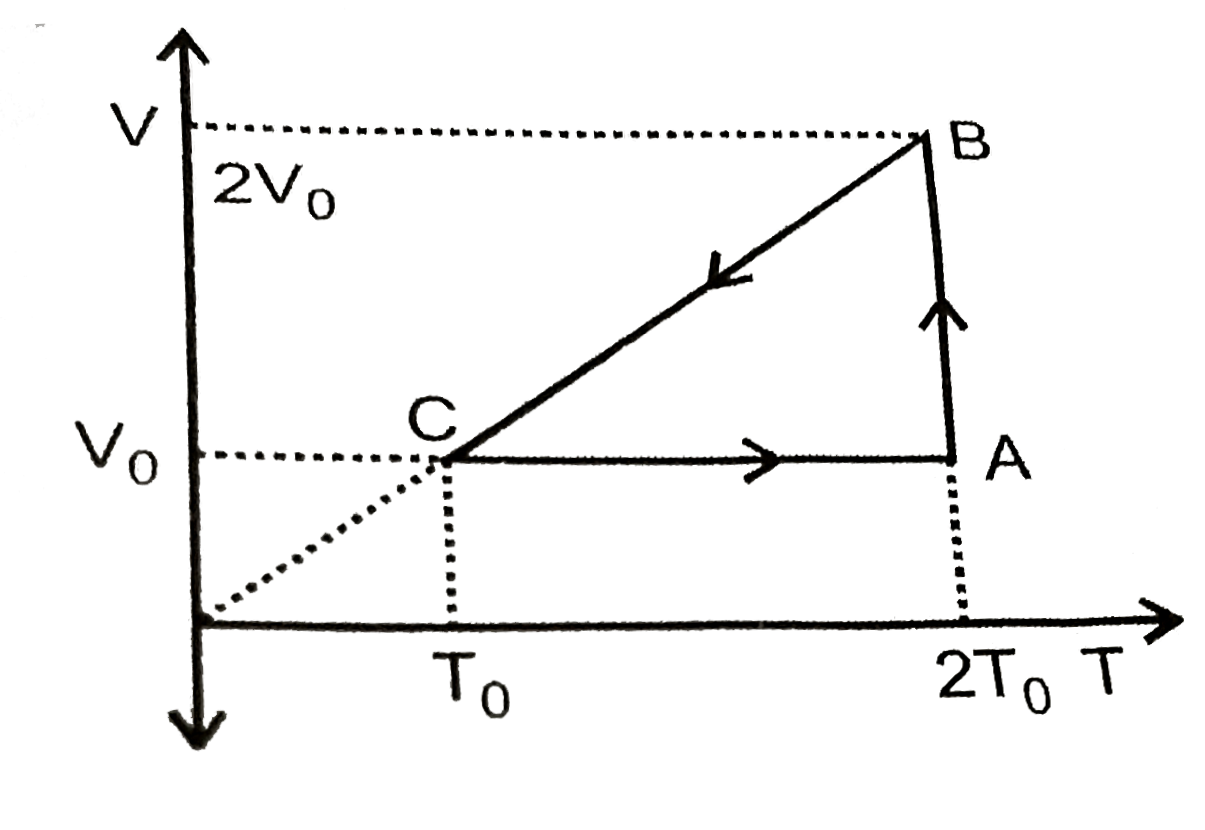
View SolutionIn a process, temperature and volume of one mole of an ideal monoatomic gas are varied according to the relation VT= K, where K is a constant. In this process the temperataure of the gas is increased by ΔT. The amount of heat absorbed by gas is (R is gas constant).
View SolutionAn ideal gas with adiabatic exponent γ is heated at constant pressure. It absorbs Q amount of heat. Fraction of heat absorbed in increasing the temperature is
View Solution
