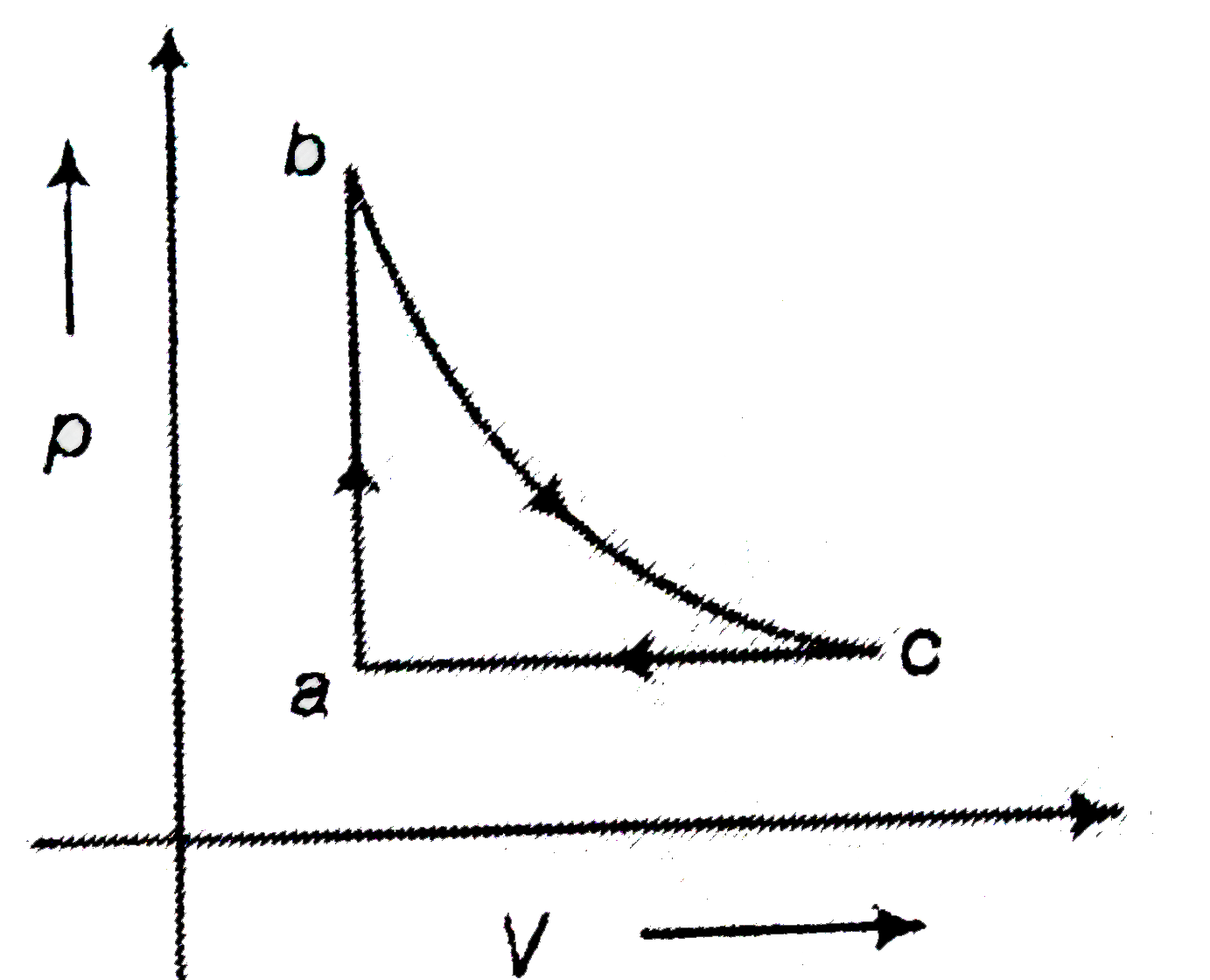
One mole of a monoatomic ideal gas is taken through the cycle ABCDA as shown in the figure.
TA=1000K and 2pA=3pB=6pC
![One mole of a monoatomic ideal gas is taken through the cycle ABCDA as shown in the figure. TA=1000K and 2pA=3pB=6pC [Ass um e(2/3)^0.4=0.85 and R=(25)/(3)JK^-1mol^-1] The temperature at B is](https://d10lpgp6xz60nq.cloudfront.net/physics_images/DCP_V03_CH21_E01_108_Q01.png)
[Assume(23)0.4=0.85 and R=253JK−1mol−1]
The temperature at B is
350K
1175K
850K
577K
The correct Answer is:C
In adiabatic process,
p1−γTγ=constant or T∝pγ−1γ
∴ TBTA=(pBpA)γ−1γ
∴ TB=(1000)(23)5/3−15/3
=(1000)(23)0.4=850K
Topper's Solved these Questions
- LAWS OF THERMODYNAMICSBook:DC PANDEYChapter:LAWS OF THERMODYNAMICSExercise:Level 2 Subjective
Explore 18 Videos
- LAWS OF THERMODYNAMICSBook:DC PANDEYChapter:LAWS OF THERMODYNAMICSExercise:Level 2 Passage I
Explore 2 Videos
- LAWS OF MOTIONBook:DC PANDEYChapter:LAWS OF MOTIONExercise:Medical entrances gallery
Explore 39 Videos
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBook:DC PANDEYChapter:MAGNETIC EFFECT OF CURRENT AND MAGNETISMExercise:Integer type Questions
Explore 10 Videos
Similar Questions
One mole of a monatomic ideal gas is taken through the cycle shown in the figure: A→B adiabatic expansion

B→C: cooling at constant volume
C→D adiabatic compression D→C: heating at constant volume.
The pressure and temperature at PA,PB etc. TA,TB etc. are denoted etc. respectively. Given that
TA=1000K,PB=(2/3)PA and PC=(1/3)PA
Calculate the following quantities.
The work done by the gas in process A→B (in J)
View SolutionOne mole of a monatomic ideal gas is taken through the cycle shown in the figure: A→B adiabatic expansion
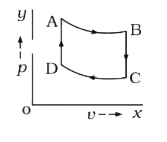
B→C: cooling at constant volume
C→D adiabatic compression D→A: heating at constant volume.
The pressure and temperature at PA,PB etc. TA,TB etc. are denoted etc. respectively. Given that
TA=1000K,PB=(2/3)PA and PC=(1/3)PA
Calculate the following quantities.
The temperature TD (in K) [Given : (25)2/5=0.85 ]
View Solution
Knowledge Check
One mole of a monoatomic ideal gas is taken through the cycle ABCDA as shown in the figure.
TA=1000K and 2pA=3pB=6pC

[Assume(23)0.4=0.85 and R=253JK−1mol−1]
Work done by the gas in the process A→B isA(a) 5312JB(b) 1875JC(c) 6251JD(d) 8854JOne mole of a monoatomic ideal gas is taken through the cycle ABCDA as shown in the figure.
TA=1000K and 2pA=3pB=6pC

[Assume(23)0.4=0.85 and R=253JK−1mol−1]
Heat lost by the gas in the process B→C isA(a) 5312JB(b) 1875JC(c) 6251JD(d) 8854J0.2 moles of an ideal gas is taken round the cycle ABC as shown in the figure. The path B→C is an adiabatic process A→B is an isochoric process and C→A is an isobaric process. The temperature at A and B are TA300K and TB=500k and pressure at A is 1 atm and volume at A is 4.91. The volume at C is
(given : γ=CPCV=53,R=8.205×10−2Latm mol−1K−1,(32)2/5=0.81)
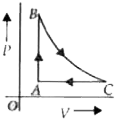 A6.9 LB6.6 LC5.5 LD5.8 L
A6.9 LB6.6 LC5.5 LD5.8 L
One mole of a monatomic ideal gas is taken through the cycle shown in the figure: A→B adiabatic expansion
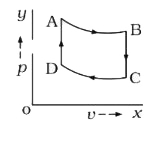
B→C: cooling at constant volume
C→D adiabatic compression D→C: heating at constant volume.
The pressure and temperature at PA,PB etc. TA,TB etc. are denoted etc. respectively. Given that
TA=1000K,PB=(2/3)PA and PC=(t/3)PA
Calculate the following quantities.
The heat lost by the gas in process B→C (in J)
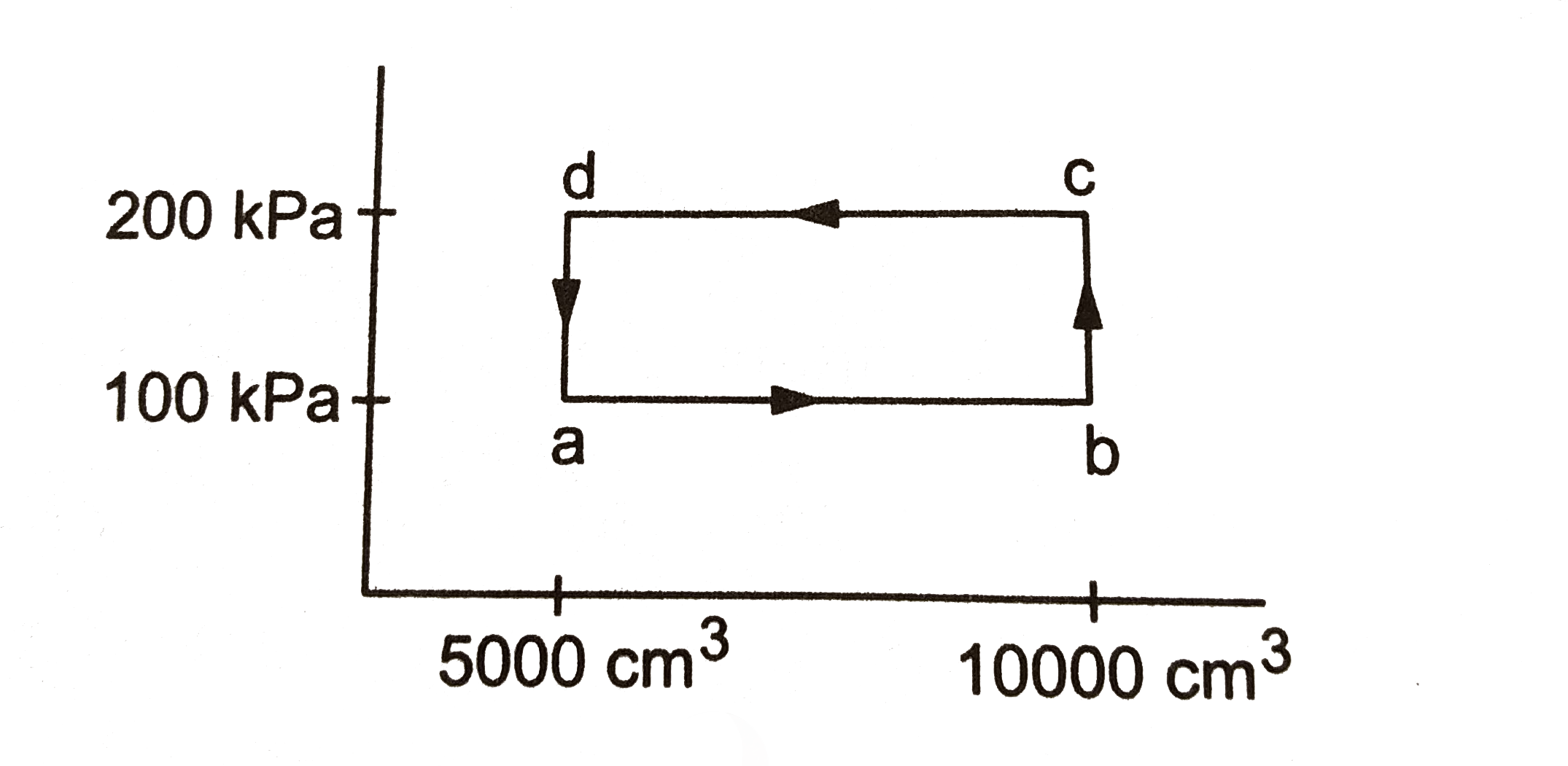
View SolutionHalf mole of an ideal gas (γ=53)istakenthroughthecyc≤abcdaasshown∈figure.Take(R = 25/3 JK^(-1) mol^(-1)).(a)F∈dthetemperatureofthegas∈thestaesa,b,candd.(b)F∈dtheamountofheat⊃plied∈theprocessesabandbc.(c)F∈dtheamountofheatliberated∈theprocessescd and da.
View SolutionOne mole of a monoatomic ideal gas is taken through the cycle shown in figure.
A→B Adiabatic expansion
B→C Cooling at constant volume
C→D Adiabatic compression.
D→A Heating at constant volume
The pressure and temperature at A,B etc., are denoted by pA,TA,pB,TB etc. respectively.
Given, TA=1000K, pB=(23)pA and pC=(13)pA. Calculate
(a) the work done by the gas in the process A→B
(b) the heat lost by the gas in the process B→C
Given, (23)0.4=0.85 and R=8.31J/mol−K
View SolutionOn mole of a monoatomic ideal gas is taken through the cycle shown in figure .
A→B : Adiabatic expansion B→C : Cooling at constant volume
C→D: Adiabatic compression D→A : Heating at constant volume
The pressure and temperature at A,B, etc, are denoted by PA,TA,PB,TB etc., respectively . Given that TA=1000K,PB=(23)PAandPC=(13)PA. Calculate the following quantities: (i) The work done by the gas in the processs A→B (ii) The heat lost by the gas in the process B→C (iii) The temperature TD.(Given:(23)2/5=0.85)
_E01_271_Q01.png)
View Solution0.2moles of an ideal gas, is taken around the cycle abc as shown in the figure. The path b-c is adiabatic process, a-b is isovolumic process and c-a is isobaric process. The temperature at a and b are TA=300K and Tb=500K and pressure at a is 1 atmospere. find the volume at c.
(Given, γ=CpCv=53,R=8.205×10−2L/atm/mol-K)
View Solution

