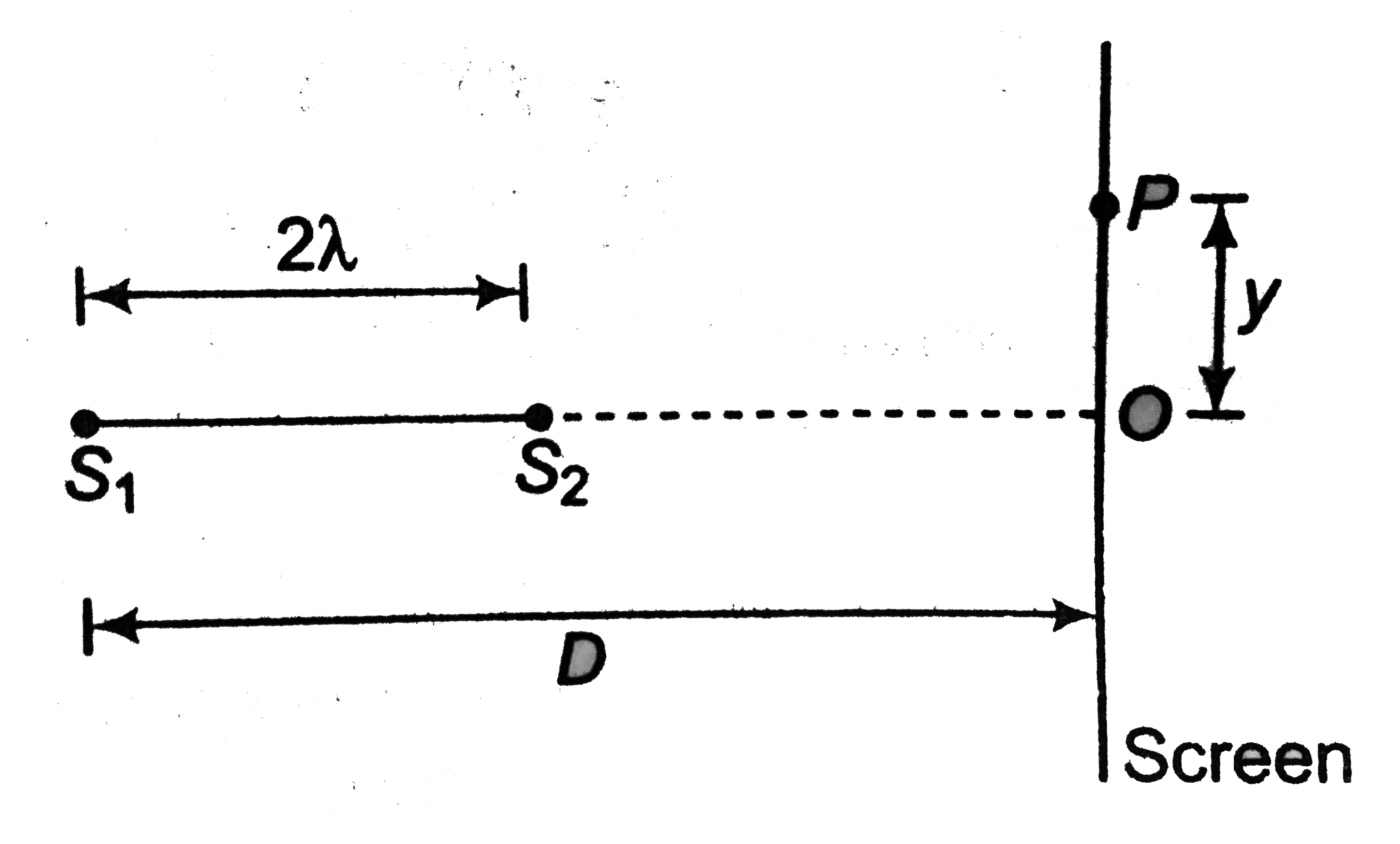
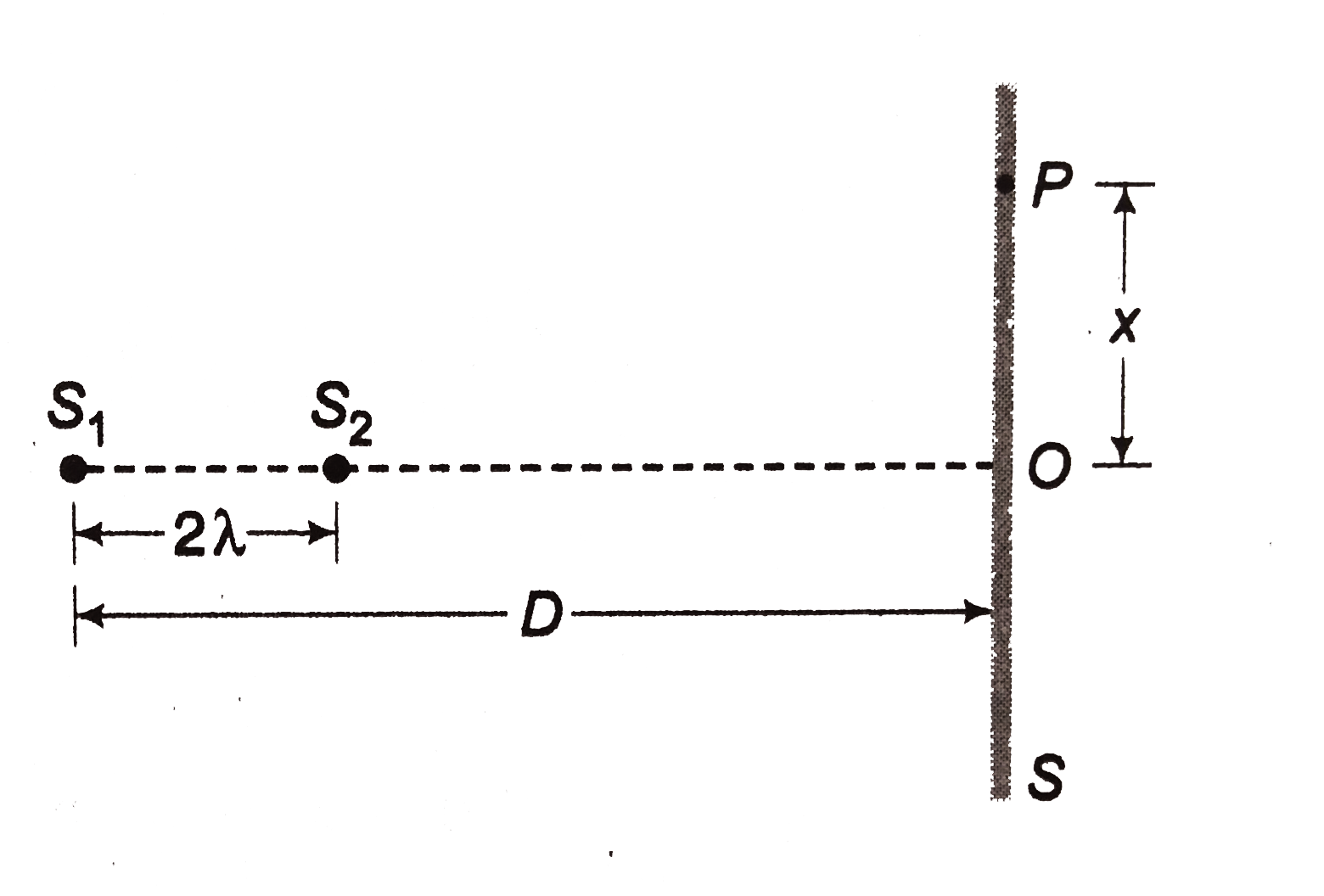
Two coherent narrow slits emitting sound of wavelength λ in the same phase are placed parallet to each other at a small separation of 2λ . The sound is delected by maving a delector on the screen at a distance D(>>λ) from the slit S1 as shows in figure. Find the distance y such that the intensity at P is equal to intensity at O .
The correct Answer is:C, D
At point O on the screen the path difference between the sound waves reaching from S1 and S1 is 2λ , i.e. constructive interference is obtained at O . At a very large distance from point O on the screen the path difference is zero.

Thus, we can conlude that as we move away from point O on the screen path difference decrease from 2λ at zero. At O constructive interference is obtained (where Δx=2λ) . So, next constructive interference will be obtained where Δx=λ . Hence,
S1P−S2P=λ
or √D2+y2−√y2+(D−2λ)2=λ
∴√D2+y2−λ=√y2+(D−2λ)2
On squaring both sides, we get
D2+y2+λ2−2λ√D2+y2=y2+D2+4λ2−4λD
∴2√D2+y2=4D−3λ
as D>>λ , 4D−3λ≈4D
∴2√D2+y2=4D
or √D2+y2=2D
Again squaring both sides, we get
D2+y2=4D2
or y=√(3)D
Let Δx=λ at angle theta as shows . Path difference between the waves is S1M=2λcosθ because S2P≈MP
:. 2λcosθ=λ
or θ=60∘(Δx=λ)
Now, PO=S1Otanθ=S1Otan60∘
or y=√(3)D
Topper's Solved these Questions
- SOUND WAVESBOOK - DC PANDEYCHAPTER - SOUND WAVESEXERCISE - Level 1 Assertion And Reason
10 Videos
- SOUND WAVESBOOK - DC PANDEYCHAPTER - SOUND WAVESEXERCISE - Level 1 Objective
34 Videos
- SOUND WAVESBOOK - DC PANDEYCHAPTER - SOUND WAVESEXERCISE - TYPE 5.
2 Videos
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBOOK - DC PANDEYCHAPTER - SOLVD PAPERS 2017 NEET, AIIMS & JIPMEREXERCISE - Solved paper 2018(JIPMER)
38 Videos
- SUPERPOSITION OF WAVESBOOK - DC PANDEYCHAPTER - SUPERPOSITION OF WAVESEXERCISE - Level 2 Subjective
8 Videos
Similar Questions
Two coherent narrow slits emitting sound of wavelength lamda in the same phase are placed parallel to each other at a small separation of 2λ. The sound is detected by moving a detector on the screen ∑ at a distance D(gtgtlamda) from the slit S1 as shown in figure. Find the distance x such that the intensity at P is equal to the intensity at O.
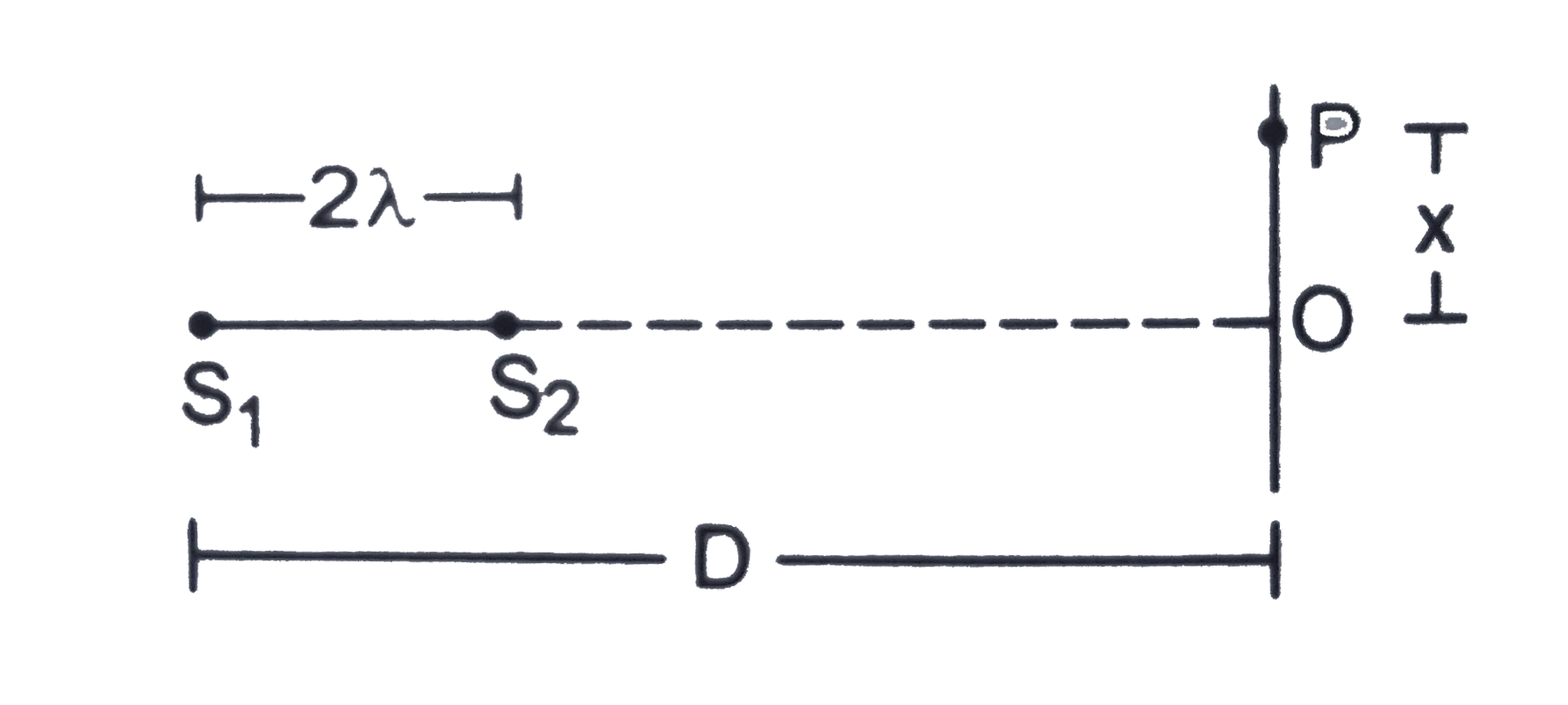
View SolutionTwo coherent narrow slits emitting wavelength λ in the same phase are placed parallel to each other at a small separation of 2λ, the sound is detected by moving a detector on the screen S at a distance D(>>λ) from the slit S1 as shown in Fig. 7.76. Find the distance x such that the intensity at P is equal to the intensity at O.

View Solution
Knowledge Check
_E01_037_Q01.png)
Two coherent narrow slits emitting light of wavelength λ in the same phase are placed parallel to each other at a small separation of 3λ the light is collected on a screen S which is placed at a distance D(>>λ) from the slits the smallest distance x such that the P is a maxima.A√3DB√8DC√5DD√5D2Choose the most appropriate option.
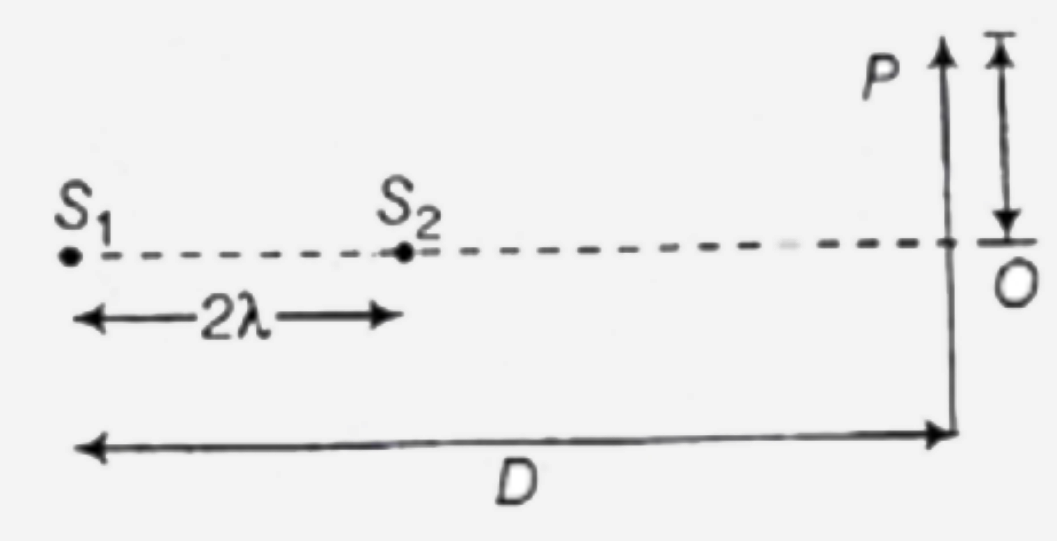
Two coherent point sources S1andS2 vibrating in phase emit light of wavelength λ. The separation between them is 2λ. The light is collected ona screen placed at a distance D>>λ from the slit S1 as shown. The minimum distance, so that intensity at P is equal to intensity at O.
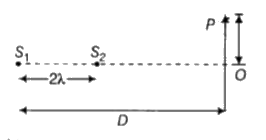 A√2DB√3DC√8DD√5D
A√2DB√3DC√8DD√5DTwo coherent sources A & B emitting light of wavelength lambda are placed at position (-D,0) and (−D,3λ) respectively Here D >>λ The number of minima on y-axis and maxima on x-axis respectively are
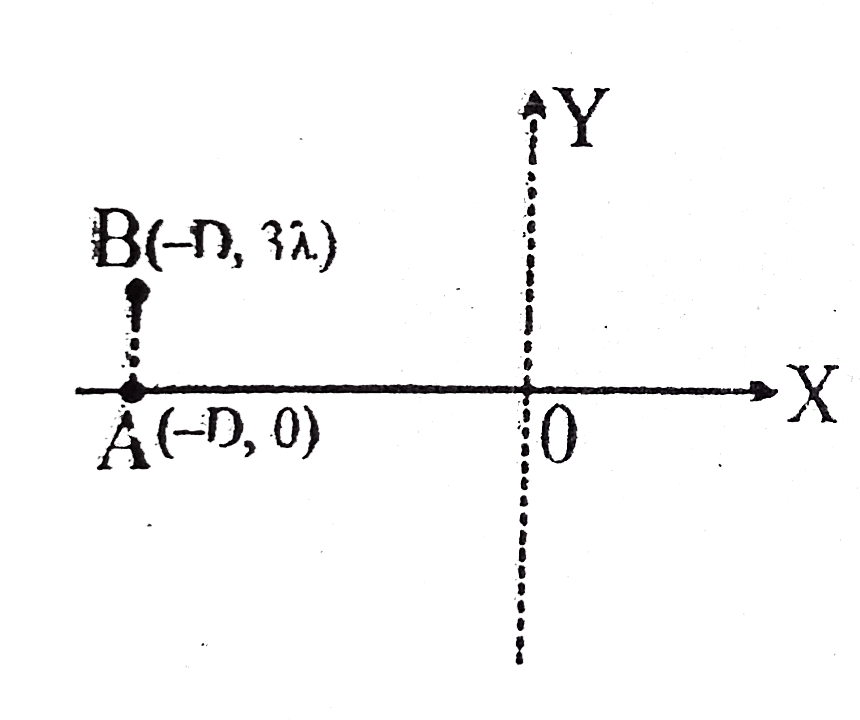 A6,5B5,6C4,3D3,4
A6,5B5,6C4,3D3,4
Two coherent narrow slits emitting light of wavelength λ in the same phase are placed parallel to each other at a small separation of 2λ. The light is collected on a screen S which is placed at a distance D(gtgtλ) from the slit S1 as shown in figure. Find the finite distance x such that the intensity at P is equal to intensity O.
 .
.
View SolutionTwo coherent point sources S1andS2 vibrating in phase emit light of wavelength λ . The separation between them is 2λ . The light is collected on a screen placed at a distance D>>λ from the slit S1 as shown. The minimum distance, so that intensity at P is equal to the intensity at O
View SolutionConsider two coherent, monochromatic (wavelength λ) sources S1andS2, separated by a distance d. The ratio of intensities of S1 and that of S2 (which is responsible for interference at point P, where detector is located) is 4. The distance of point P from S1 is (if the resultant intensity at point P is equal to 94 times of intensity of S1) (Given : ∠S2S1P=90∘,d>0andn is a positive integer)
View SolutionA coherent parallel beam of microwaves of wavelength λ=0.5mm falls on aYoung's double- slit apparatus. The separation between the slits is 1.0 mm. The intensity of microwaves is measured on a screen placed parallel to the plane of the slits at a distance of 1.0 m from it as shown in figure
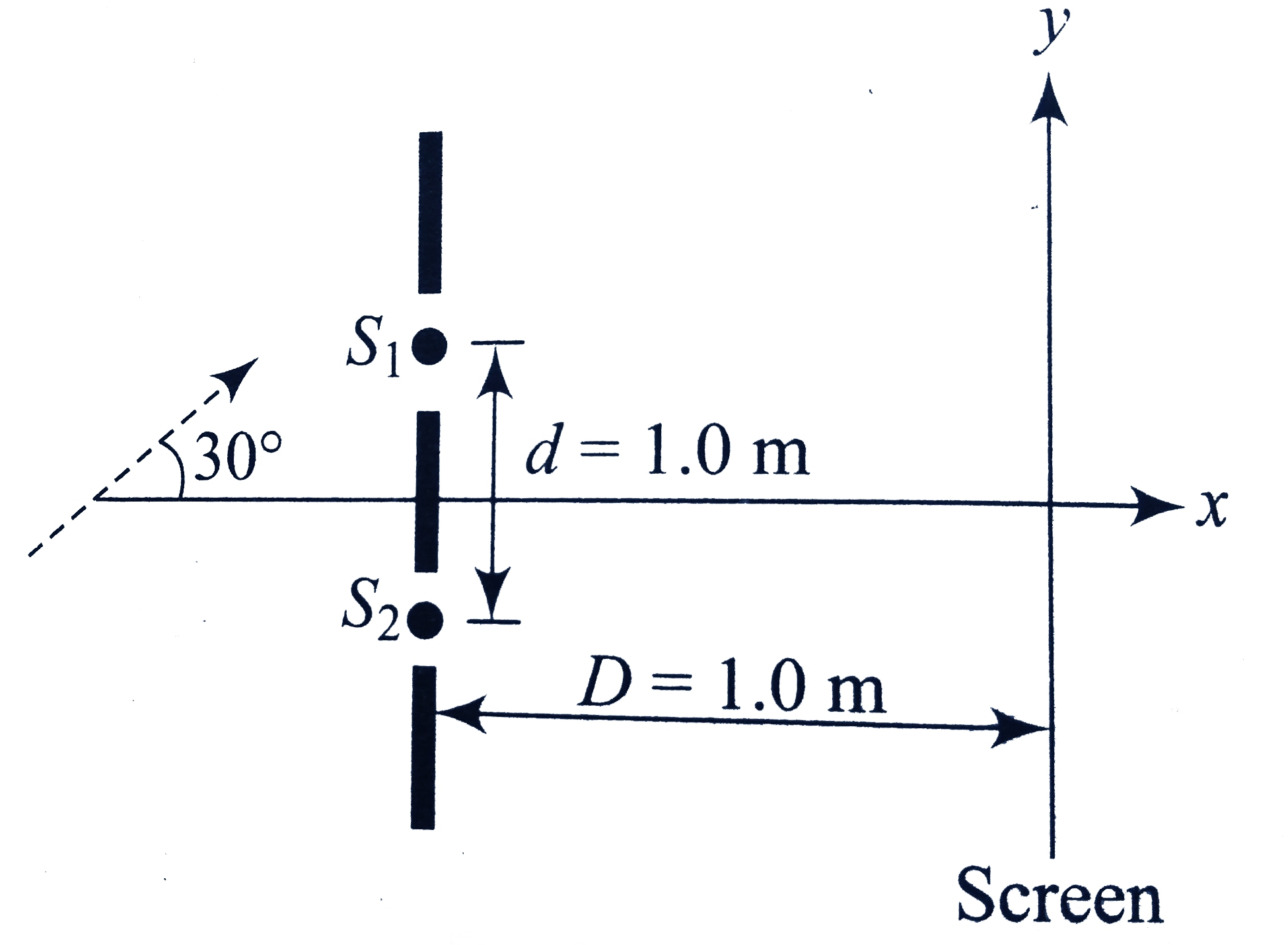
If the incient beam falls normally on the double-slit apparatus, find the order of the interference minima on the screen
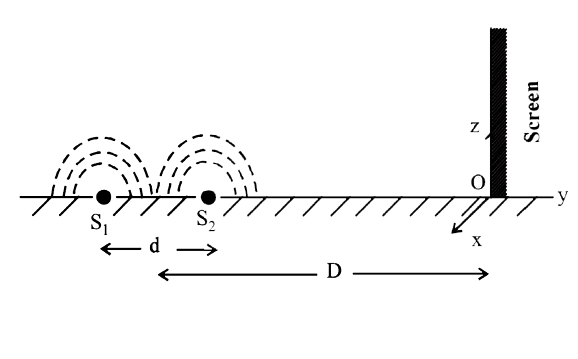
View SolutionWhile conduction the Young's double slit experiment, a student replaced the two slits with a large opaque plate in the x-y plane containing two small holes that act as two coherent point sources (S1,S2) emitting light of wavelength 600nm. The student mistakenly placed the screen parallel to the x-z plane (forz>0) at a distance D=3 m from the mid-point of S1,S2, as shown schematically in the figure. The distance between the sources d=0.6003mm. The origin O is at the intersection of the screen and the line joining S1S2. Which of the following is (are) true of the intensity pattern of the screen?
View Solution
