Transverse waves on a srting have speed 12.0m/s, amplitude 0.05m and wavelength 0.4m. The waves travel in the +x−direction and at t=0 the x=0 end of the string has zero displacement and is moving upwards.
(a) Write a wave function describing the wave.
(b) Find the transverse displacement of a point at x=0.25m at time t=0.15s.
( c ) How much time must elapse from the instant in part (b) until the point at x=0.25m has zero dispacement?
The correct Answer is:A, B, C, D
(a) ω=2πf=2π(vλ)=2π(120.4)
=(60π)rad/s
k=2πλ=2π0.4=(5π)m−1
Since, wave is travelling along +ve x-direction, ωtandkx should have opposite sign. Further at t=0,x=0 the string has zero displacement and moving upward (in positive cirection). Hence at x=0, we should have Asinωt not −Asinωt. Therefore, the correct expression is
yAsin(ωt−kx)
or y=0.05sin(60πt−5πx)
(b) Putting x=0.2m and
t=0.15s in above equation we have, y=−0.0354m
=−3.54cm
( c ) In part (b), y=A/√2
From y=A√2 to y=0, time taken is
t=T8=2πω×8
=2π(60π)(8)
=4.2×10−3s
=4.2ms
Topper's Solved these Questions
- WAVE MOTIONBook:DC PANDEYChapter:WAVE MOTIONExercise:Level 2 Single Correct
Explore 5 Videos
- WAVE MOTIONBook:DC PANDEYChapter:WAVE MOTIONExercise:Level 2 More Than One Correct
Explore 6 Videos
- WAVE MOTIONBook:DC PANDEYChapter:WAVE MOTIONExercise:Level 1 Objective
Explore 6 Videos
- VECTORSBook:DC PANDEYChapter:VECTORSExercise:Medical enrances gallery
Explore 9 Videos
- WORK, ENERGY & POWERBook:DC PANDEYChapter:WORK, ENERGY & POWERExercise:Level 2 Comprehension Based
Explore 2 Videos
Similar Questions
A wave travels along the positive x-direction with a speed of 20ms−1. The amplitude of the wave is 0.20 cm and the wavelength 2.0 cm. (a) Write a suitable wave equation which describes this wave. (b) What is the displacement and velocity of the particle at x = 2.0 cm at time t = 0 according to the wave equation written ? Can you get different values of this quantity if the wave equation is written in a different fashion ?
View SolutionA wave propagates on a string in the positive x-direction at a velocity u. The shape of the string at t=t0 is given by g(x,t0)=Asin(xa) . Write the wave equation for a general time t.
View Solution
Knowledge Check
A transverse wave, whose amplitude is 0.5 m wavelength is 1 m and frequency is 2Hz. is travelling along positive x direction. The equation of this wave will be-
Ay=0.5cos(2πx−4πt)By=0.5cos(2πx−4πt)Cy=0.5sin(πx−2πt)Dy=0.5cos(2πx−2πt)A wave in a string has an amplitude of 2cm. The wave travels in the +ve direction of x axis with a speed of 128ms−1 and it is noted that 5 complete waves fit in 4m length of the string. The equation describing the wave is
Ay=(0.02)msin(15.7x−2010t)By=(0.02)msin(15.7+2010t)Cy=(0.02)msin(7.85x−1005t)Dy=(0.02)msin(7.85x+1005t)A transverse wave of amplitude 0.5m and wavelength 1 m and frequency 2 Hz is propagating in a string in the negative x - direction. The expression for this wave is
Ay(x,t)=0.5sin(2πx−4πt)By(x,t)=0.5cos(2πx+4πt)Cy(x,t)=0.5sin(πx−2πt)Dy(x,t)=0.5cos(2πx+2πt)
The speed of a transverse wave on a string is 450 m/s, and the wavelength is 0.18 m. The amplitude of the wave is 2.0 mm. How much time is required for a particle of the string to move through a total distance of 1.0 km?
View SolutionA transverse wave of amplitude 0.5m and wavelength 1 m and frequency 2 Hz is propagating in a string in the negative x - direction. The expression for this wave is [
View SolutionA transverse sinusoidal wave of wavelength 20 cm is moving along a string towards increasing x. the transverse displacement of the string particle at x=0 as a function of time is shown in figure.
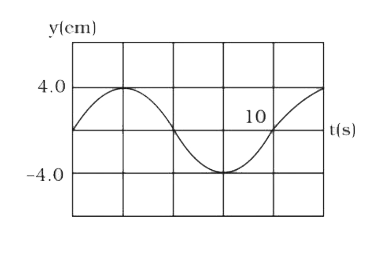
Q. Skecth of one wavelength of the wave (the portion between x=0 and x=20cm) at time t=0 is:
View SolutionA transverse sinusoidal wave of wavelength 20 cm is moving along a string towards increasing x. the transverse displacement of the string particle at x=0 as a function of time is shown in figure.
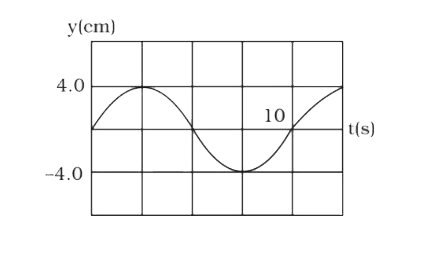
Q. The velocity of propagation of the wave is ?
View SolutionA transverse sinusoidal wave of wavelength 20 cm is moving along a string towards increasing x. the transverse displacement of the string particle at x=0 as a function of time is shown in figure.
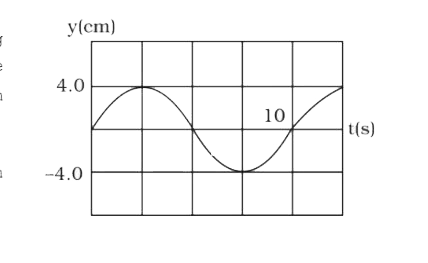
Q. The transverse velocity of the particle at x=0 at t=5.0 s is ?
View Solution

