In the shown arrangement, both the spring are in their natural lengths. The coefficient of friction between m2 and m1 is μ. There is no friction between m1 and the surface. If the blocks are displaced slightly, they together perform simple harmonic motion. Obtain

(a) Frequency of such oscillations.
(b) The condition if the friction force on clock m2 is to act in the direction of its displacement from mean position.
( c) If the condition obtained in (b) is met, what can be maximum of their oscillations ?
The correct Answer is:A, B, C
(a) f=12π√Kefftotal mass=12π√k1+k2m1+m2
(b) Suppose the system is displaced towards left by a distance x.
Restoring force on m1 :

F=m1ω2x (towards right)
=m1(k1+k2m1+m2)x
Friction f on it will be towards right if,
k1x<F
or k1x<m1(k1+k2m1+m2)x
or k1k2<m1m2
( c) k1Am+μm2g=m1(k1+k2m1+m2)Am
Am(m1k1+m1k2m1+m2−k1)=μm2g
or Am=μ(m1+m2)m2gm1k2−m2k1
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEYCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise 14.1
5 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEYCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Intro. Exer.
1 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEYCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Level 2 Comprehension
2 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBOOK - DC PANDEYCHAPTER - SEMICONDUCTORS AND ELECTRONIC DEVICESEXERCISE - More than One Option is Correct
3 Videos
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBOOK - DC PANDEYCHAPTER - SOLVD PAPERS 2017 NEET, AIIMS & JIPMEREXERCISE - Solved paper 2018(JIPMER)
38 Videos
Similar Questions
(i) In the shown arrangement, both springs are relaxed. The coefficient of friction between m2 and m1 is μ. There is no friction between m1 and the horizontal surface. The blocks are displaced slightly and released. They move together without slipping on each other.
(a) If the small displacement of blocks is x then find the magnitude of acceleration of m2. What is time period of oscillations ?
(b) Find the ratio m1m2 so that the frictional force on m2 acts in the direction of its displacement from the mean position.
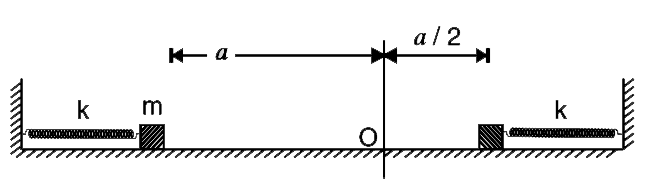
(ii) Two small blocks of same mass m are connected to two identical springs as shown in fig. Both springs have stiffness K and they are in their natural length when the blocks are at point O. Both the blocks are pushed so that one of the springs get compressed by a distance a and the other by a/2. Both the blocks are released from this position simultaneously. Find the time period of oscillations of the blocks if - (neglect the dimensions of the blocks)
(a) Collisions between them are elastic.
(b) Collisions between them are perfectly inelastic.
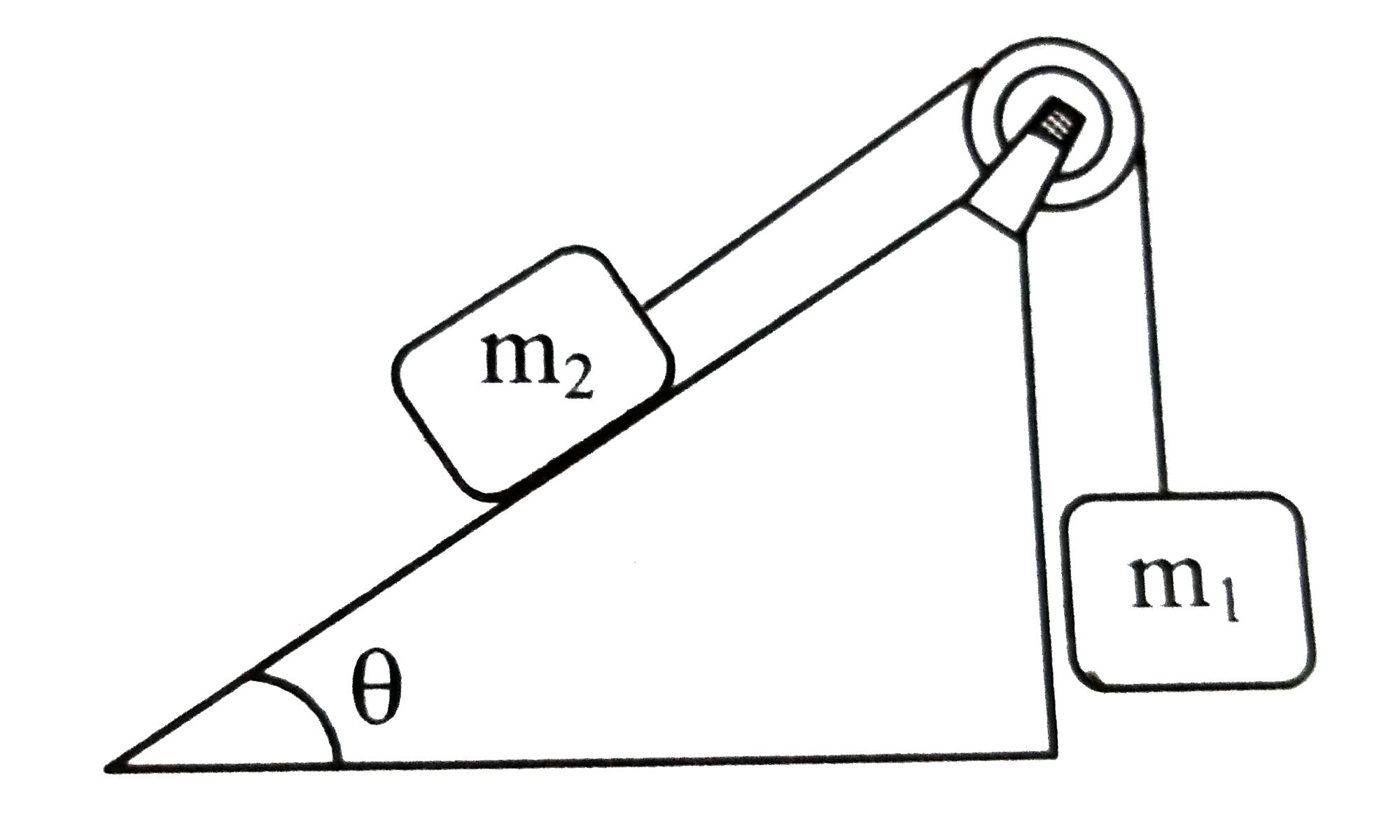
View SolutionThe coefficient of friction between m2 and inclined plane is μ (shown in the figure). If m1m2=sinθ then
View Solution
Knowledge Check
In the arrangement shown in figure, coefficient of friction between the two blocks is μ=1/2. The force of friction acting between
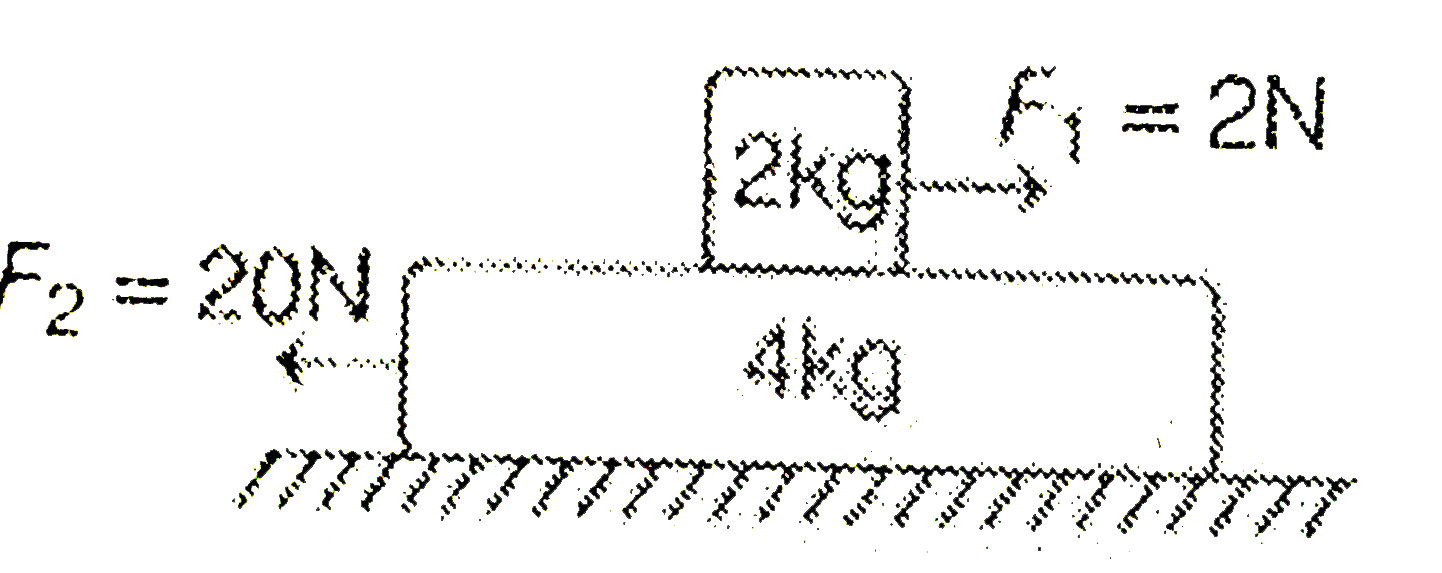 A8NB10NC6ND4N
A8NB10NC6ND4NThe coefficient of friction between the block A of mass m & block B of mass 2m is μ. There is no friction between A&B is released from rest & there is no slipping between A&B then:
 A2θ≤sin−1(2μ)Bθ≤tan−1(μ)C2θ≤cos−1(2μ)D2θ≤tan−1(μ/2)
A2θ≤sin−1(2μ)Bθ≤tan−1(μ)C2θ≤cos−1(2μ)D2θ≤tan−1(μ/2)A mass m rests under the action of a force F as shown in the figure-2.158 on a horizontal surface. The coefficient of friction between the mass and the surface is μ. The force of friction between the mass and the surface is :
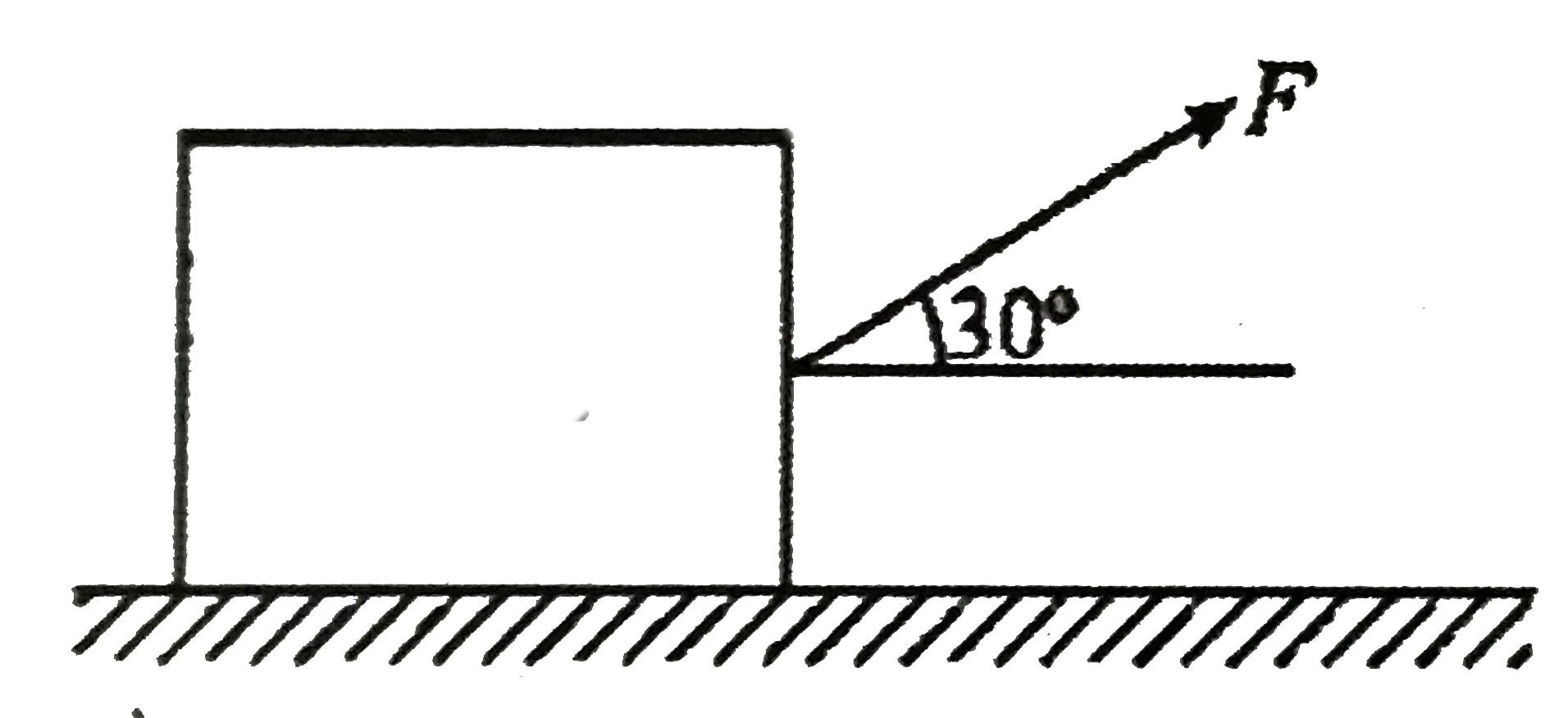 AμmgBμ[mg+F2]CF√32Dμ[mg−F2]
AμmgBμ[mg+F2]CF√32Dμ[mg−F2]
The coefficient of friction between the block A of mass m and the triangular wedge B of mass M is μ. There in no friction between the wedge and the plane if the system (block A+ wedge B) is released so that there is no stiding between A and B find the inclination θ

View SolutionIf coefficient of friction between both the block is μ−12 . Find friction force acting between both block.
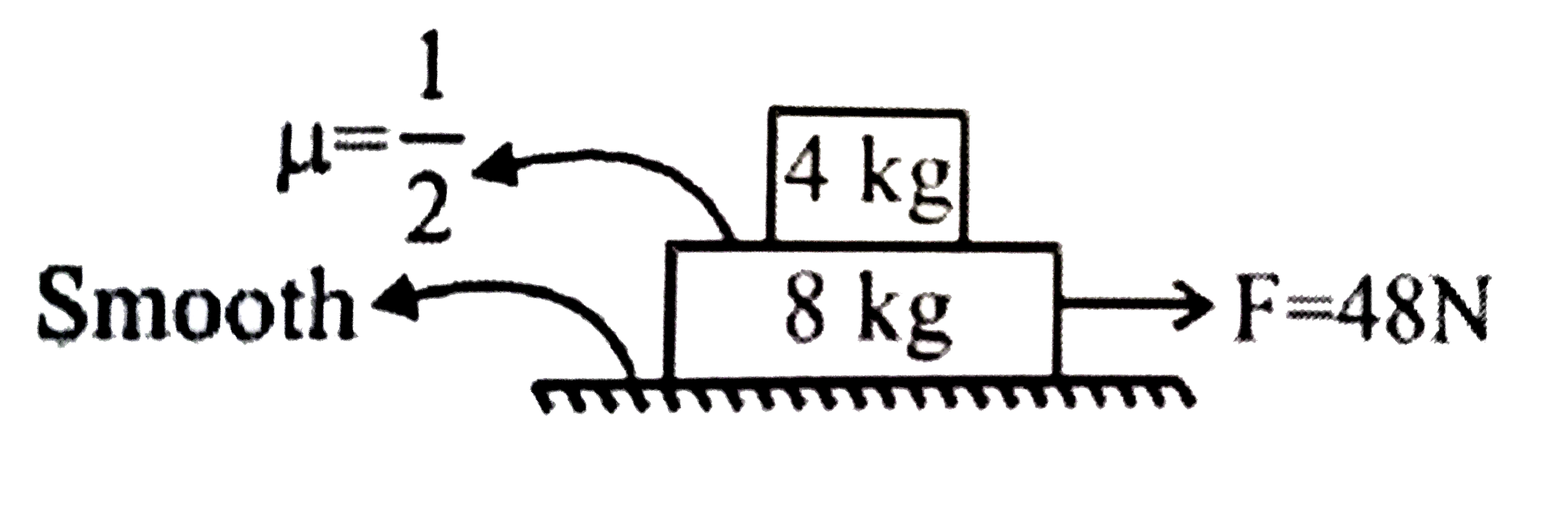
View SolutionA pendulum of mass m and length L is connected to a spring as shown in figure. If the bob is displaced slightly from its mean position and released, it performs simple harmonic motion. The angular frequency of the oscillation of bob is
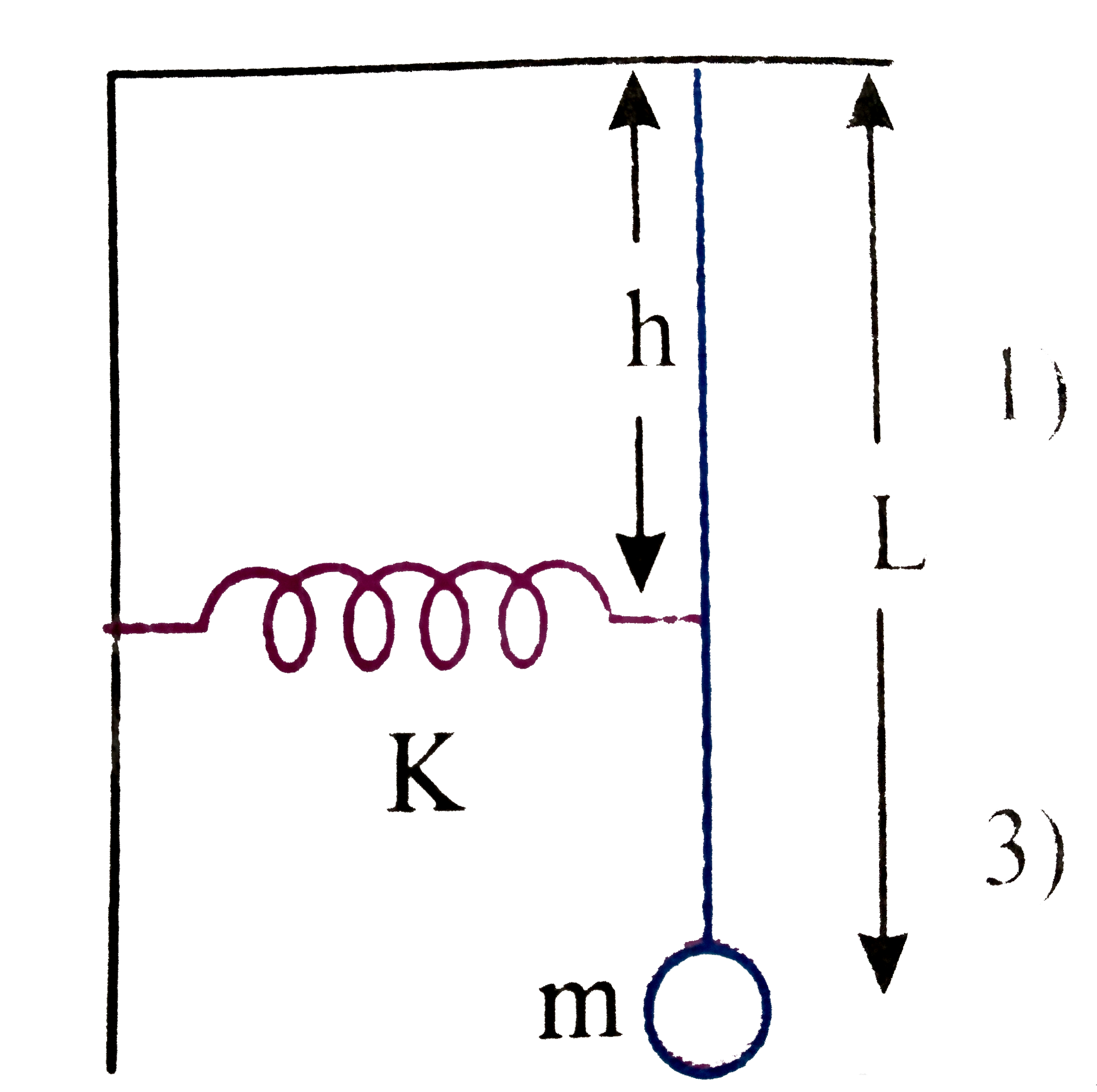
View Solution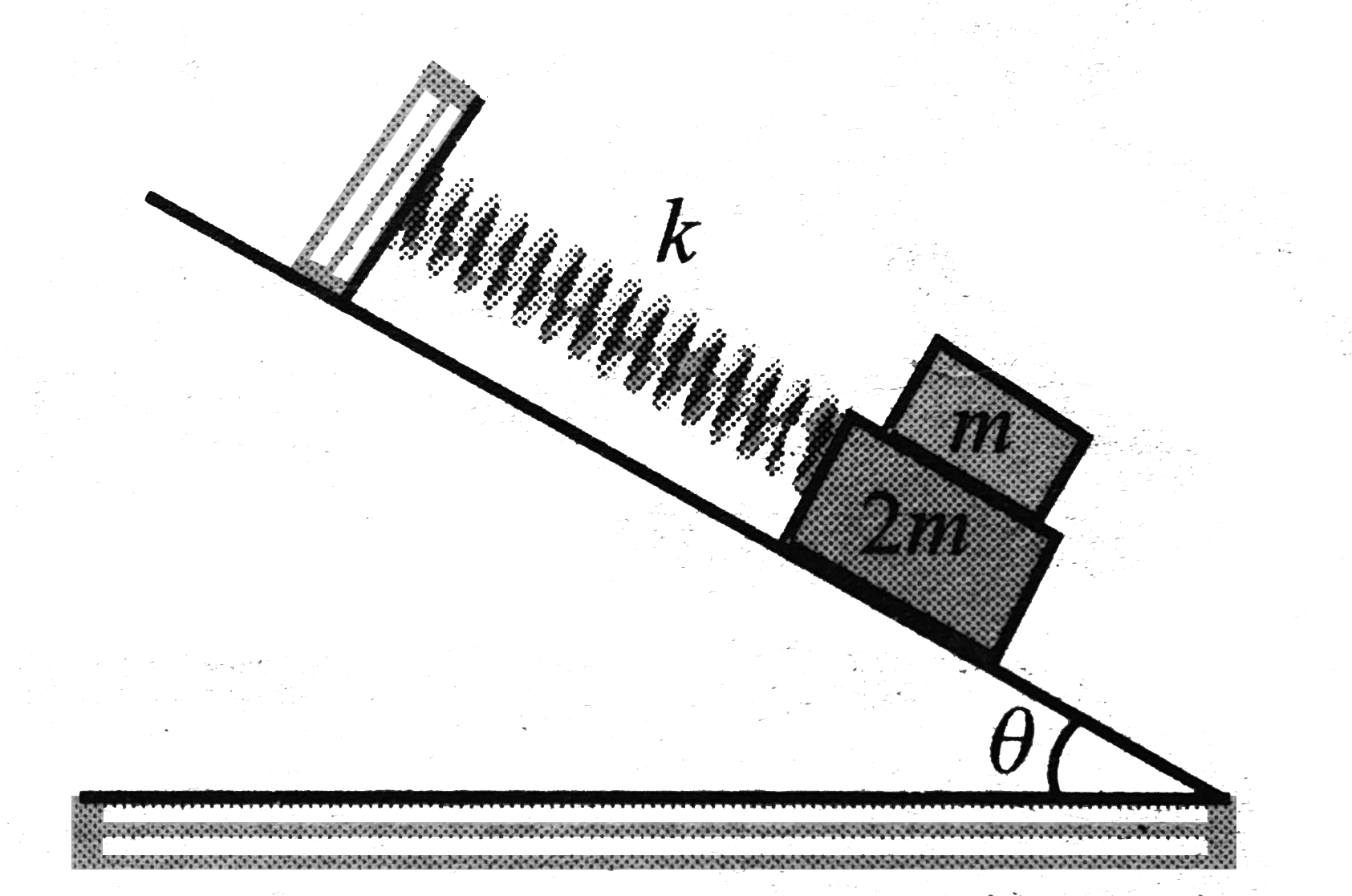
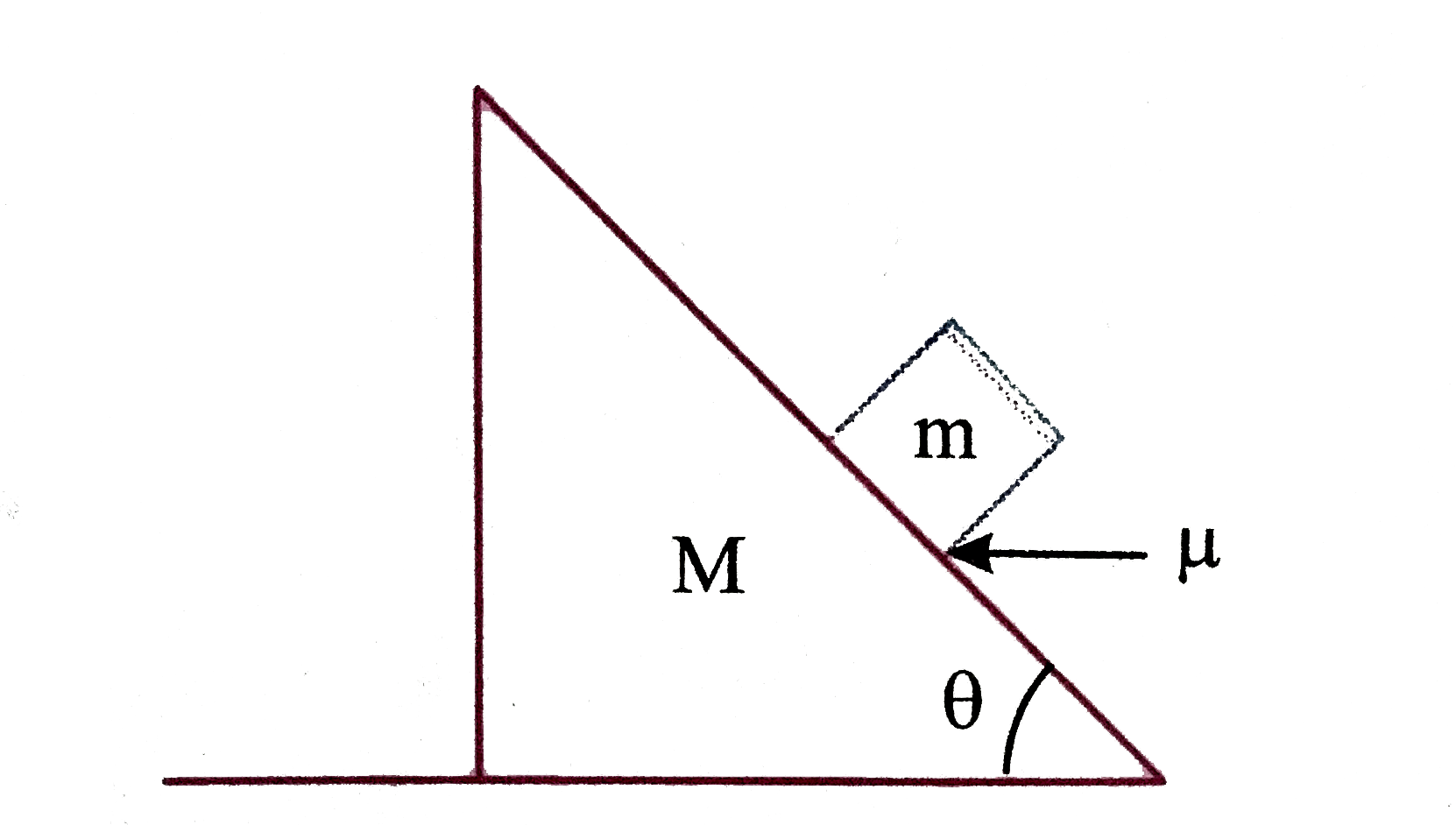
The coefficient of friction between block of mass m and 2m is μ=2tanθ. There is no friction between block of mass 2 m and inclined plane. The maximum amplitude of the two block system for which there is no relative motion between both the blocks is
View SolutionCalculate angle of friction between wedge and block system is at rest M coefficient of friction between wedge and block.
View Solution
