A 2kg mass is attached to a spring of force constant 600N/m and rests on a smooth horizontal surface. A second mass of 1kg slides along the surface toward the first at 6m/s.
(a) Find the amplitude of oscillation if the masses make a perfectly inelastic collision and remain together on the spring. what is the period of oscillation ?
(b) Find the amplitude and period of oscillation if the collision is perfectly elastic.
( c) For each case , write down the position x as a function of time t for the mass attached to the spring, assuming that the collision occurs at time t=0. What is the impulse given to the 2kg mass in each case ?
The correct Answer is:A, B, C, D
(a) ω=√km=√6002+1=10√2rad/s
From conservation of liner momentum (at mean position) velocity of combined mass will be 2m/s.
This is the maximum velocity of combined mass.
∴v=ωA
or A=vω=210√2m
=0.141m=14.1cm
T=2πω=2π10√2=0.44s
(b) If the collision is elastic,
ω'=√6002=10√3rad/s
In elastic collision,
v'2=(m2−m1m2+m1)v2+(2m1m1+m2)v1
=(2×11+2)(6)=4m/s (As v2=0)
This is maximum velocity.
∴v'2=ω'A'
or A'=v'2ω'=410√3
=0.23m=23cm
T'=2πω'=2π10√3=0.36s
( c) In both cases journey is started from mean position
∴x=±Asinωt
will be the displacement - time eqution. For impulse we can apply the equation. Impulse = change in liner momentum.
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEYCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise 14.1
5 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEYCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Intro. Exer.
1 Video
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEYCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Level 2 Comprehension
2 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBOOK - DC PANDEYCHAPTER - SEMICONDUCTORS AND ELECTRONIC DEVICESEXERCISE - More than One Option is Correct
3 Videos
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBOOK - DC PANDEYCHAPTER - SOLVD PAPERS 2017 NEET, AIIMS & JIPMEREXERCISE - Solved paper 2018(JIPMER)
38 Videos
Similar Questions
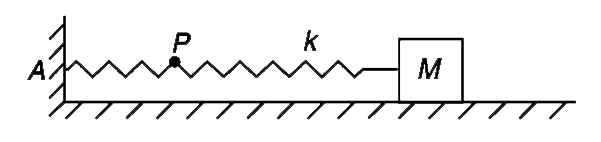
A block of mass M is tied to a spring of force constant k and placed on a smooth horizontal surface. The natural length of the spring is L. P is a point on the spring at a distance L4 from its fixed end. The block is set in oscillations with amplitude A. Find the maximum speed of point P on the spring.
View Solution
The period of oscillation of a mass M suspended from a spring of spring constant K is T. the time period of oscillation of combined blocks is
View Solution
Knowledge Check
A 1 kg mass is attached to a spring of force constant 600 N/m and rests on a smooth horizontal surface with other end of the spring tied to wall as shown in figure. A second mass of 0.5 kg slides along the surface towards the first at 3m/s. If the masses make a perfectly inelastic collision, then find amplitude and time period of oscillation of combined mass.
 A5cm,π10sB5cm,π5sC4cm,2π5sD4cm,π3s
A5cm,π10sB5cm,π5sC4cm,2π5sD4cm,π3sThe graph between period of oscillation (T) and mass attached (m) to a spring will be
A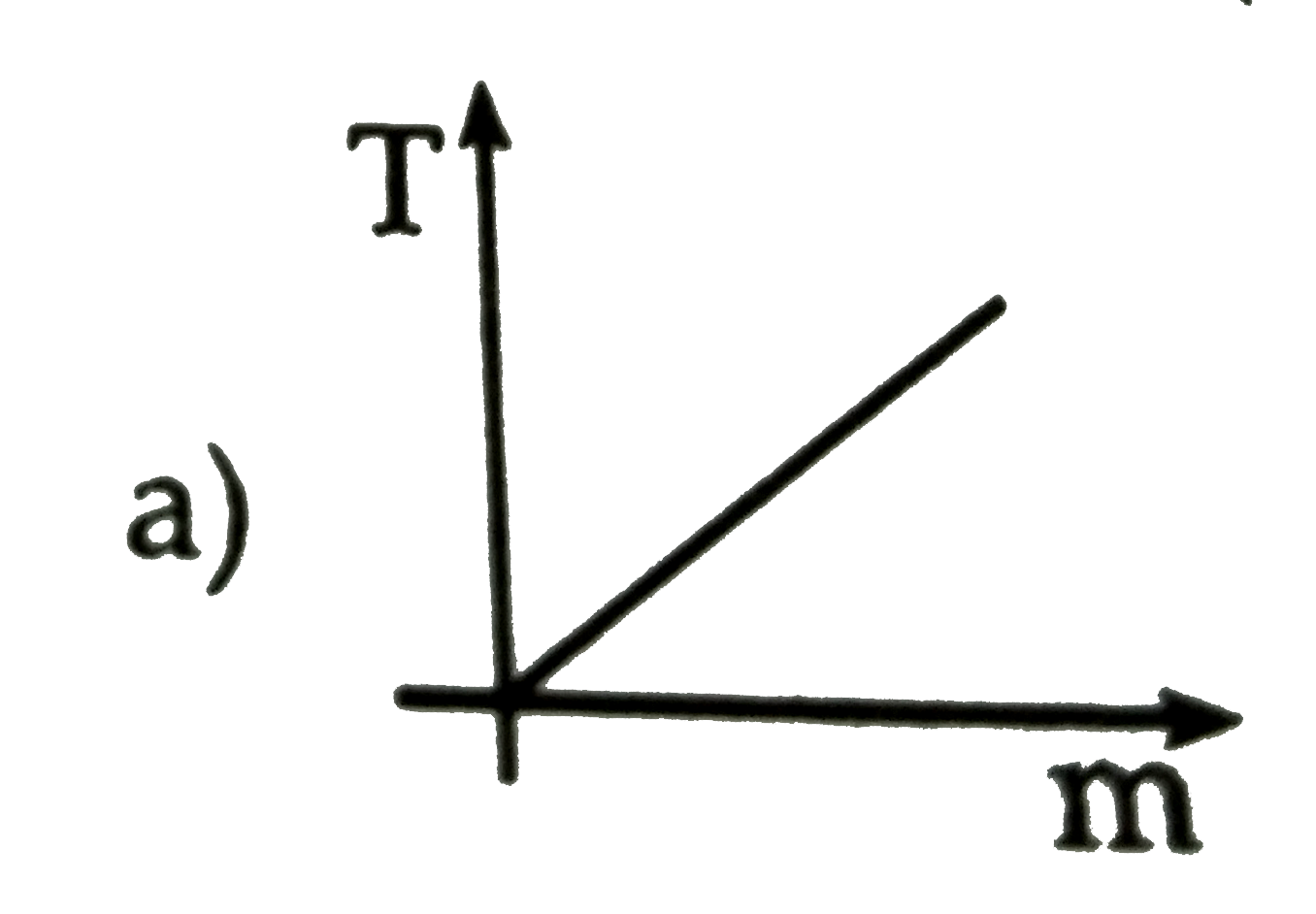 B
B C
C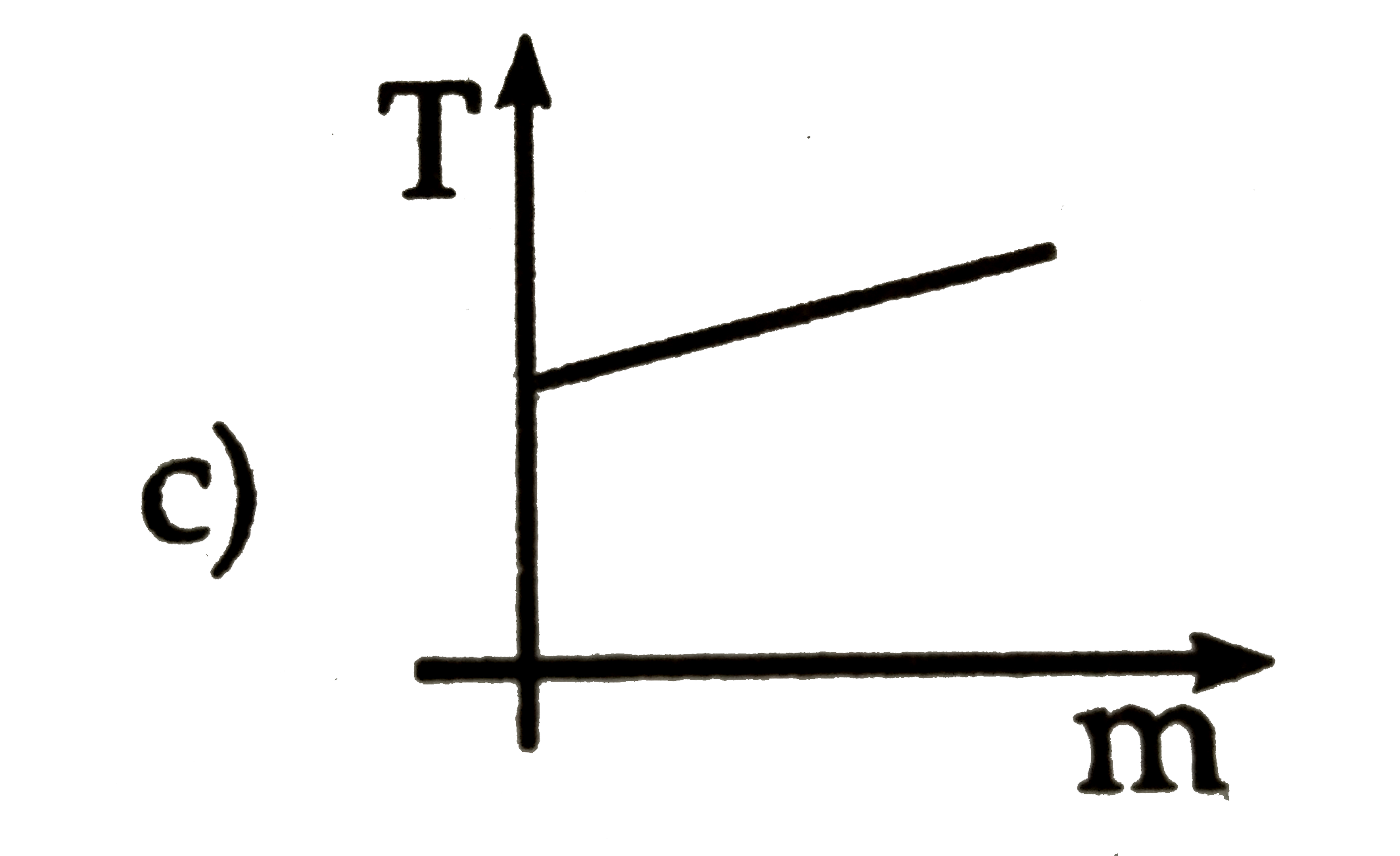 D
D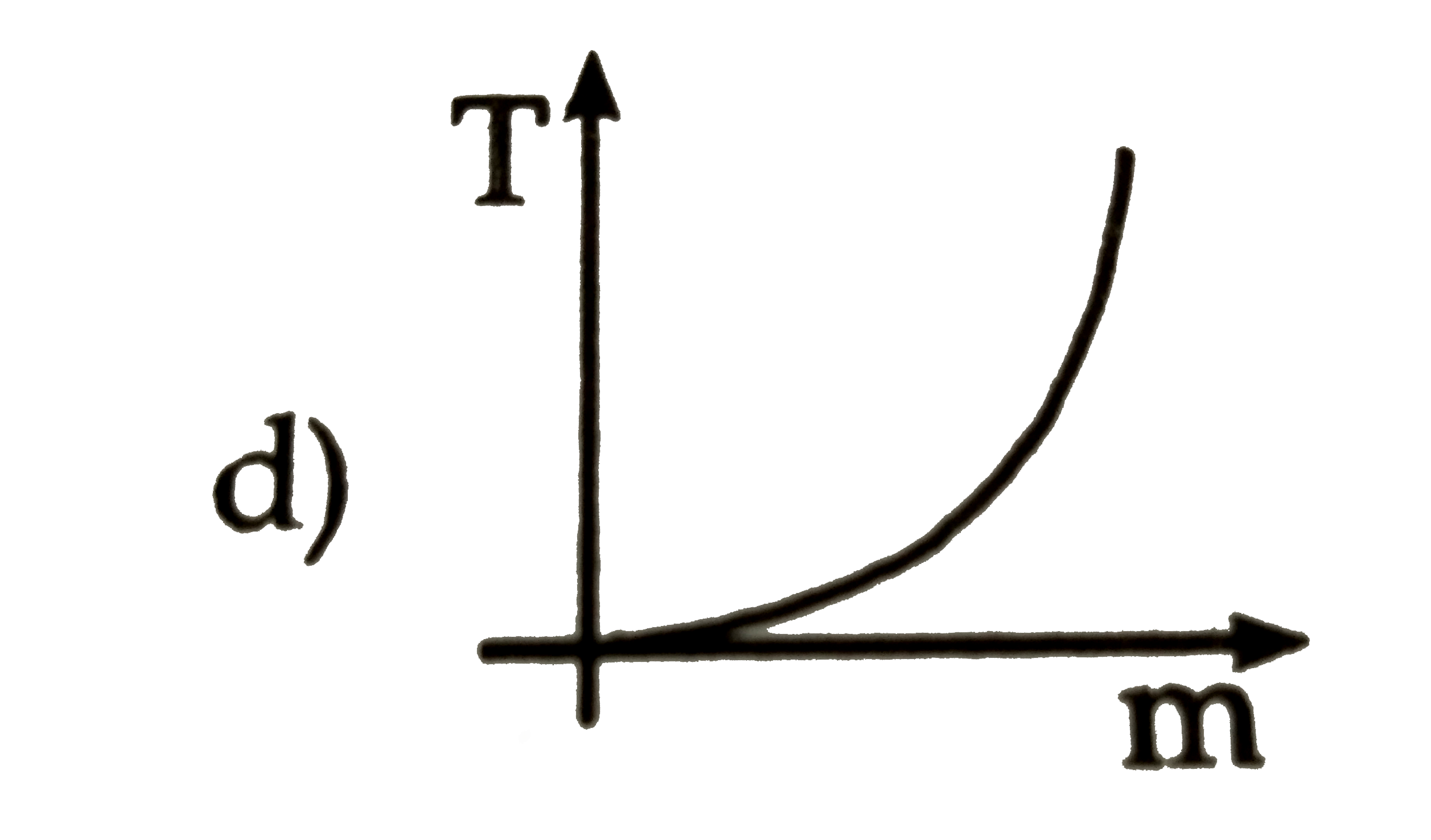
a block of mass 0.1 kg attached to a spring of spring constant400Nm pulled horizontally from x=0 tox1=10mm. Find the work done by the spring force
A2⋅10−2JB2⋅10−6JC3⋅10−6JD4⋅10−2J
A block of mass 'm' is attached to the light spring of force constant K and released when it is in its natural length. Find amplitude of subsequent oscillations.
View SolutionA body of mass 1 kg oscillates on a spring of force constant 16 N/m. Calculate the angular frequency.
View SolutionA block of mass 0.2 kg is attached to a mass less spring of force constant 80 N/m as shown in figure. Find the period of oscillation. Take g=10m/s2. Neglect friction

View SolutionCalculate the period of oscillations of block of mass m attached with a set of springs as shown
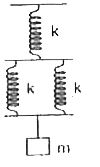
View SolutionA mass M is attached to a horizontal spring of force constant k fixed one side to a rigid support as shown in figure. The mass oscillates on a frictionless surface with time period T and amplitude A. When the mass M is in equilibrium position, another mass m is gently placed on it. When will be the new amplitude of ocillation?
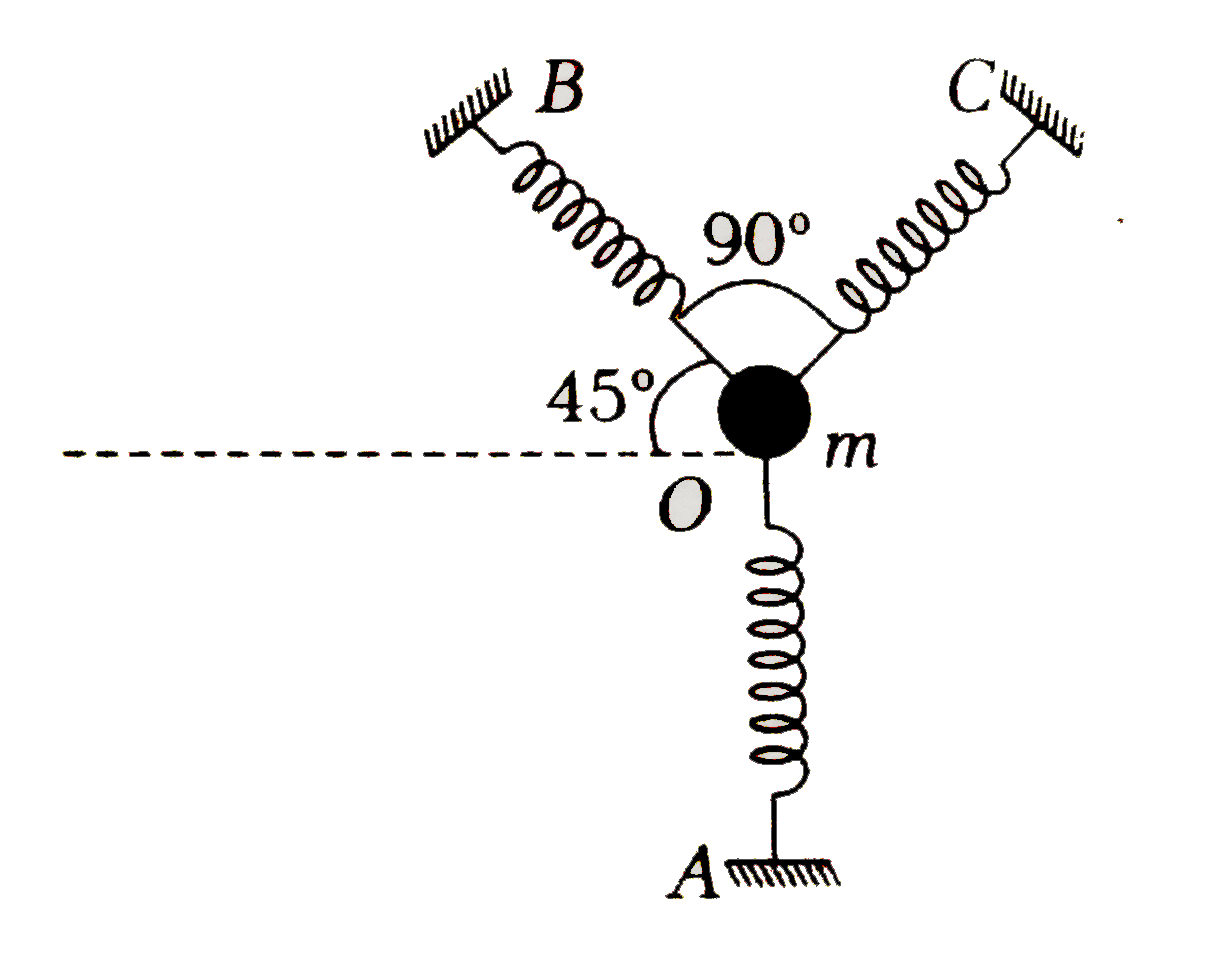

View Solution