In the figure shown the time period and the amplitude respectively, when m is left from rest when spring is relaxed are (the inclined plane is smooth)

2π√mk,mgsinθk
2π√msinθk, 2mgsinθk
2π√mk, mgcosθk
None of these
The correct Answer is:A
In equilibrium, let x0 is extention in spring then
kx0=mgsinθ
∴x0=mgsinθk = amplitude of oscillations.
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBook:DC PANDEYChapter:SIMPLE HARMONIC MOTIONExercise:Level 1 Subjective
Explore 39 Videos
- SIMPLE HARMONIC MOTIONBook:DC PANDEYChapter:SIMPLE HARMONIC MOTIONExercise:Level 2 Single Correct
Explore 28 Videos
- SIMPLE HARMONIC MOTIONBook:DC PANDEYChapter:SIMPLE HARMONIC MOTIONExercise:Level 1 Assertion And Reason
Explore 10 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBook:DC PANDEYChapter:SEMICONDUCTORS AND ELECTRONIC DEVICESExercise:More than One Option is Correct
Explore 3 Videos
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBook:DC PANDEYChapter:SOLVD PAPERS 2017 NEET, AIIMS & JIPMERExercise:Solved paper 2018(JIPMER)
Explore 38 Videos
Similar Questions
A block of mass m connected with a smooth prismatic wedge of mass m is released from rest when the spring is relaxed. Find the angular frequency of oscillation.

View SolutionIn the figure shown , all surface are smooth . Acceleration of mass '4m' , when the system Is released from rest will be

View Solution
Knowledge Check
A mass M is attached to a horizontal spring of force constant k fixed one side to a rigid support as shown in figure. The mass oscillates on a frictionless surface with time period T and amplitude A. When the mass M is in equilibrium position, another mass m is gently placed on it. When will be the new amplitude of ocillation?
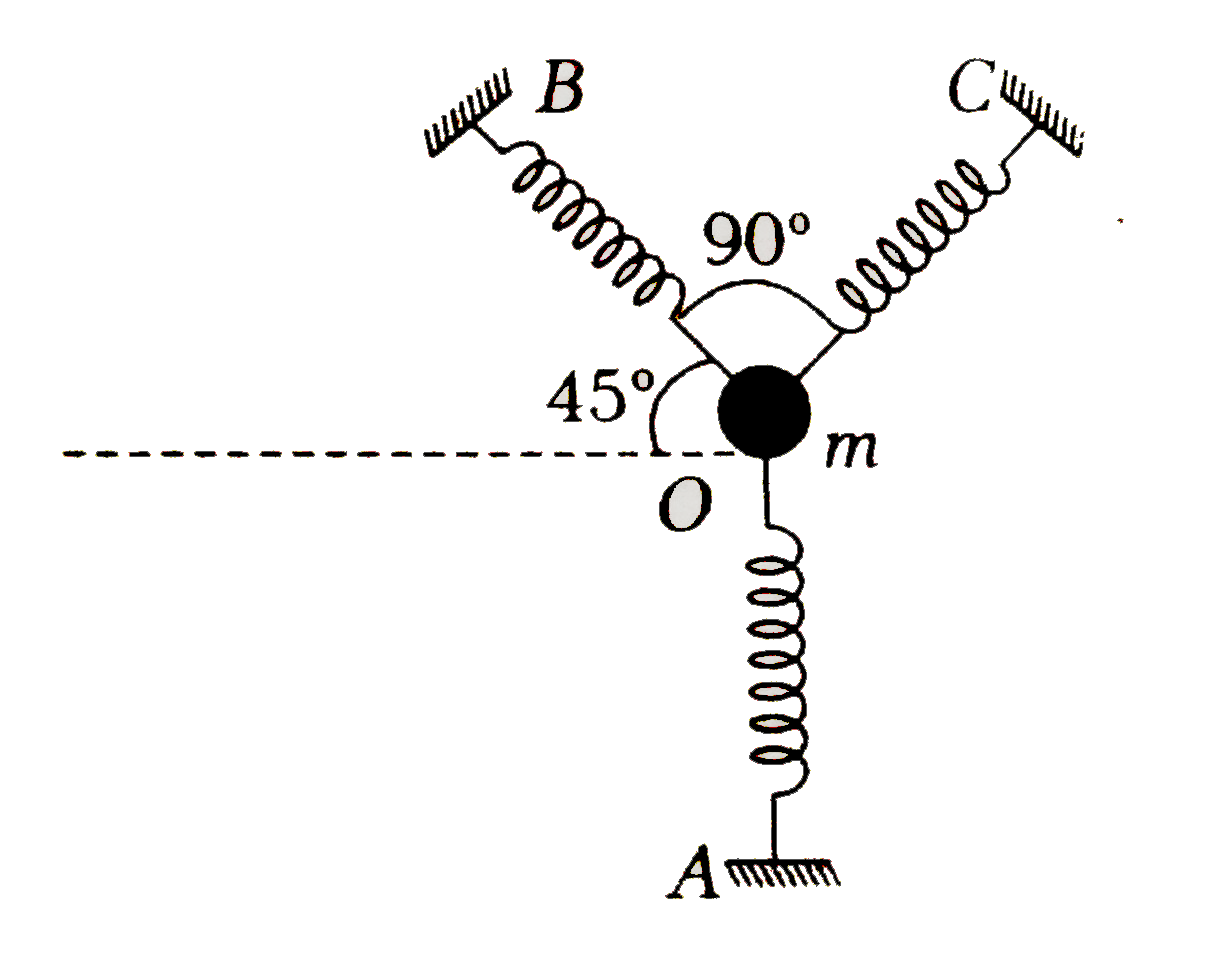
 A√(M+m)MAB√(M−m)MAC√M(M+m)AD√M(M−m)A
A√(M+m)MAB√(M−m)MAC√M(M+m)AD√M(M−m)AThe ratio of the time taken by a solid sphere and that taken by a disc of the same mass and radius to roll down a smooth inclined plane from rest from the same height -
A15:14B√15:√14C14:15D√14:√15In the given figure, a mass M is attached to a horizontal spring which is fixed on one side to a rigid support. The spring constant of the spring is k. The mass oscillates on a frictionless surface with time period T and amplitude A. When the mass is in equilibrium position, as shown in the figure, another mass m is gently fixed upon it. The new amplitude of oscillation will be :
 AA√M−mMBA√MM+mCA√M+mMDA√MM−m
AA√M−mMBA√MM+mCA√M+mMDA√MM−m
Blocks A and B shown in the figure are having equal masses m. The system is released from rest with the spring unstretched. The string between A and ground is cut, when there is maximum extension in the spring. The acceleration of centre of mass of the two blocks at this instant is
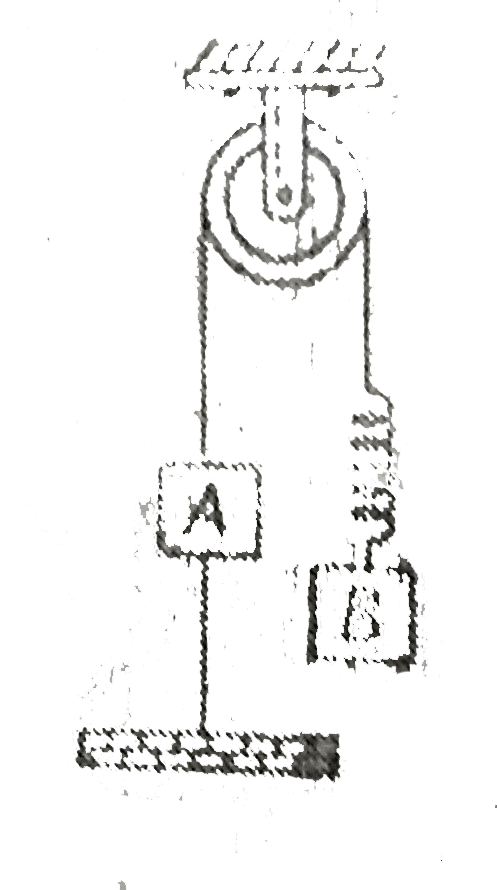
View SolutionOne end of a spring is fixed to the ceiling and other end is attached to a block. The block is released when spring is relaxed. The product of time period and amplitude is 8 S.I. units. If spring is cat in two equal parts and the two springs are attached to the block as shown in figure. The block is released when both springs are relaxed. Now find the product of time period and amplitude in S.I. units.
'(##CEN_KSR_PHY_JEE_C16_E01_028_Q12##)'
View SolutionFind the time period of mass M when displaced from its equilibrium position and then released for the system shown in figure.

View SolutionA smooth wedge of mass m and angle of inclination 60∘ rests unattached between two springs of spring constant K and 4k on a smooth horizontal plane both springs in the unextended position the time period of small oscillation of the wedge (assuming that the springs are constrained to get compressed along their length) equals
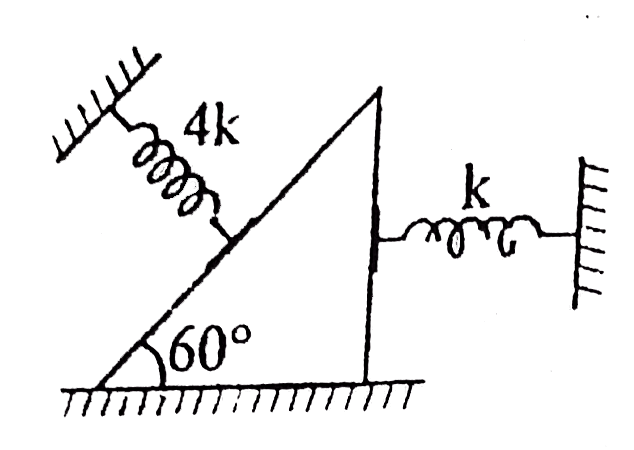
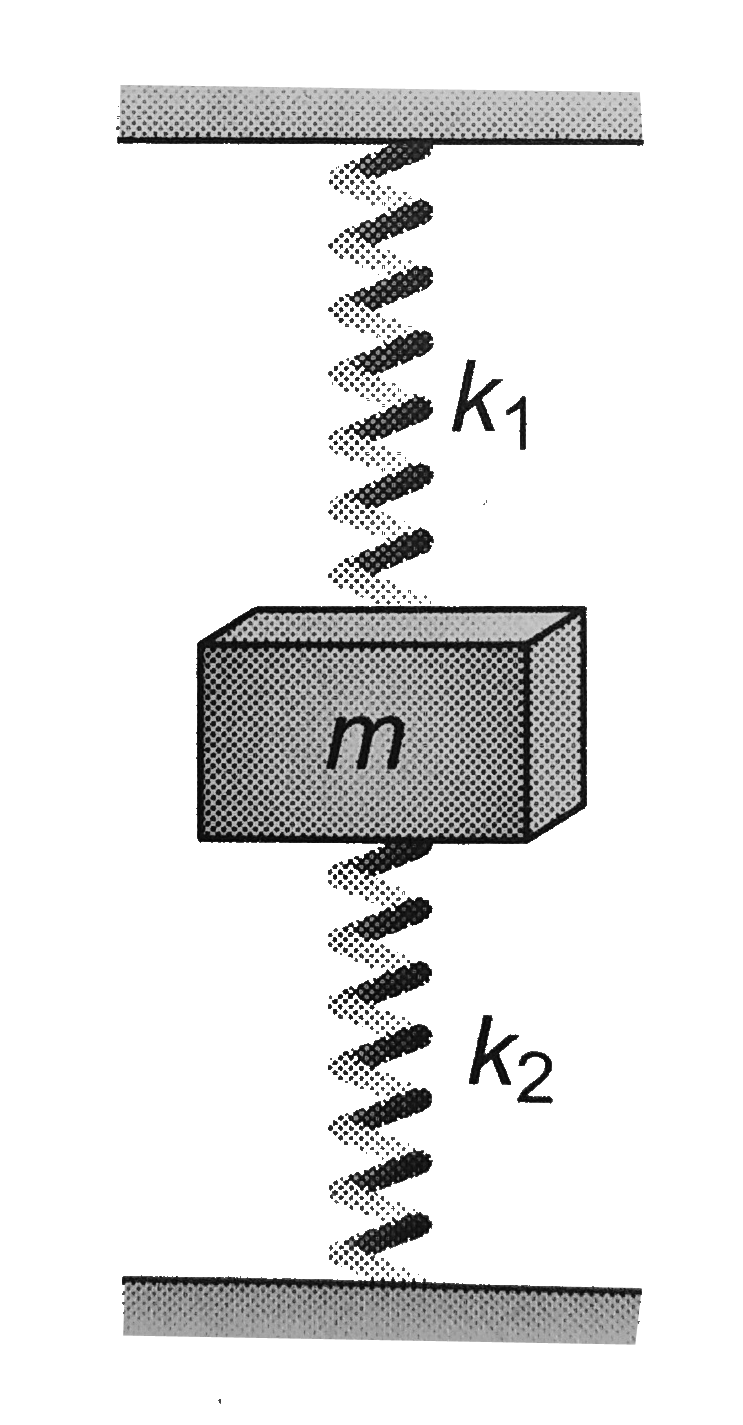
View SolutionIn the figure shown a block of masss m is atteched at ends of two spring The other ends of the spring are fixed The mass m is released in the vertical plane when the spring are released The velocity of the block is maximum when
View Solution

