In the figure shown, the instantaneous speed of end A of the rod is v to the left. The angular velocity of the rod of length L must be


component of velocities of A and B along AB should be same
∴vAcos30∘=vBcos30∘
∴vB=vA=v
ω=relative velocity ⊥toABAB
=vAsin30∘+vBsin30∘l
=vl (as vA=vB=v)
Topper's Solved these Questions
- ROTATIONAL MECHANICSBook:DC PANDEYChapter:ROTATIONAL MECHANICSExercise:Exercise 12.3
Explore 4 Videos
- ROTATIONAL MECHANICSBook:DC PANDEYChapter:ROTATIONAL MECHANICSExercise:Exercise 12.4
Explore 11 Videos
- ROTATIONAL MECHANICSBook:DC PANDEYChapter:ROTATIONAL MECHANICSExercise:Exercise 12.1
Explore 10 Videos
- ROTATIONBook:DC PANDEYChapter:ROTATIONExercise:(C) Chapter Exercises
Explore 39 Videos
- ROTATIONAL MOTIONBook:DC PANDEYChapter:ROTATIONAL MOTIONExercise:Integer Type Questions
Explore 17 Videos
Similar Questions
A rod od length l is moving in a vertical plane (x−y) when the owest point A of the rod is moved with a velociy v. find the a angular velocity of the rod and b velocity of the end B.

View SolutionA uniform rod of mass m and length l is on the smooth horizontal surface. When a constant force F is applied at one end of the rod for a small time t as shown in the figure. Find the angular velocity of the rod about its centre of mass.
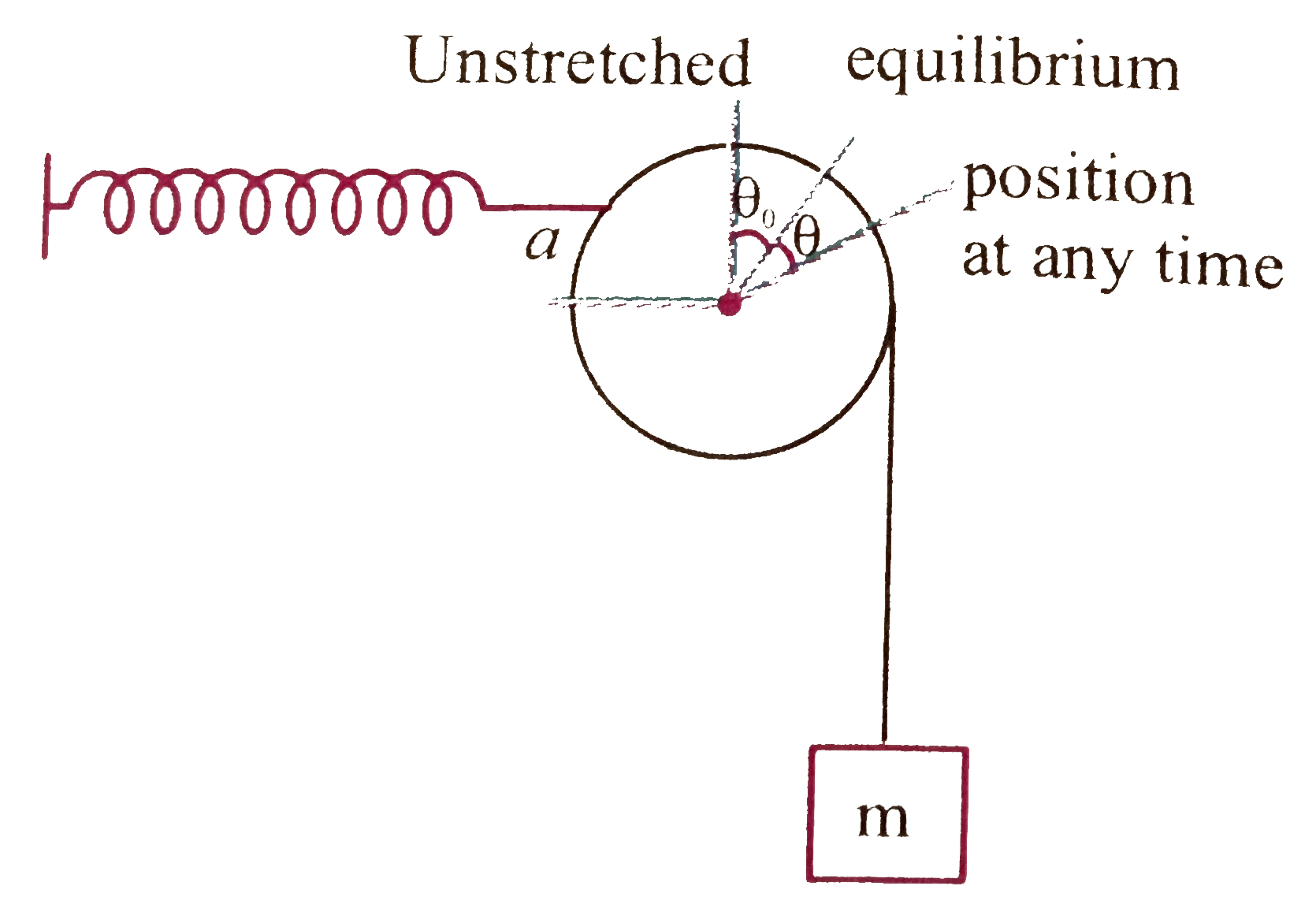
View Solution
Knowledge Check
In the figure shown the instantaneous speed of end A of the rod is v to the left the angular velocity of the rod of lengthL must be
 Av/2LBv/LCv√3/2LDnone
Av/2LBv/LCv√3/2LDnoneIn the figure shown a smooth ring is connected to rod AB, while rod CD passes through ring. At the given instant angular velocity of rod AB about hinge A is 1 rod/s and AC=CB. Instantaneous angular velocity of rod CD about hinge C is
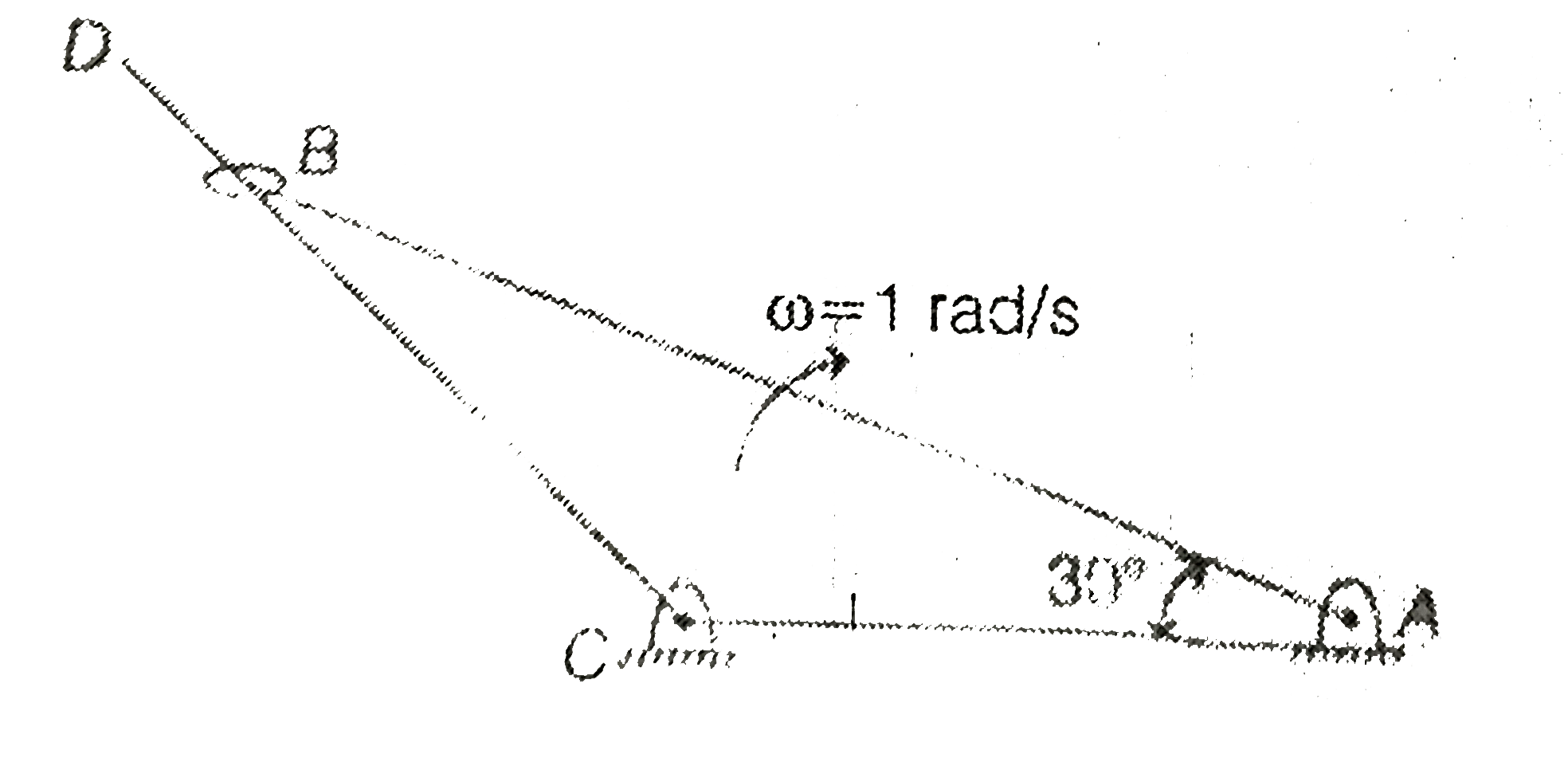 A1rad/sB1/2rad/sC√3/2rad/sD3/2rad/s
A1rad/sB1/2rad/sC√3/2rad/sD3/2rad/sConsider a rod of mass M and length L pivoted at its centre is free to rotate in a vertical position plane. The rod is at rest in the vertical position. A bullet of mass M moving horizontally at a speed v strikes and embedded in one end of the rod. The angular velocity of the rod just after the collision will be.
Av/LB2v/LC3v/2LD6v/L
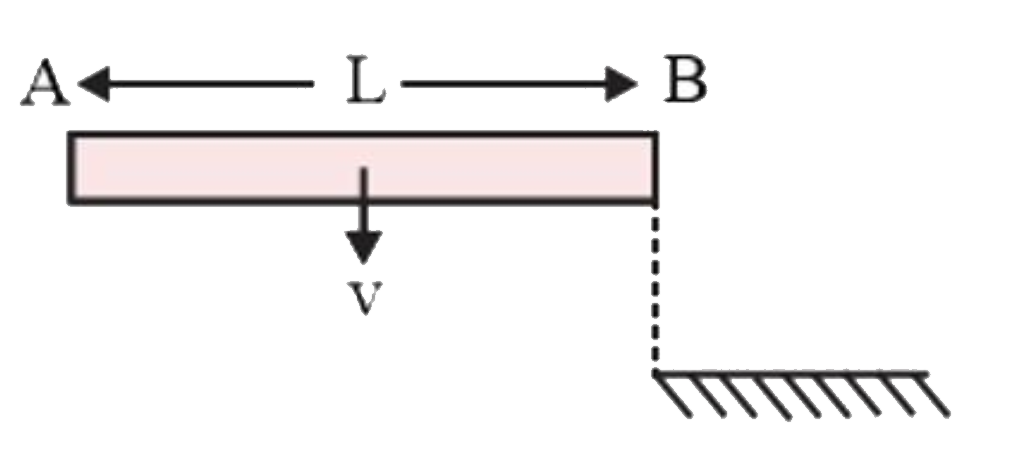
A rod AB of length L and mass M is free to move on a frictionless horizontal surface . It is moving with a velocity v , as shown in figure. End B of rod AB strikes the end of the wall. Assuming elastic impact , the angular velocity of the rod AB , just after
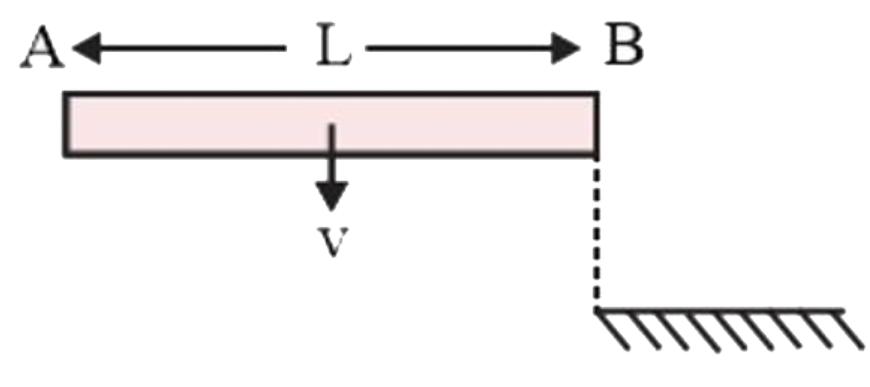
View SolutionA rod AB of mass M and length 8l lies on a smooth horizontal surface. A particle, of A mass m and velocity v0 strike's the rod perpendicular to its length, as shown in Fig. As a result of the collision, the centre of mass of the rod attains a speed of v0/8 and the particle rebounds back with a (not to scale) speed of v0/4. Find the following: a. The ratio M/m. b. The angular velocity of the rod about O. c. The coefficient of restitution 'e' for the collision. d. The velocities of the ends 'A' and 'B' of the rod, namely, vA and vB respectively.
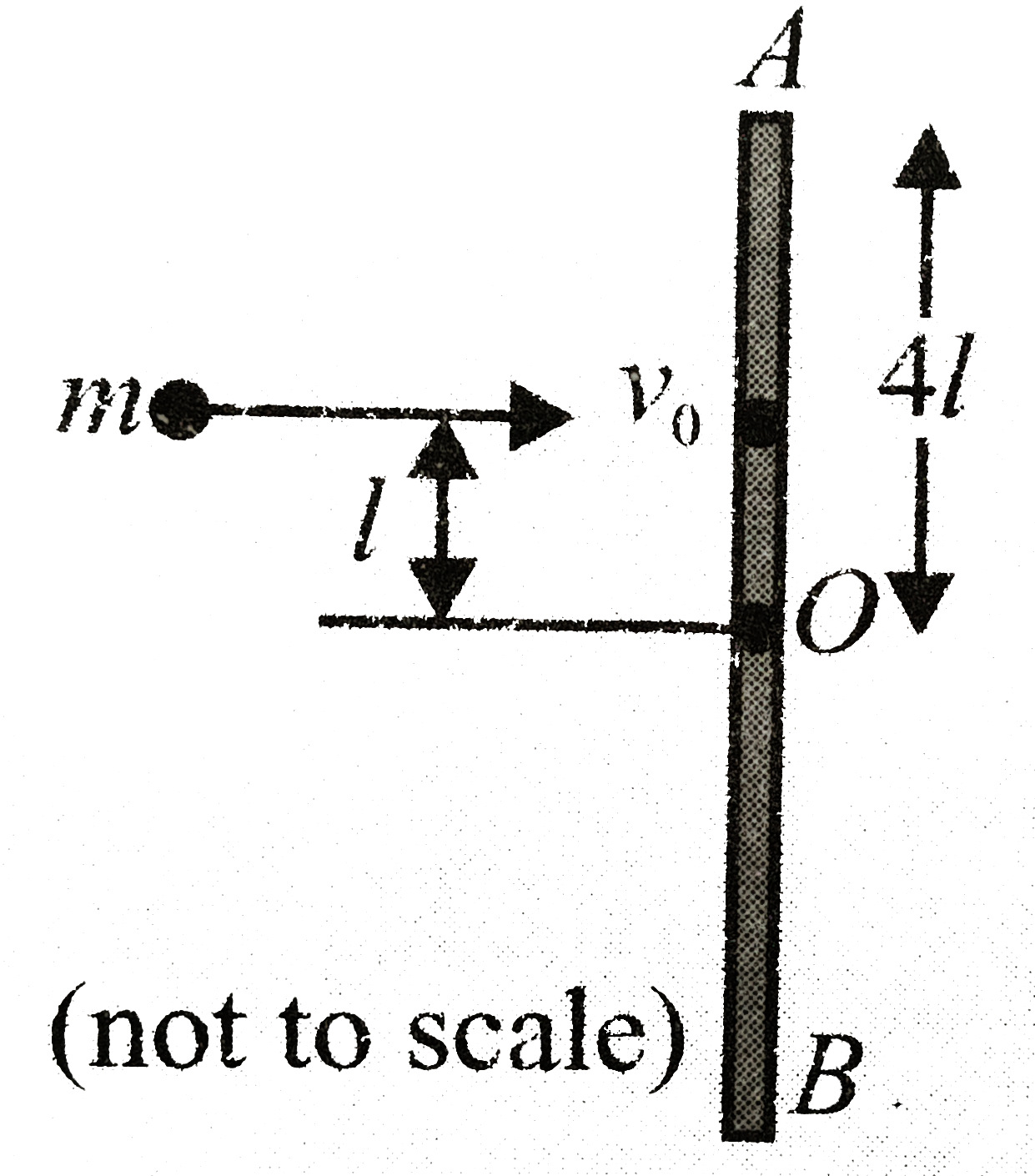
View Solution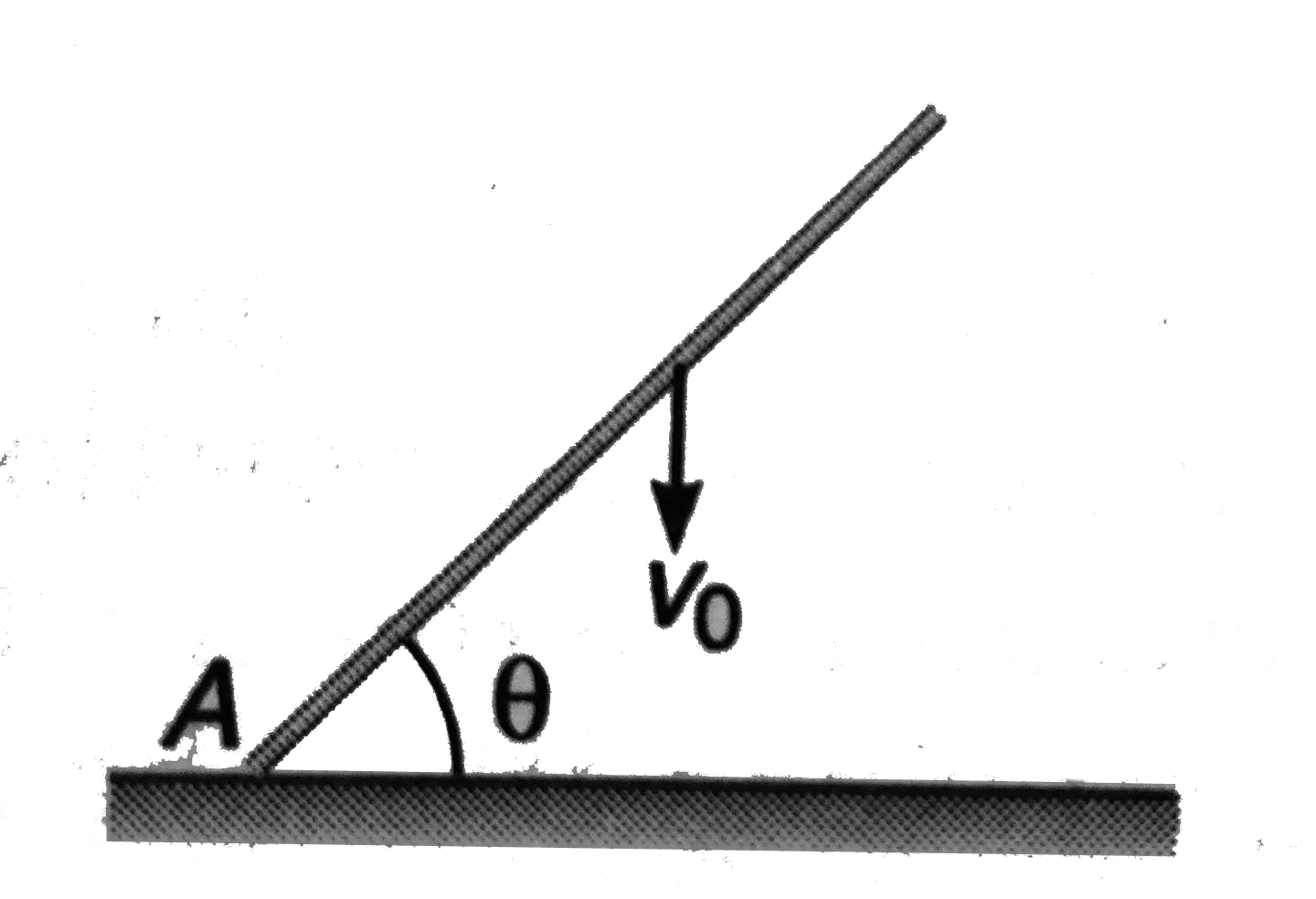
A rod of length l forming an angle θ with the horizontal strikes a frictionless floor at A with its centre of mass velocity v0 and no angular velocity. Assuming that the impact at A is perfectly elastic. Find the angular velocity of the rod immediately after the impact.
View SolutionA uniform rod of length L and weight W is suspended horizontally by two vertical ropes as shown. The first rope is attached to the left end of the rod while the second is attached to the left end of the rod while the second rope is attached a distance L/4 from the right end. The tension in the second rope is.
 .
.
View SolutionA rod AB of length L and mass M is free to move on a frictionless horizontal surface. It is moving with a velocity v, as shown in figure. End B of rod AB strikes the end of the wall. Assuming elastic impact, the angular velocity of the rod AB, just after impact, is
View Solution

