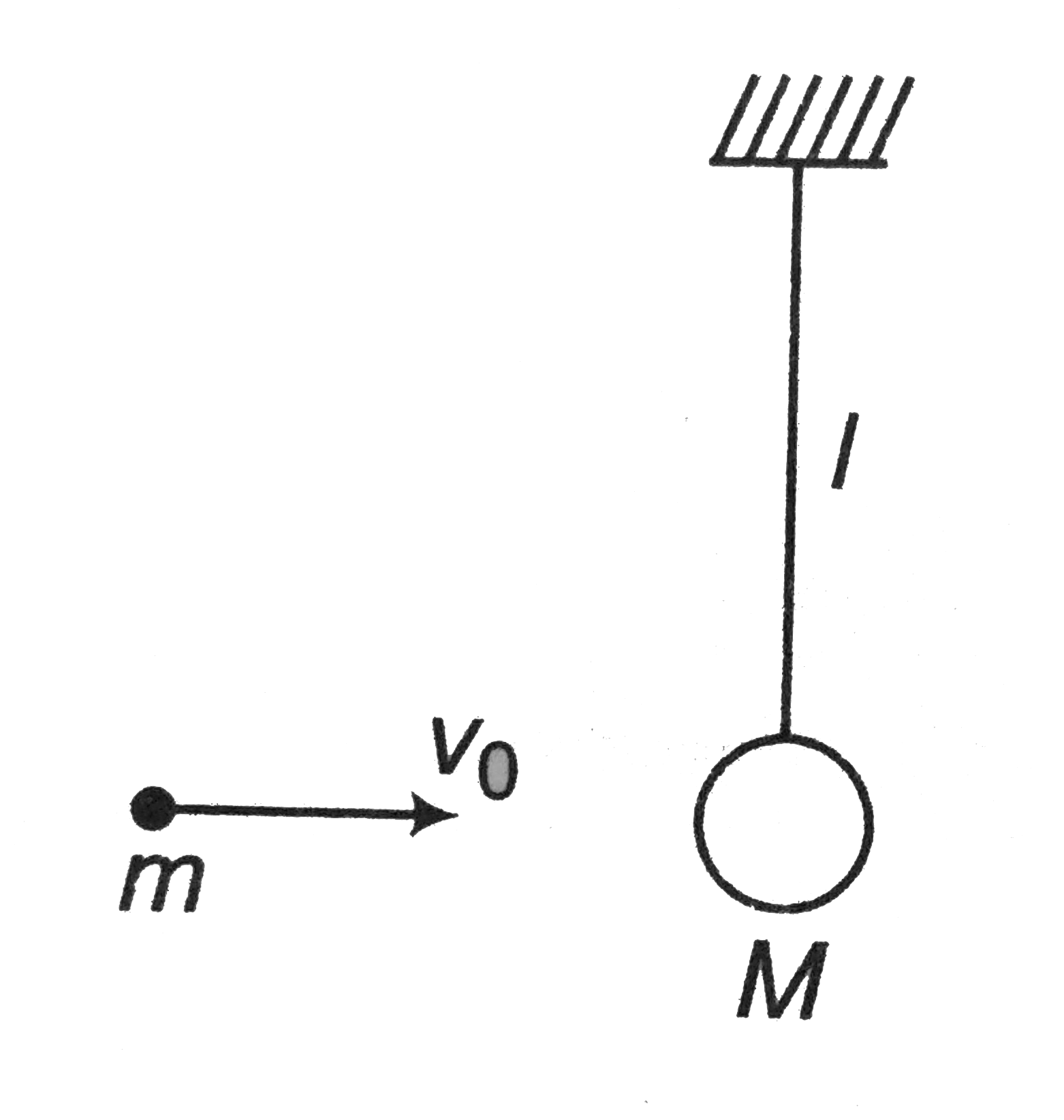
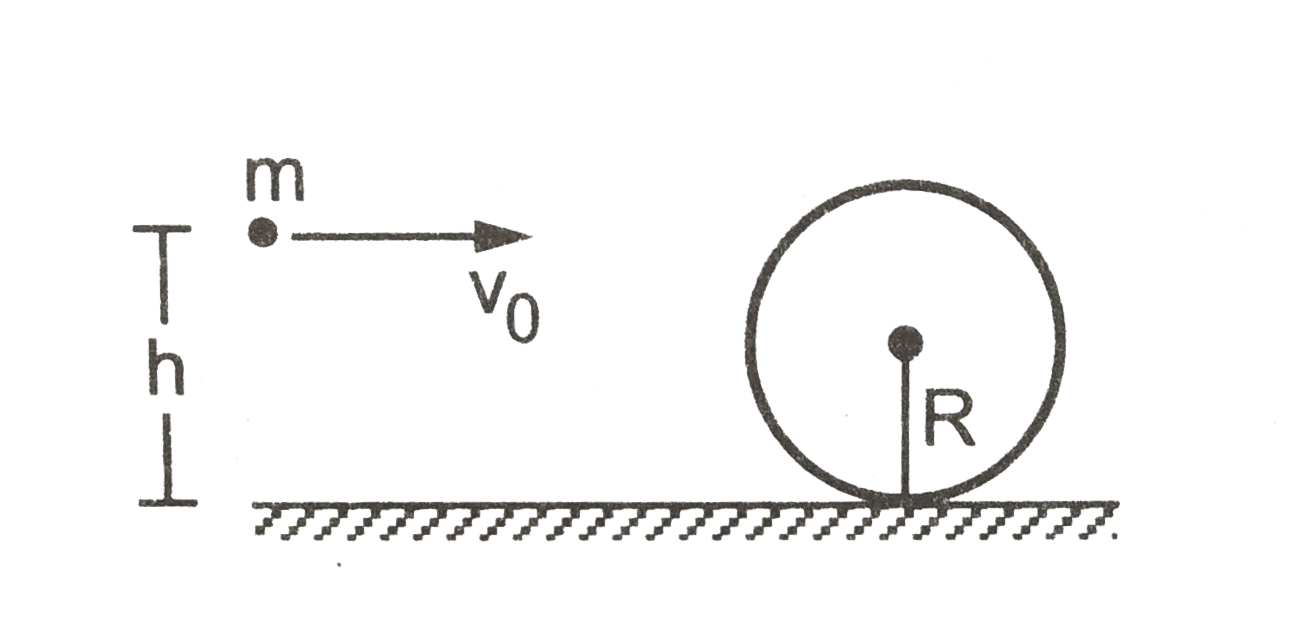
In the situation discussed above, find
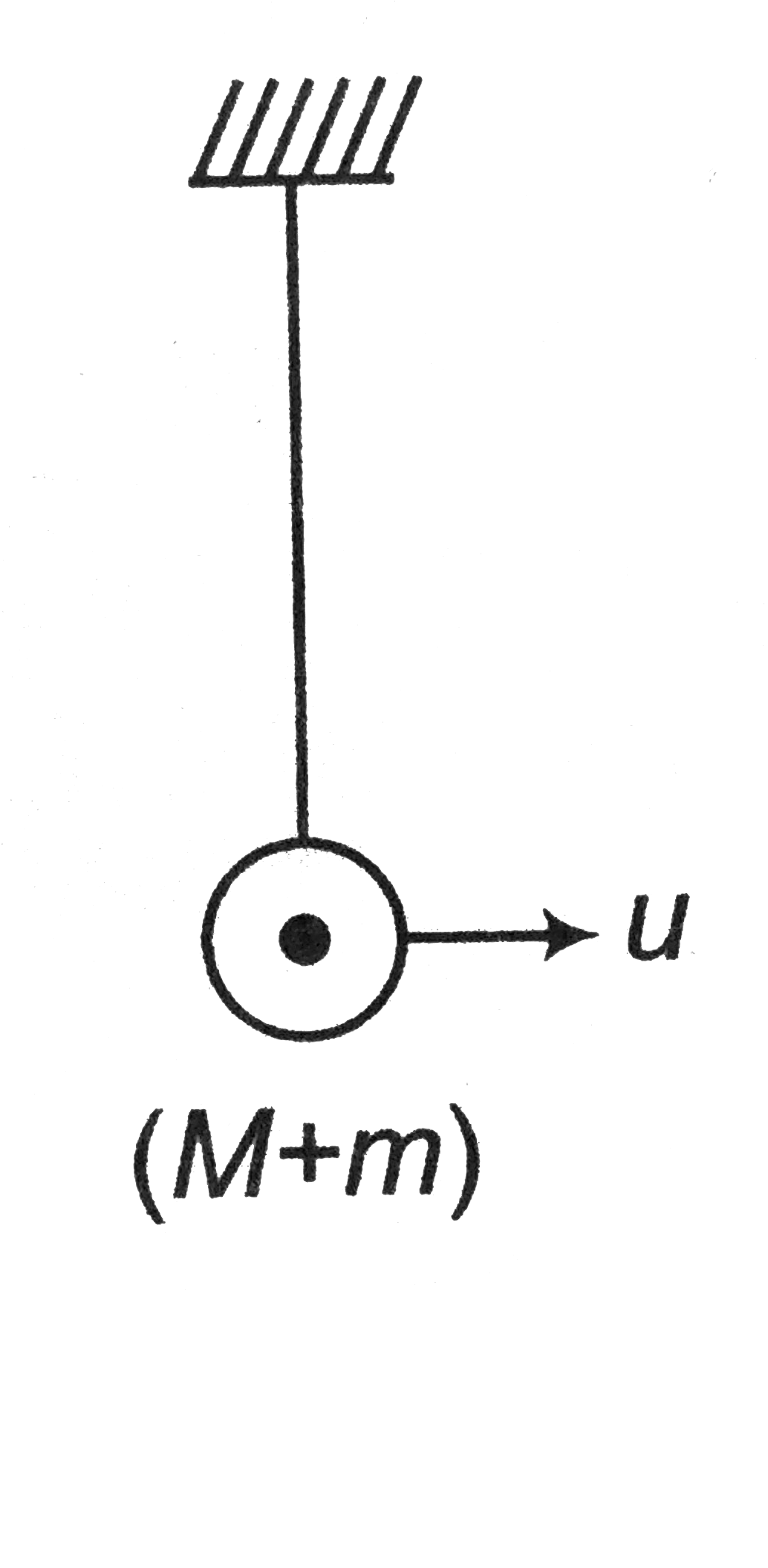
(a) velocity of combined mass just after collision at the bottommost point (oru).
(b) loss of mechanical energy during collision.
(c) minimum value of v0 so that the combined mass completes the vertical circular motion.
The correct Answer is:A, B
(a) Appying conservation of linear momentum, just before and just after collision.
pi=pf⇒mv0=(M+m)u⇒u=mv0M+m
(b) Loss of mechanical energy during collision,
=Ei−Ef (E=mechanical energy)
=12mv0−12(M+m)u2
=12mv20−12(M+m)[mv0M+m]2
=12Mmv20(M+m)
(c) For completing the vertical circular motion, velocity at bottommost point, u≥√5gl
∴mv0M+m≥√5gl⇒∴v0≥M+mm√5gl
or (v0)min=M+mm√5gl
Topper's Solved these Questions
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBook:DC PANDEYChapter:CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONExercise:Type 1
Explore 1 Video
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBook:DC PANDEYChapter:CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONExercise:MiscellaneousExamples
Explore 9 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBook:DC PANDEYChapter:CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONExercise:Level 2 Subjective
Explore 21 Videos
- CENTRE OF MASS, IMPULSE AND MOMENTUMBook:DC PANDEYChapter:CENTRE OF MASS, IMPULSE AND MOMENTUMExercise:Comprehension type questions
Explore 15 Videos
- CIRCULAR MOTIONBook:DC PANDEYChapter:CIRCULAR MOTIONExercise:Medical entrances s gallery
Explore 19 Videos
Similar Questions
In the figure shown in the text, if the block is a cube of side a
find
(a). ω just after impact
(b). Loss of mechanical enegy during impact
(c) minimum value of v so as the block overcomes the obstacle and does not turn back.
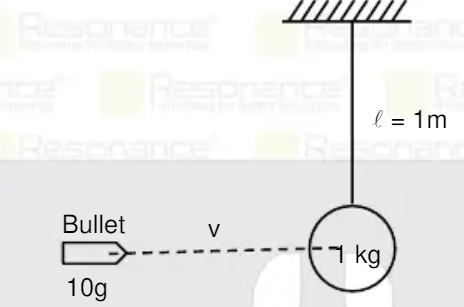
View SolutionA bullet of mass 10g travelling with velocity v collides with pendulum mass system of mass 1kg and length 1m and embedded in it as shown. Find minimum value of v so that pendulum mass undergoes complete circular motion.
View Solution
Knowledge Check
A bullet of mass 20g moving horizontally strikes a block of mass 480g suspended by a string of length 2m. If the collision is completely inelastic , the minimum velocity of bullet , so that the combined mass complete vertical circle should be
A100m/sB150m/sC200m/sD250m/sA point mass m is connected with ideal inextensible string of length l and other end of string is tied at point O as shown in the figure. The string is made horizontal and mass is released from point A to perform vertical circular motion. There is a nail at point N such that ON =r . Find the value of r so that mass m is able to just perform complete vertical circular motion about point N.
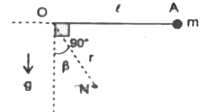 Al2+2cosβB3l3+2cosβCl3+2sinβD3l2+2sinβ
Al2+2cosβB3l3+2cosβCl3+2sinβD3l2+2sinβ
The sphere shown in figue lies on a rough plane when a particle of mass m travbelling at a speed v0 collides and sticks with it. If the line of motion of the particle is at a distance h above the plane, find a. the linear speed o the combine dsystem just after teh collision b. the angular speed of the system about the centre of the sphere just the collistion c. the value of h for which the sphere starts pure rolling on the plane Assume that the mass M of the sphesre is large compared to teh mass of the partcle so that is large compared toteh mass of the particle so that teh centre of mass of the combined system is not appreciably shifted from the centre of the sphere.
View SolutionA wooden log of mass M and length L is hinged by a frictionless nail at O. A bullet of mass m strikes with velocity v and sticks to it. Find the angular velocity of the system, immediately after the collision about O. Also, calculate the minimum value of v so that log becomes horizontal after collision.
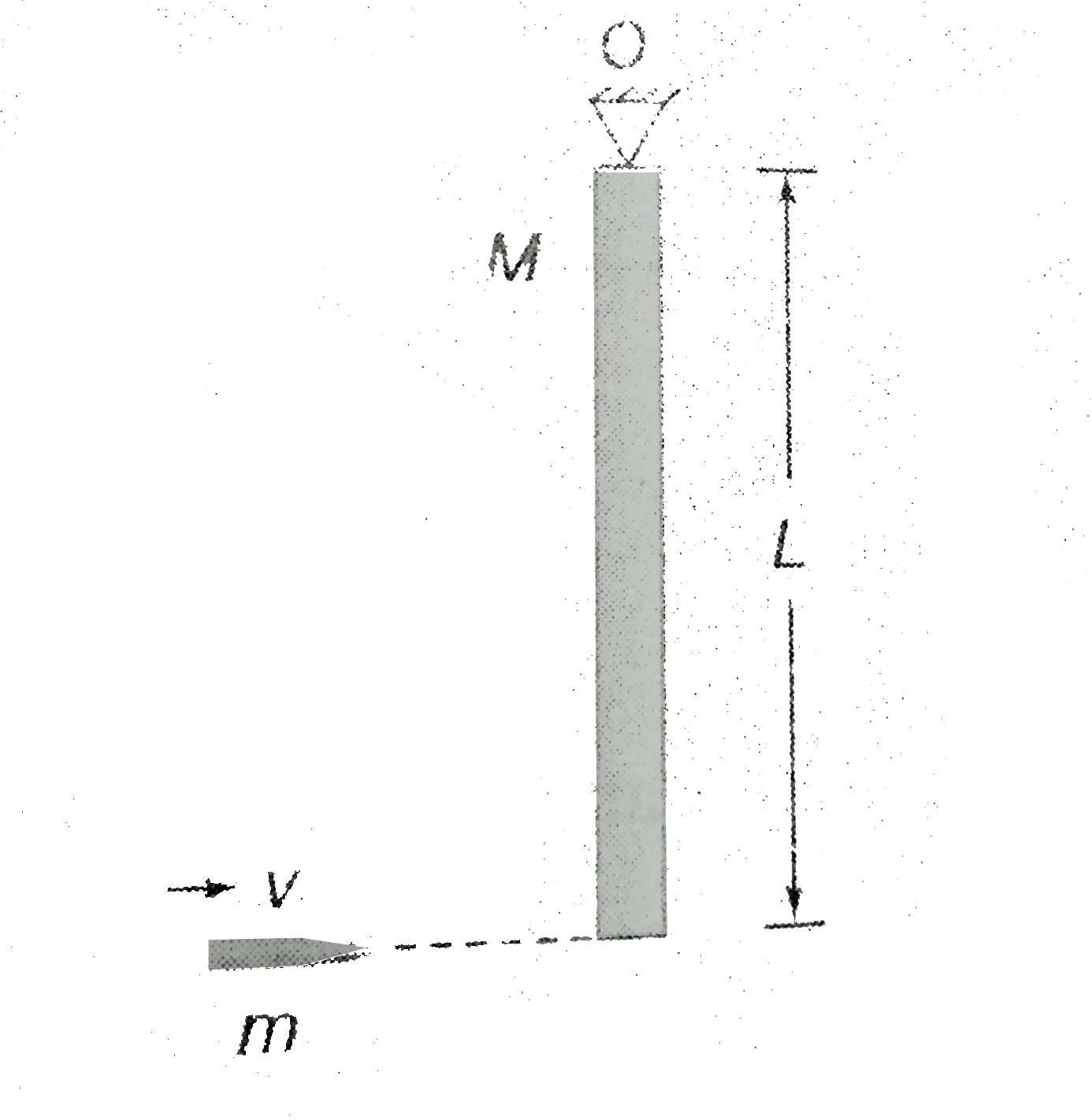
View SolutionTwo blocks A and B of mass m and 2m respectively are moving towards a massive (mass>>2m) cliff with velocities 2v and v respectively. The cliff moves with a velocity v. If the coefficient of restitution of collision at the surface of the cliff is e=1/2, find the:

a. velocity of the block B just after colliding with the cliff.
b. work done by the cliff during collision.
c. maximum compression of the spring of stiffness k which is fitted with the block B.
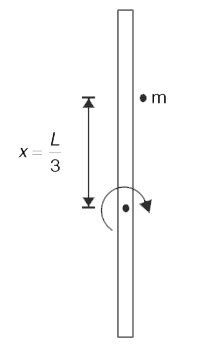
View SolutionA uniform thin stick of mass M=24kg and length L rotates on a friction less horizontal plane, with its centre of mass stationary. A particle of mass m is placed on the plane at a distance x=L3 from the centre of the stick . This stick hits the particle elastically
(a) Find the value of m so that after the collision, there is no rotational motion of the stick
(b) For what minimum of x can we get a value of ‘m’ so that the rod has no rotational motion after elastic collision ?
View SolutionSuppose the particle of the previous problem has a mass m and a speed v before the collision and it sticks to the rod after the collision. The rod has a mass M. a. Find the velocity of the particle with respect to C of the system consituting the rod plus the particle. b. Find the velociyt of the particle with respect to C before the collision. c. Find the velocity of the rod with respect to C before the colision. e. find the moment of inertia of the system about the vertical axis through the centre of mass C after the collision. f. Find the velociyt of the centre of mass C and the angular velocity of the system about the centre of mass after the collision.
View SolutionTwo balls A and B. are of the sme size but the mass of A is double that of B. they move along the sme line in opposite direction. A with velocity 2μ and B with velocity 3μ If their total kinetoc energy after collision is half their total kinetic energy before collision find the coefficient of restitution. Find also their velocities after collision.
View Solution

