Two balls of masses m and 2m and momenta 4p and 2p (in the directions shown) collide as shown in figure. During collsion, the value of linear impulse between them is J. In terms of J and p find coefficient of restitution 'e'. Under what condition collision is elastic. Also find the condition of perfectly inelastic collision.

The correct Answer is:A, B, C
Directions of linear impulses on the two colliding bodies at the time of collision are shown in fig.

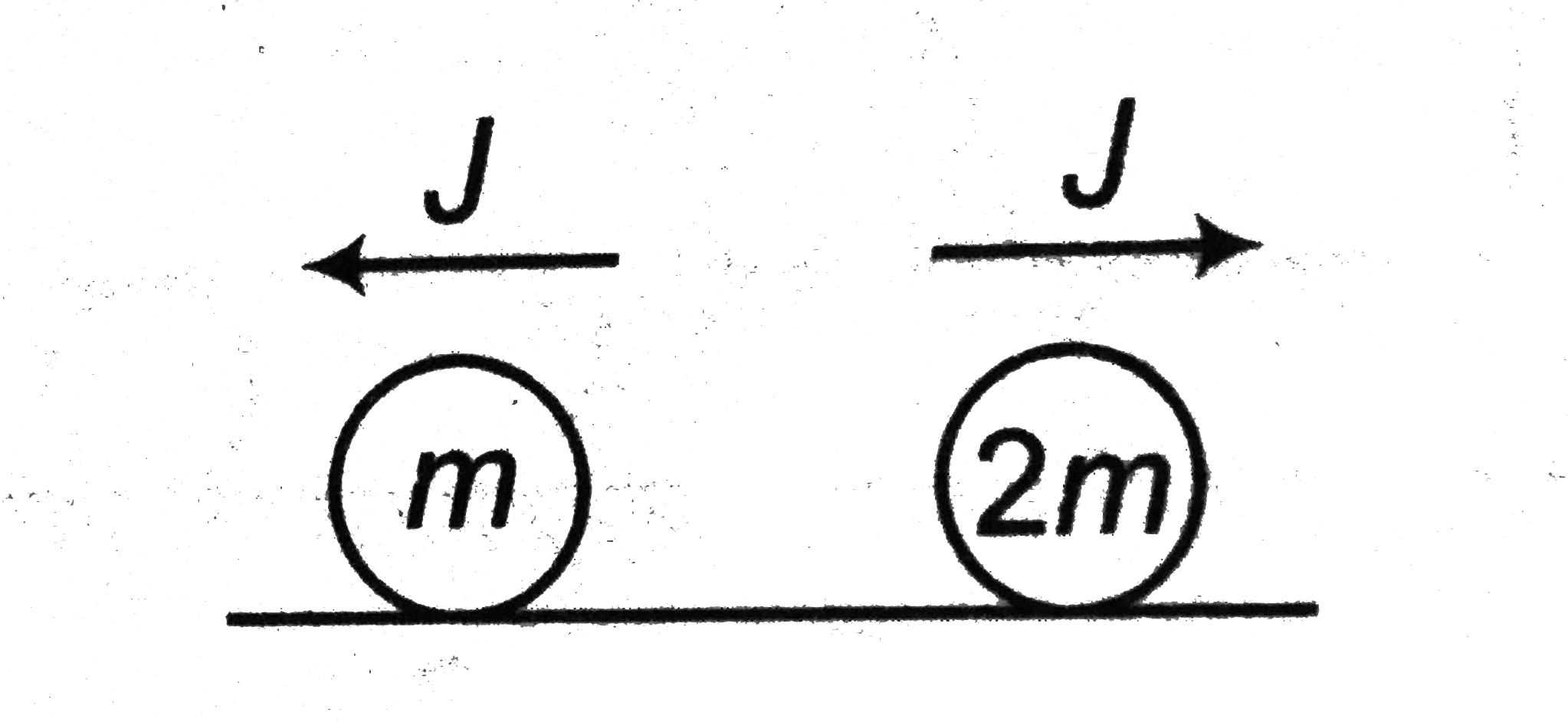
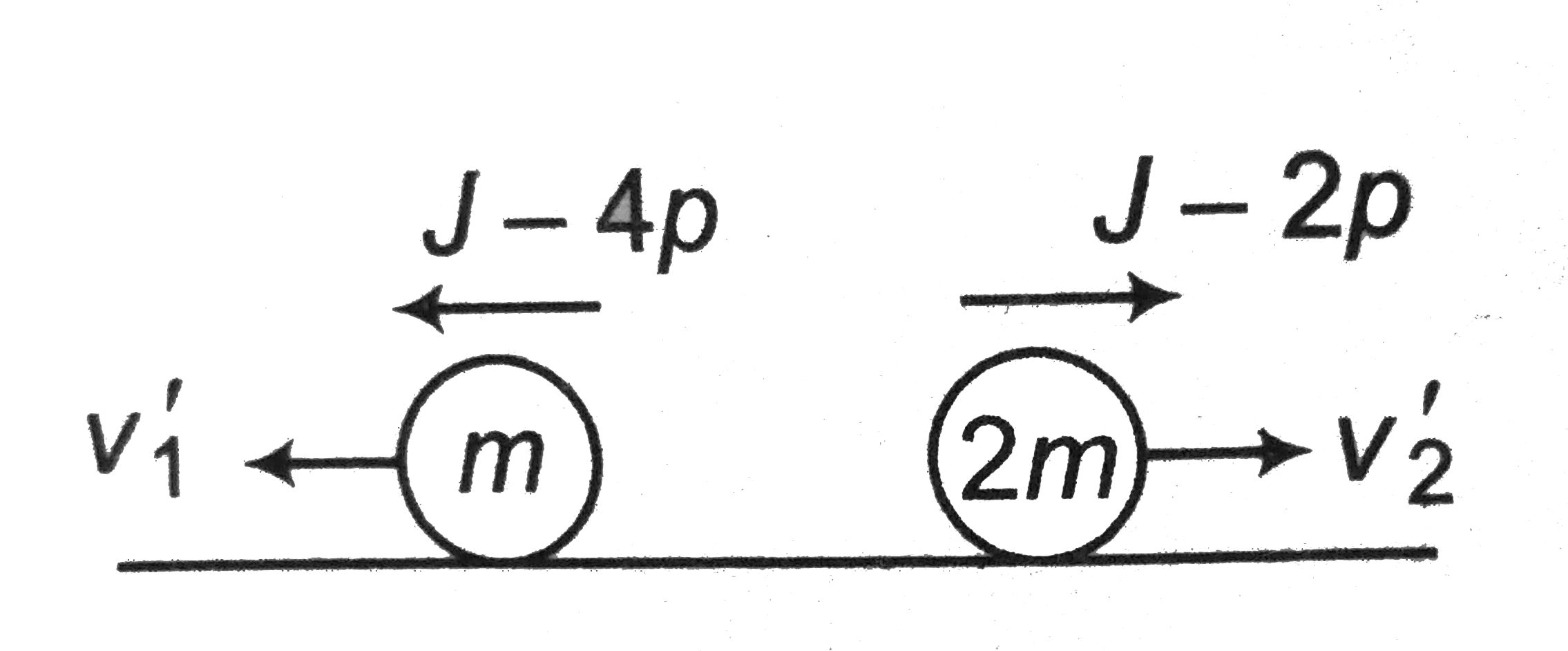
Linear impulse is equal to the change in linear momentum. Hence, momenta of the balls after collision are shown in figure.
Let v1 and v2 are their velocities before collision [in the directions shown in figure(a)] and v′1 and v2 are the velocities after collision as shown in figure (c).
v=("linear momentum"/("mass")
e=("relative speed of separation")/("relative speed of approach")<br>ore=(v_1'+v_2')/(v_1+v_2)=((J-4p)/(m)+(J-2p)/(2m))/((4p)/(m)+(2p)/(2m))<br>ore=(3J-10p)/(10p)=(3J)/(10p)-1<br>Forel∗iccollision,<br>e=1rArr(3J)/(10p)=2orJ=(20)/(3p)<br>Forperfectly∈el∗iccollision,<br>e=0rArr(3J)/(10p)=1orJ=10/3p
Topper's Solved these Questions
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBook:DC PANDEYChapter:CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONExercise:Type 1
Explore 1 Video
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBook:DC PANDEYChapter:CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONExercise:MiscellaneousExamples
Explore 9 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBook:DC PANDEYChapter:CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONExercise:Level 2 Subjective
Explore 21 Videos
- CENTRE OF MASS, IMPULSE AND MOMENTUMBook:DC PANDEYChapter:CENTRE OF MASS, IMPULSE AND MOMENTUMExercise:Comprehension type questions
Explore 15 Videos
- CIRCULAR MOTIONBook:DC PANDEYChapter:CIRCULAR MOTIONExercise:Medical entrances s gallery
Explore 19 Videos
Similar Questions
Two toy trains each of mass 'M' are moving in opposite directions with velocities v1 and v2 over two smooth rails. Two stuntmen of mass 'm' each are also moving with the trains (at rest w.r.t. trains). When trains are opposite to each other the stuntmen interchange their positions, then find the final velocities of the trains.
View SolutionThe friction coefficient between the horizontal surface and each of the block shown in the figure is 0.2. The collision between the blocks is perfectly elastic. Find the separation between them when they come to rest. (Take g=10m/s2).

View SolutionA ladder AP of length 5m inclined to a vertical wall is slipping over a horizontal surface with velocity of 2m/s, when A is at distance 3m from ground. What is the velocity of COM at this moment?

View SolutionComprehension # 1
If net force on a system in a particular direction is zero (say in horizontal direction), we can apply: ΣmRxR=ΣmLxL,ΣmRvR=ΣmLvL and ΣmRaR=ΣmLaL
Here R stands for the masses which are moving towards right and L for the masses towards left, x is displacement, v is velocity and a the acceleration (all with respect to ground).
A small block of mass m=1kg is placed over a wedge of mass M=4kg as shown in figure. Mass m is released from rest. All surface are smooth. Origin O is as shown.

Final velocity of the wedge is ..........m/s :-
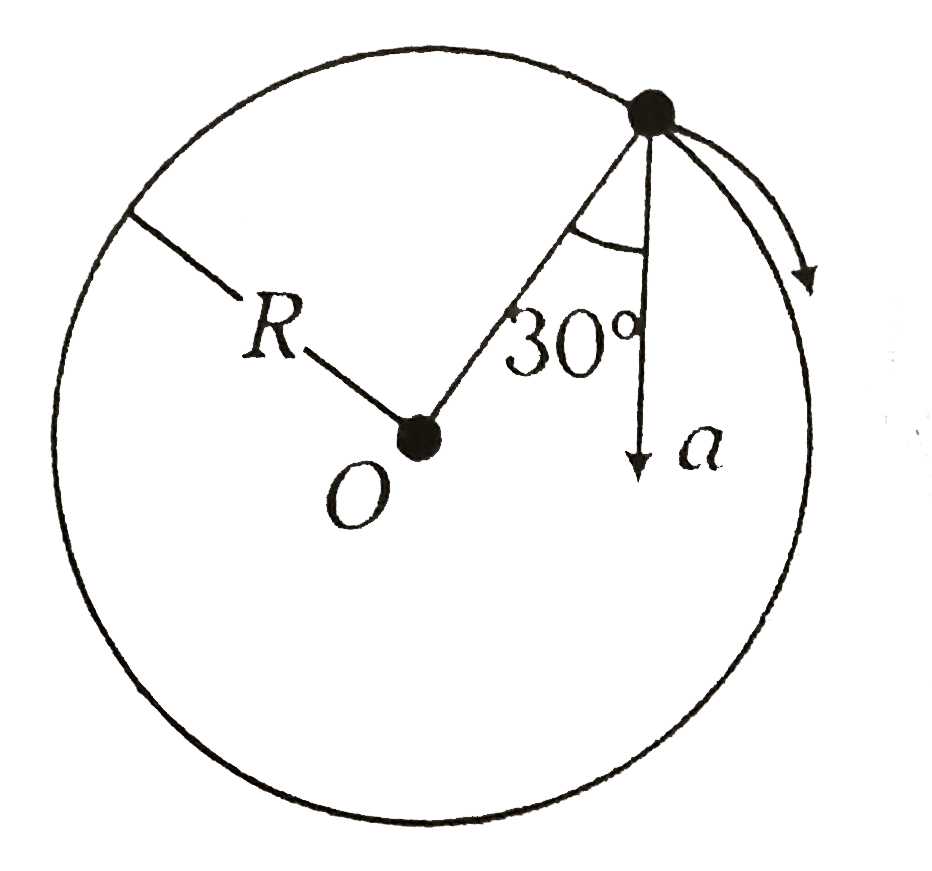
View SolutionIn the given figure, a=15m/s2 represents the total acceleration of a particle moving in the clockwise dirction in a circle of radius R=2.5m at a given instant of time. The speed of the particle is
View SolutionFor a perfectly elastic collision and a perfectly inelastic collision, values of coefficient of restitution are respectively
View SolutionThe coefficient of restitution (e) for a perfectly elastic collision is
View SolutionComprehension # 2 When two bodies collide normally they exert equal and opposite impulses on each other. Impulse = change in linear momentum. Coefficient of restitution between two bodies is given by :- e = |"Relative velocity of separation"|/|"Relative velocity of approach"| = 1 , for elastic collision Two bodies collide as shown in figure. During collision they exert impulse of magnitude J on each other. If the collision is elastic, the value of J is ............. N-s :-
View SolutionComprehension # 2
When two bodies collide normally they exert equal and opposite impulses on each other. Impulse = change in linear momentum. Coefficient of restitution between two bodies is given by :-
e=|Relative velocity of separation||Relative velocity of approach|=1, for elastic collision

Two bodies collide as shown in figure. During collision they exert impulse of magnitude J on each other.
For what value of J (in N−s ) the 2kg block will change its direction of velocity :-
View SolutionThe coefficient of restitution e for a perfectly elastic collision is
View SolutionThe coefficient of restitution e for a perfectly elastic collision is
View SolutionWhat is the value of coefficient of restitution for a perfectly elastic collision?
View SolutionWhat is the value of coefficient of restitution for a perfectly inelastic collision?
View SolutionFor perfectly inelastic collision, coefficient of restitution is
View SolutionWhat is coefficient of restitution for a perfectly inelastic collision ?
View Solution

