A ball of mass m hits a floor with a speed v0 making an angle of incidence α with the normal. The coefficient of restitution is e. Find the speed of the reflected ball and the angle of reflection of the ball.
The correct Answer is:A, B
The component of velocity v0 along common tangent direction v0sinα will remain unchanged. Let v be the component along common normal direction after collision. Applying

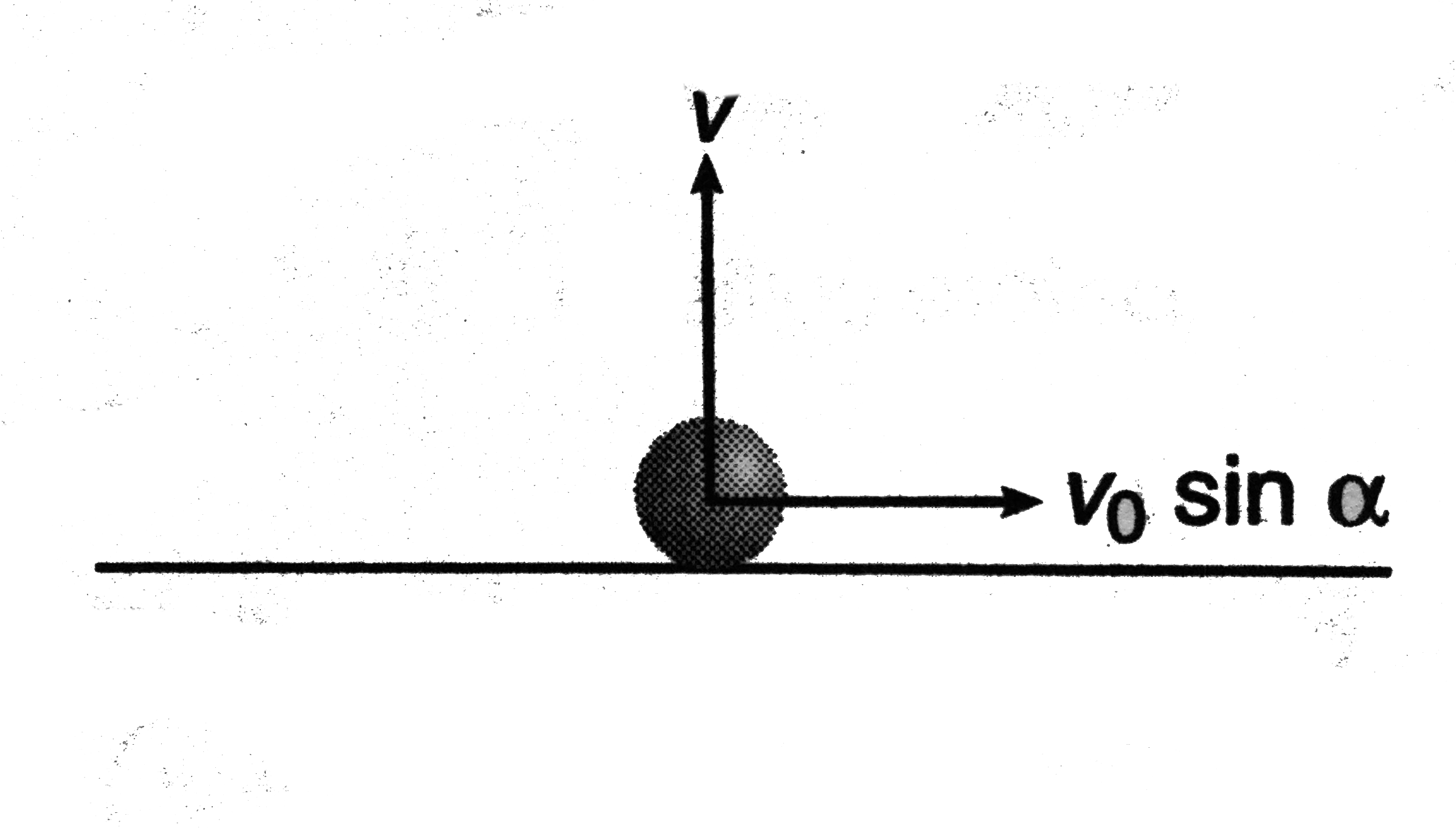
Relative speed of separation =e(relative speed of approach)
along common normal direction, we get
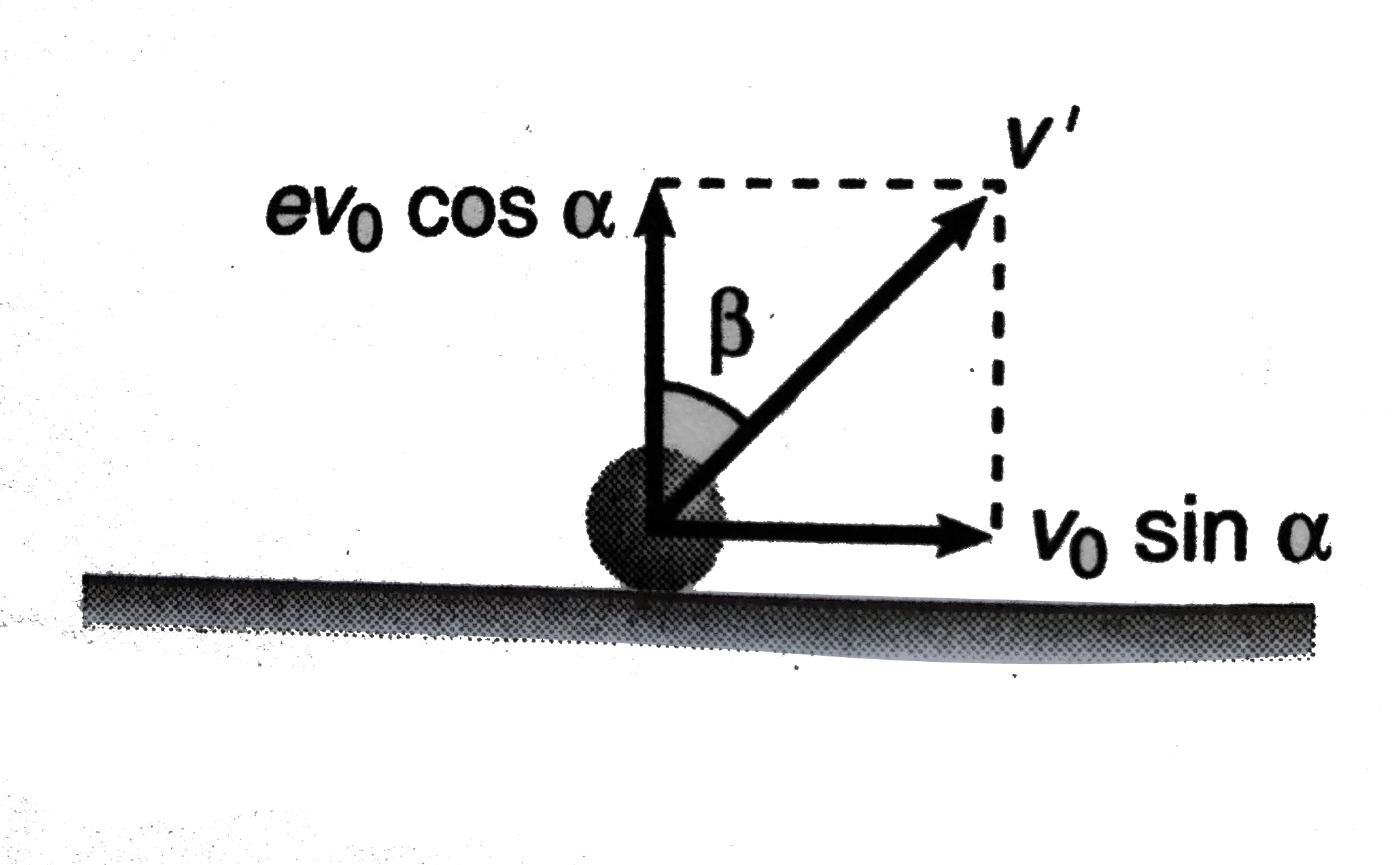
v=ev0cosα
Thus, after collision components of velocity v′ are v0sinα and ev0cosα
∴v′=√(v0sinα)3+(ev0cosα)2
and tanβ=v0sinαev0cosα
or tanβ=tanαe
Topper's Solved these Questions
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEYCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Solved Examples
13 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEYCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Type 1
1 Video
- CENTRE OF MASS, IMPULSE AND MOMENTUMBOOK - DC PANDEYCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - Comprehension type questions
15 Videos
- CIRCULAR MOTIONBOOK - DC PANDEYCHAPTER - CIRCULAR MOTIONEXERCISE - Medical entrances s gallery
19 Videos
Similar Questions
A ball of mass m hits the floor with a speed v0 making an angle of incidence α with the normal. The coefficient of restitution is e. find the speed of the reflected ball and the angle of reflection of the ball.
View SolutionA ball of a mass m hits the floor with as speed v making an angle of incidence θ with the normal. The coefficient of restitution is e. Find the speed of the reflected ball and the angle of reflection of the ball.

View Solution
Knowledge Check
A particle of mass m strikes on ground with angle of incidence 45∘. If coefficient of restitution, e=1√2, find the velociy after impact and angle of reflection.
Atan−1(2)Btan−1(1√2)Ctan−1(√2)Dtan−1(12)Two balls of masses 2m and m are moving with speed 2v0 and v0 towards each other. If the coefficient of restitution e=1/3 , the speed of balls , if collision is head - on
Av03,4v03B2v03,5v03C2v03,4v03Dv03,2v03The first ball of mass m moving with a velocity u collides head on with the second ball of mass m at rest. If the coefficient of restitution is e, the ratio of final velocity of the second ball to the initial velocity of the first ball is
A1−e1+eB1+e1−eC1+e2D1−e2
A particle of mass m strikes a smooth floor with speed u at angle of incidence θ with the normal. The coefficient of resultant is e. Find the magnitude and direction of velocity with which the particle rebounds. Also, find the impulse and loss in K.E.
View SolutionA particle of mass m strikes on ground with angle of incidence 45∘. If coefficient of restitution, e=1√2, find the velociy after impact and angle of reflection.
View SolutionA small ball of mass m collides with as rough wall having coefficient of friction μ at an angle θ with the normal to the wall. If after collision the ball moves with angle α with the normal to the wall and the coefficient of restitution is e, then find the reflected velocity v of the ball just after collision.

View SolutionA particle of mass m strikes a horizontal smooth floor with velocity u making an angle θ with the floor and rebound with velocity v making an angle θ with the floor. The coefficient of restitution between the particle and the floor is e. Then
View SolutionA ball of mass 500 gm moving with speed 2m/s collide to a floor making an angle of 450 with vertical.If coefficient of restitution is 1√3 ,then the angle made by the ball with normal,after collision is
(A) 60∘
(B) 30∘
(C) 45∘
(D) 37∘
View Solution
