Block A has a weight of 3000N and block B has a weight of 50N. Coefficient of friction for A is μk=0.2. Determine the pseed of block A after moves 1m down the plane, starting from rest. Negelect the mass of the cord and pulleys.
The correct Answer is:A, B
If A moves 1 m down the plane and its speed is v, then B will move 2m upwards and its speed will be 2v,
.
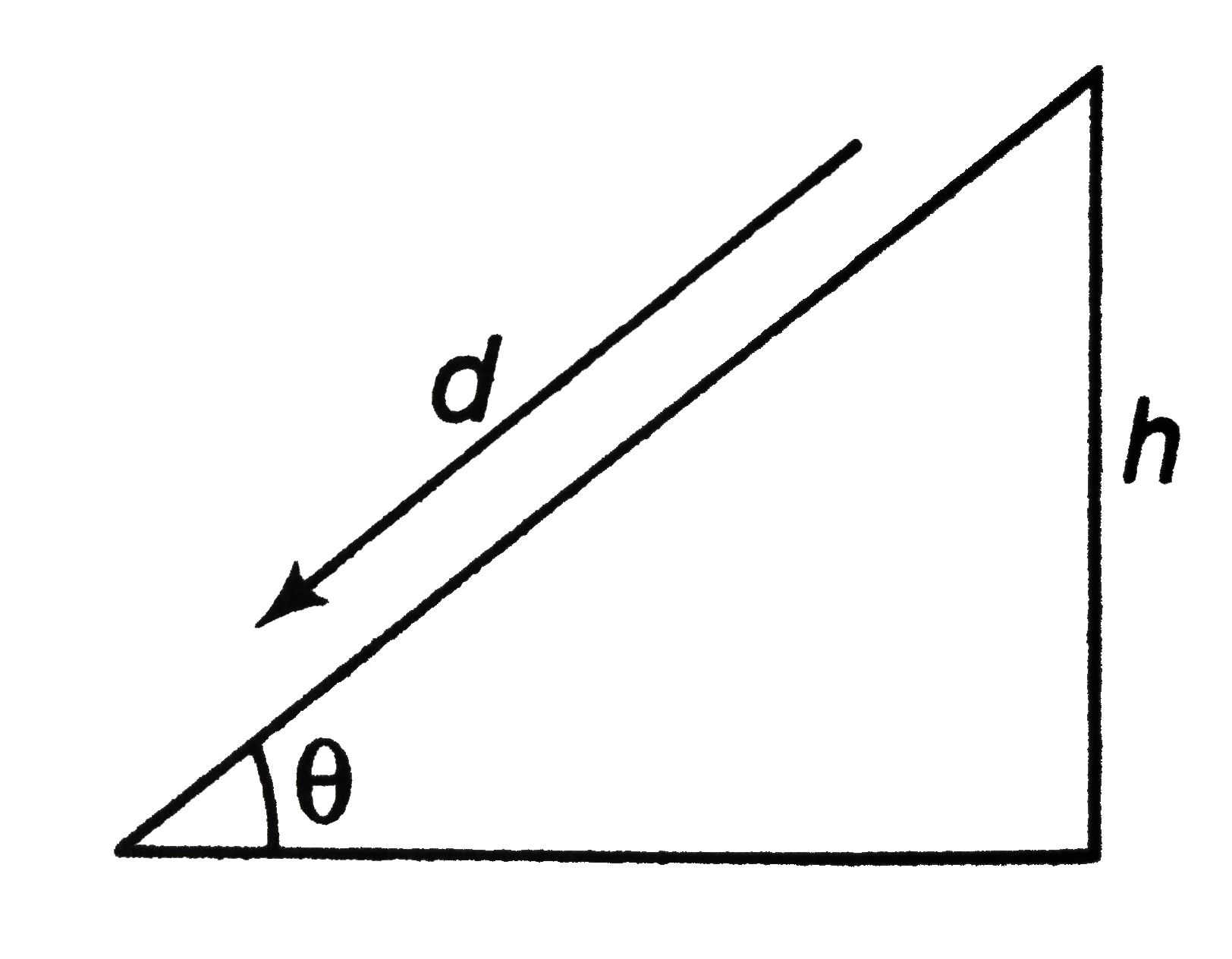Using the equation,
Ei−Ef=Workdo≠aga∈stiction<br>:. 0-[1/2 xx 30 xx v^(2) + 1/2 xx 5 xx (2v)^(2)<br>+ 5 xx 10 xx 2- 30 xx10 xx3/5]<br>=0.2 xx 30 xx 10 xx 4/5 xx1<br>Solv∈gthisequationwe≥t,<br>v = 1.12 m//s
Similar Questions
Block A has a weight of 3000N and block B has a weight of 500N. Determine the distance that A must descend from rest before it obtains a speed of 2.5m/s. Neglect the mass of the cord and pulleys.
. View SolutionBlock A has a weight of 300N and block B has weight 50N. Calculate the distance A must descent form rest before it obtains a speed of 4m/s (Neglect the mass of cord and pulleys). (Takeg=10m/s2).
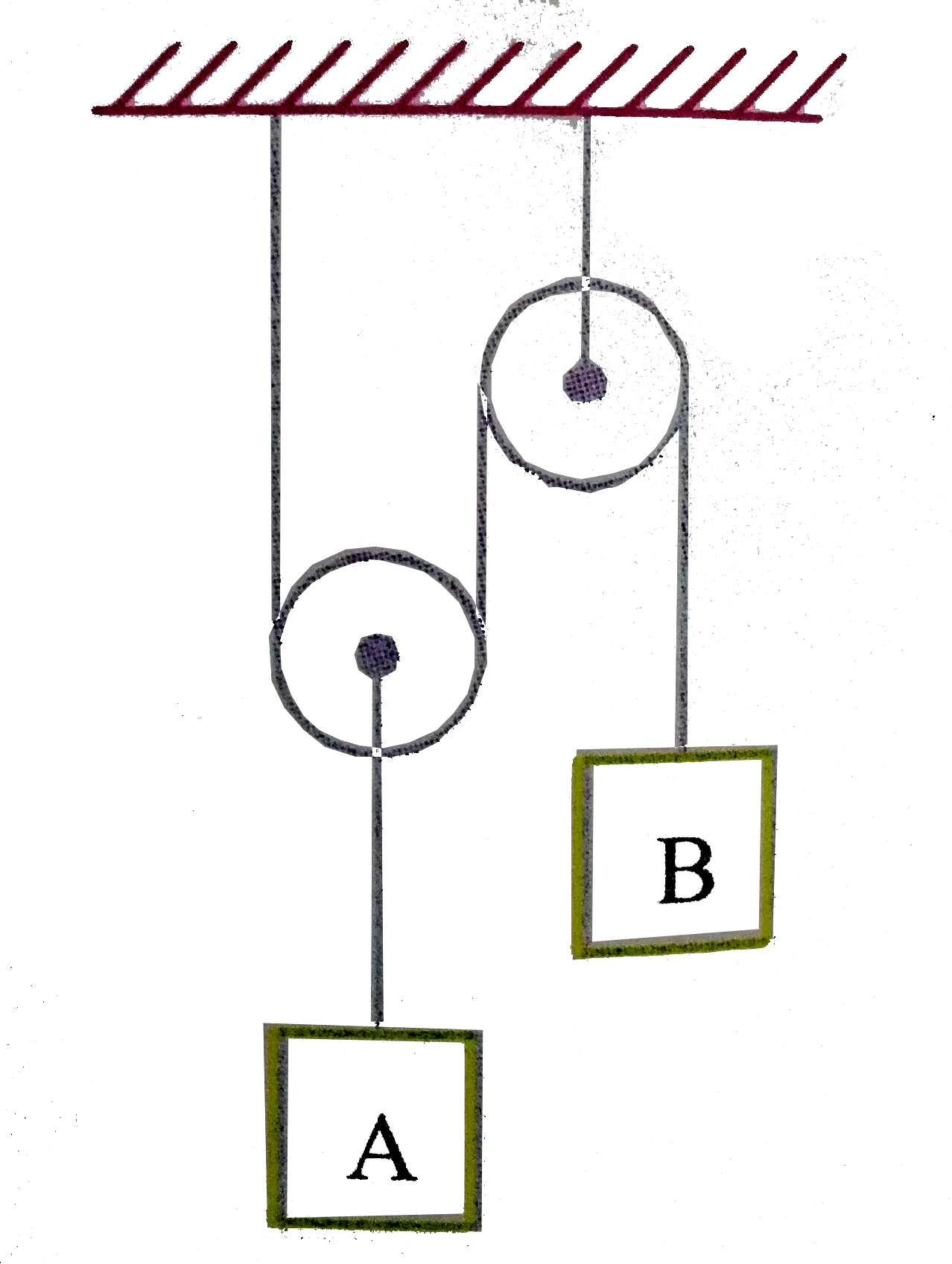.View Solution
Knowledge Check
- Question 1 - Select One
Block A weights 4 N and block B weights 8 N. The coefficient of kinetic friction is 0.25 for all surfaces. The force F to slide B at a constant speed, when A rests on B and moves with it, is
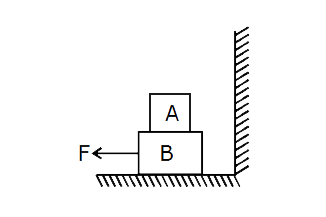A2 NB3 NC4 ND5 N - Question 2 - Select One
A block of mass ''m' is attached with a mass - less spring of force constant k. The block is placed over a rough inclined surface for which the coefficient of friction is μ=3/4. The minimum value of 'M' required so that the block on the inclined plane is at rest (neglect mass of string and pulley).
A5m4B9m20C7m20D3m5 - Question 3 - Select One
A block of mass m sides down an inclined right angled trough .If the coefficient of friction between block and the trough is μk acceleration of the block down the plane is
Ag(sinθ+√2μkcosθ)Bg(sinθ+μkcosθ)Cg(sinθ−√2μkcosθ)Dg(sinθ−μkcosθ)
Block A has a mass of 30kg and block B a mass of 15kg . The coefficient of friction between all surface of contact are μs=0.15 and μs=0.10 Knowing that θ=30∘ and that the magnitude of the force F applied to block A is 250N Determine (a) acceleration of block A and (b) the tension in the rope
View SolutionIf the mass of the block A = 10 kg and the coefficient of static and kinetic friction is 0.2, then the mass of block B to start the motion is
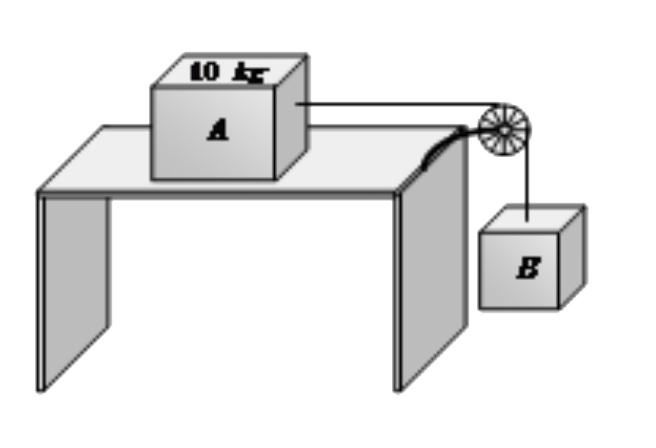
View SolutionBlock B rests on a smooth surface .The coefficient of static friction between A and B is μ=0.4 where F=30N then
Acceleration of lower block is
View SolutionBlock B rests on a smooth surface .The coefficient of static friction between A and B is μ=0.4 where F=30N then
Acceleration of upper block isView SolutionA block of mass m is attached with a massless spring of force constant k. The block is placed over a rough inclined surface for which the coefficient of friction is μ=34. The minimum value of M required to move the block up the plane is (Neglect mass of string, mass of pulley and friction in pulley)
View Solution