A smooth track in the form of a quarter-circle of radius 6 m lies in the vertical plane. A ring of weight 4(N) moves from $P_{1}$ and $P_{2}$ under the action of forces $F_{1}, F_{2}$ and $F_{3}$ . is always towards $P_{2}$ under the action of forces $F_{1}, F_{2}$ and $F_{3}$ Force $F_{1}$ is always towards $P_{2}$ and is always (20) N in maghitude, force $F_{2}$ always acts hotizontally and is always (30 N) in magnitude, force $F_{3}$ always acts tangentially to the track and is of magnitude $(15 - 10 s) N$ , where s is in metre. If the particle has speed $4 m / s$ at $P_{1}$ ,what will its speed be at $P_{2}$ ?

Video Solution

Text Solution

Verified by Experts

The work done by $F (1)$ is
$W_{1} = \int_{P 1}^{P 2} F_{1} cos θ d s$
From figure, $s = R (\frac{π}{2} - 2 θ)$
or $d s = (6 m) d (- 2 θ) = - 12 d θ$
and $F_{1} = 20$ .
At $P_{1}$ , $2 θ = \frac{π}{2} \Rightarrow θ = \frac{π}{4}$
At, $P_{2}, 20 = 0 \Rightarrow θ = 0$
Hence, $W_{1} = - 240 \int_{π / 4}^{0} cos θ d θ$
$= 240 \frac{sin π}{4} = 120 \sqrt{2} J$

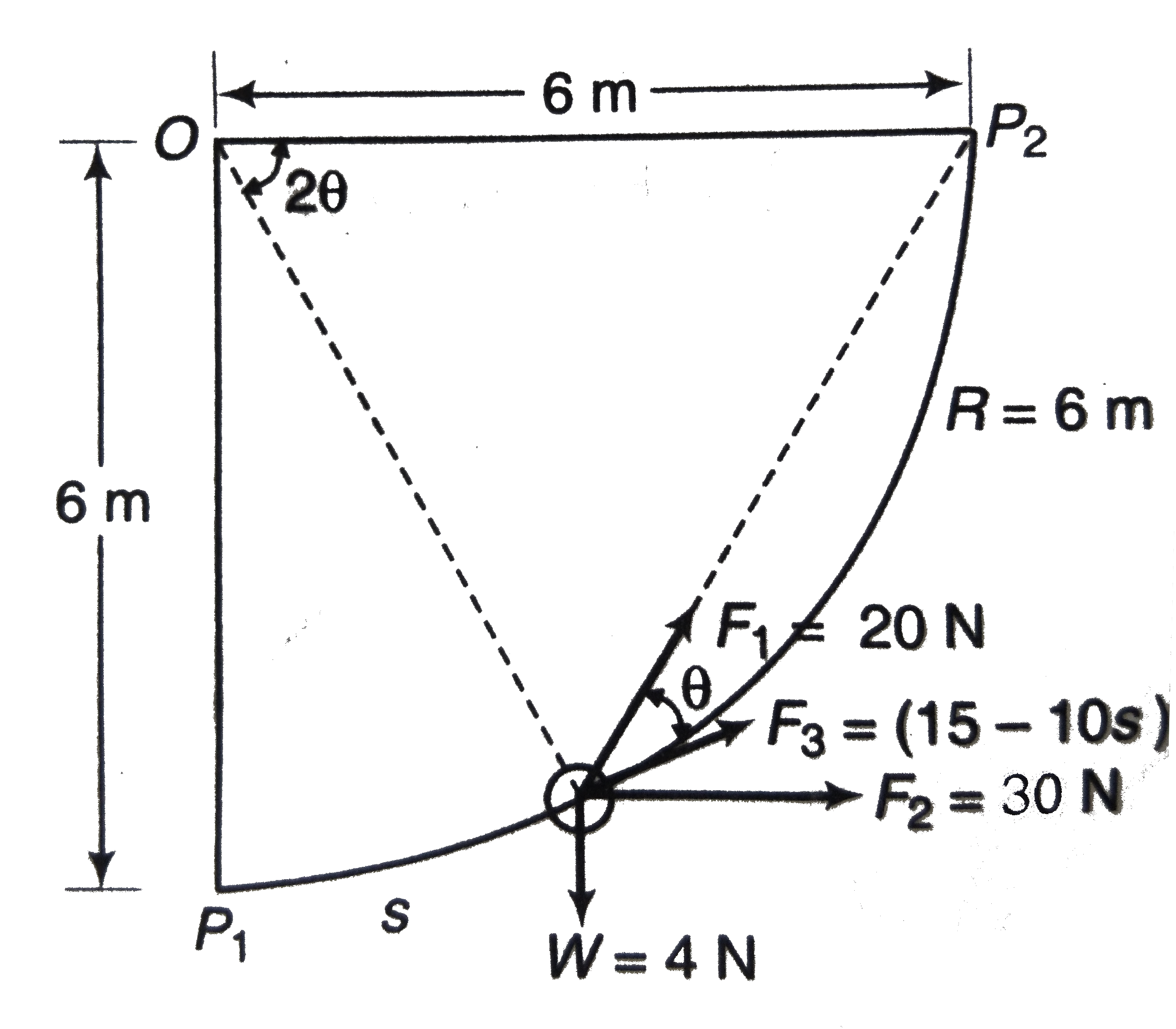
the work done by $F_{3}$ is
$W_{3} = \int F_{3} d s = \int_{0}^{6 (π / 2)} (15 - 10 s) d s, (P_{1} P_{2} = R \frac{π}{2} = \frac{6 π}{2})$
${[15 s - 5 s^{2}]}_{0}^{2} = - 302.8 J$
To calculate the work done by $F_{2}$ and by w, it is convenient to take the projection of the path in the direction of the force. Thus,
$W_{=} (2) F_{2} (O P_{2}) = 30 (6) = 180 J$
$W_{4} = (- w) (P_{1} O) = (- 4) (6) = - 24 J$ (w=weight)
The total work done is , $W_{1} + W_{3} + W_{2} + W_{4} = 23 J$
Then, by the work-energy principle.
$K_{P 2} - K_{P 1} = 23 J$
$= \frac{1}{2} (\frac{4}{9.8}) v_{2}^{2} - \frac{1}{2} (\frac{4}{9.8}) {(4)}^{2} = 23$ .
$v_{2} = 11.3 m / s$ .

Updated on:21/07/2023

|

Class 11 PHYSICS WORK, ENERGY AND POWER

Topper's Solved these Questions

Similar Questions

DC PANDEY-WORK, ENERGY & POWER-Miscellaneous Example

Home
Ask Doubt
Profile