When forces F1 , F2 , F3 are acting on a particle of mass m such that F2 and F3 are mutually prependicular, then the particle remains stationary. If the force F1 is now rejmoved then the acceleration of the particle is
F1/m
F2F3/mF1
(F2−F3)/m
F2/m
The correct Answer is:A
To solve the problem step by step, we can follow these logical steps:
Step 1: Understand the Forces Acting on the Particle
We have three forces acting on a particle of mass m: F1, F2, and F3. The forces F2 and F3 are mutually perpendicular.
Step 2: Condition for the Particle to be Stationary
Since the particle remains stationary, the net force acting on it must be zero. This means:
F1+F2+F3=0
This implies that F1 is balancing the resultant of F2 and F3.
Step 3: Calculate the Resultant of F2 and F3
Since F2 and F3 are perpendicular, we can find their resultant using the Pythagorean theorem:
R=√F22+F23
Thus, we can express F1 in terms of F2 and F3:
F1=R=√F22+F23
Step 4: Remove F1 and Analyze the Situation
Now, if we remove F1, the only forces acting on the particle will be F2 and F3. Since F2 and F3 are not balanced by F1 anymore, the particle will experience a net force equal to the resultant of F2 and F3.
Step 5: Calculate the Acceleration of the Particle
According to Newton's second law of motion, the acceleration a of the particle can be calculated using the formula:
F=ma
Here, the net force F acting on the particle is the resultant of F2 and F3:
F=R=√F22+F23
Thus, we can write:
√F22+F23=ma
From this, we can derive the acceleration a:
a=√F22+F23m
Step 6: Relate the Resultant to F1
Since we established earlier that F1=√F22+F23, we can substitute this back into our equation for acceleration:
a=F1m
Final Answer
Thus, the acceleration of the particle when F1 is removed is:
a=F1m
---
We have three forces acting on a particle of mass m: F1, F2, and F3. The forces F2 and F3 are mutually perpendicular.
Since the particle remains stationary, the net force acting on it must be zero. This means:
F1+F2+F3=0
This implies that F1 is balancing the resultant of F2 and F3.
Since F2 and F3 are perpendicular, we can find their resultant using the Pythagorean theorem:
R=√F22+F23
Thus, we can express F1 in terms of F2 and F3:
F1=R=√F22+F23
Now, if we remove F1, the only forces acting on the particle will be F2 and F3. Since F2 and F3 are not balanced by F1 anymore, the particle will experience a net force equal to the resultant of F2 and F3.
According to Newton's second law of motion, the acceleration a of the particle can be calculated using the formula:
F=ma
Here, the net force F acting on the particle is the resultant of F2 and F3:
F=R=√F22+F23
Thus, we can write:
√F22+F23=ma
From this, we can derive the acceleration a:
a=√F22+F23m
Since we established earlier that F1=√F22+F23, we can substitute this back into our equation for acceleration:
a=F1m
Thus, the acceleration of the particle when F1 is removed is:
a=F1m
Topper's Solved these Questions
- NEWTONS LAWS OF MOTIONBook:A2ZChapter:NEWTONS LAWS OF MOTIONExercise:Linear Momentum And Impulse
Explore 20 Videos
- NEWTONS LAWS OF MOTIONBook:A2ZChapter:NEWTONS LAWS OF MOTIONExercise:Equilibrium Of A Particle
Explore 19 Videos
- MOTION IN TWO DIMENSIONBook:A2ZChapter:MOTION IN TWO DIMENSIONExercise:Chapter Test
Explore 29 Videos
- OSCILLATION AND SIMPLE HARMONIC MOTIONBook:A2ZChapter:OSCILLATION AND SIMPLE HARMONIC MOTIONExercise:Chapter Test
Explore 29 Videos
Similar Questions
Knowledge Check
When forces F1, F2, F3, are acting on a particle of mass m such that F2 and F3 are mutually perpendicular, then the particle remains stationary. If the force F1 is now removed then the acceleration of the particle is
A(a) F/mB(b) F2F3/mF1C(c) (F2−F3)/mD(d) F2/mWhen force →F1,→F2,→F3 are acting on a particle of mass m, the particle remains in equilibrium. If the force →F1 is now removed then the acceleration of the particle is :
A→F1/mB→F1/mC→F2−→F3/mD→F2/mWhen force −→F1,−→F2,−→F3…...−→Fn act on a particle , the particle remains in equilibrium . If −→F1 is now removed then acceleration of the particle is
A−→F1mB−−→F1mC−−→F2+−→F3+.....−→Fn−−→F1mD−→F1m
F1 particle of oxysome
View SolutionFive forces →F1,→F2,→F3,→F4 , and →F5 , are acting on a particle of mass 2.0kg so that is moving with 4m/s2 in east direction. If →F1 force is removed, then the acceleration becomes 7m/s2 in north, then the acceleration of the block if only →F1 is action will be:
View SolutionWhen a force F acts on a particle of mass m, the acceleration of particle becomes a. now if two forces of magnitude 3F and 4F acts on the particle simultaneously as shown in figure, then the acceleration of the particle is
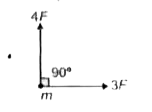
View SolutionTwo forces f1=4N and f2=3N are acting on a particle along positve X−axis and negative y−axis respectively. The resultant force on the particle will be−
View SolutionA particle of mass m is acted upon by a force F=t2−kx . Initially , the particle is at rest at the origin. Then
View Solution

