At the bottom edge of a smooth wall, an inclined plane is kept at an angle of 45∘. A uniform ladder of length l and mass M rests on the inclined plane against the wall such that it is perpendicular to the incline.
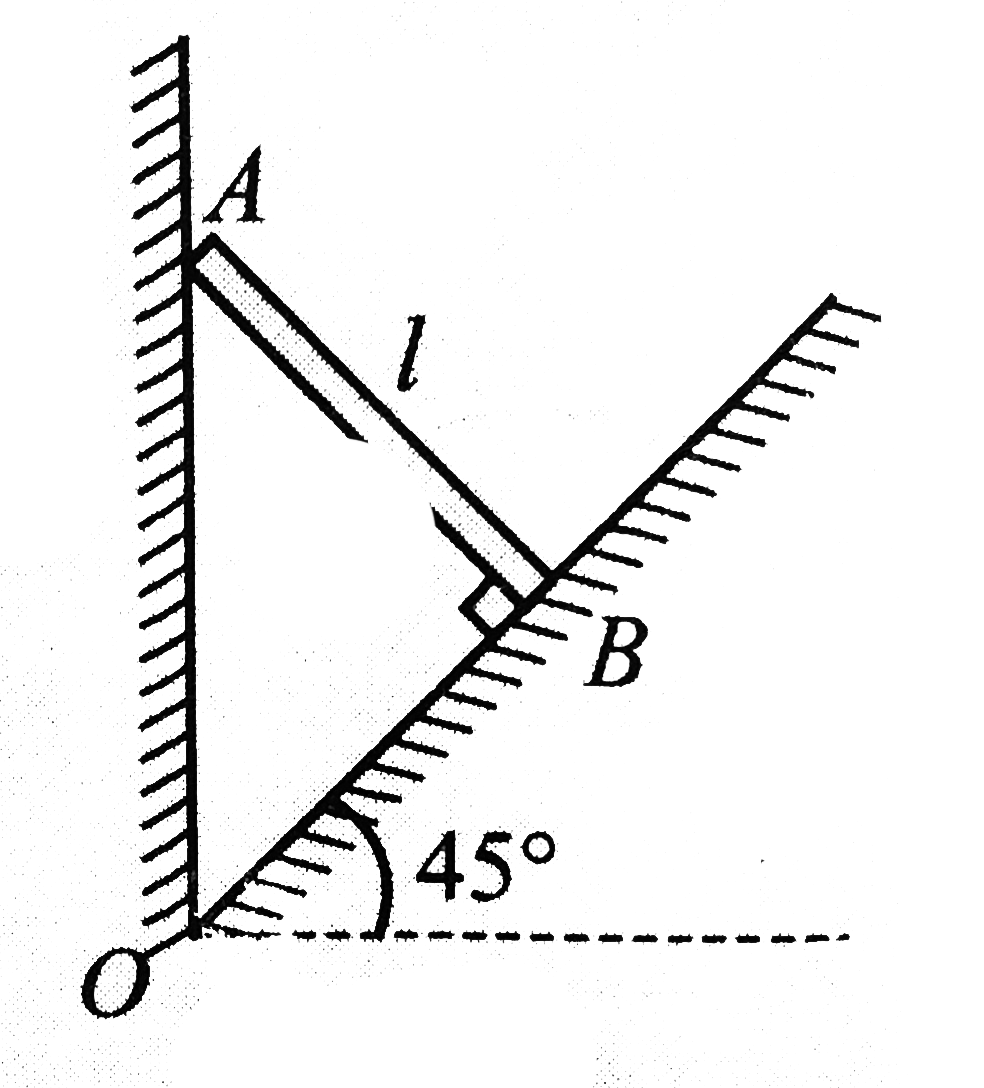
a. If the plane is also smooth, which way will the ladder slide?
b. What is the minimum coefficient of friction necessary so that the ladder does not slip on the incline.
The correct Answer is:A, B, C
(a)N2 and mg pass through G.N1 has has clockwise moment about G , so the ladder has a tendency to slip by rotating clockwise and the force of friction
(f) at B is then up the plane
(b) ∑A=0
∴Fl=mg(12sin45∘)) ...(i)
∑Fv=0
∴mg=N2cos45∘+fsin45∘ ...(ii)
From Eqs.. (i) and (ii), N2=32√2mg
and f=mg(2√2)
or μmin=fN2
=13
Topper's Solved these Questions
- LAWS OF MOTIONBook:DC PANDEYChapter:LAWS OF MOTIONExercise:example
Explore 86 Videos
- LAWS OF MOTIONBook:DC PANDEYChapter:LAWS OF MOTIONExercise:Check point 5.1
Explore 20 Videos
- LAWS OF MOTIONBook:DC PANDEYChapter:LAWS OF MOTIONExercise:Comprehension
Explore 9 Videos
- KINEMATICS 1Book:DC PANDEYChapter:KINEMATICS 1Exercise:INTEGER_TYPE
Explore 15 Videos
- LAWS OF THERMODYNAMICSBook:DC PANDEYChapter:LAWS OF THERMODYNAMICSExercise:Level 2 Subjective
Explore 18 Videos
Similar Questions
A block is released on an smooth inclined plane of inclination θ. After how much time it reaches to the bottom of the plane?

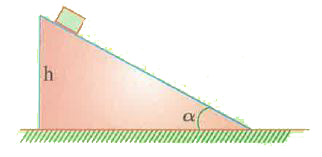
View SolutionA mass m slides down a fixed plane inclined at an angle a to the horizontal plane after covering the entire length of the inclined plane. The height of the inclined plane is h and the coefficient of friction over both surfaces is μ.
View Solution
Knowledge Check
A body takes twice the time to slides down a rough inclined plane at 45° to an identical smooth inclined plane. What is the coefficient of friction of rough plane?
A0.75B0.5C0.25D0.15A ladder of length l and mass m is placed against a smooth vertical wall, but the ground is not smooth. Coefficient of friction between the ground and the ladder is μ. The angle θ at which the ladder will stay in equilibrium is
Aθ=tan−1(μ)Bθ=tan−1(2μ)Cθ=tan−1(μ2)Dnone of theseA uniform ladder rests in limiting equilibrium, its lower end on a rough horizontal plae and its upper end against a smooth vertical wall. If θ is the engle of inclination of the ladder to the vertical wall and μ is the coefficient of friction then tanθ is equal to
AμB2μC3μ/2Dμ+1
A body is kept on a smooth inclined plane having an inclination of 1 in x. Then,
View SolutionAn object is kept on a smooth inclined plane of height 1 unit and length l units. The horizontal acceleration to be imparted to the inclined plane so that the object is stationary relative to the incline is
View SolutionA body kept on a smooth inclined plane having inclination 1 in x will remain stationary relative to the inclined plane if the plane is given a horizontal accelertion equal to
View SolutionA smooth inclined plane is inclined at an angle θ with the horizontal. A body starts from rest and slides down the inclined surface. The time taken by the body to reach the bottom is
View SolutionAn inclined plane is inclined at an angle θ with the horizontal. A body of mass m rests on it, if the coefficient of friction is μ, then the minimum force that has to be applied to the inclined plane to make the body just move up the inclined plane is
View Solution

