In the figure shown ,find :(g=10m/s2)

(a) acceleration of 1kg,2kg and 3kg blocks and
(b) tension T1 and T2.
P12T1=2T2
∴T1=T2 …(i)
1kgT2=(1)(a) …(ii)
2kgT1−20=2(ar−a2) …(iii)
3kg30−T1=3(ar+a2) …(iv)
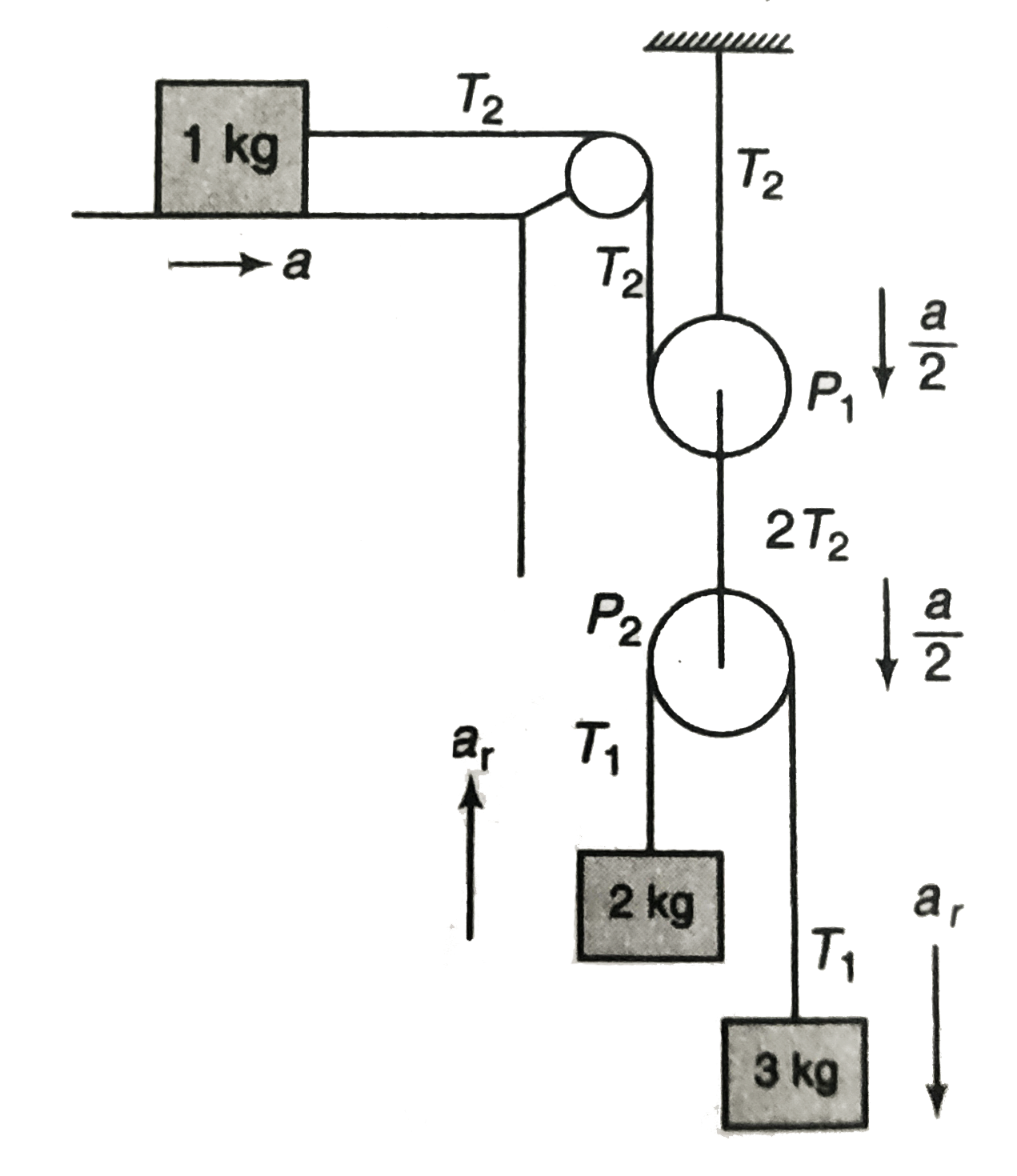
On solving these equation, we get
T1=T2=12011N
a1=a=12011m/s2
a2=ar−a2=−5011m/s2
or a2=5011m/s2 (downwards)
a3=ar+a2=7011m/s2 (downwards)
Topper's Solved these Questions
- LAWS OF MOTIONBook:DC PANDEYChapter:LAWS OF MOTIONExercise:Objective Question
Explore 32 Videos
- LAWS OF MOTIONBook:DC PANDEYChapter:LAWS OF MOTIONExercise:Comprehension
Explore 9 Videos
- LAWS OF MOTIONBook:DC PANDEYChapter:LAWS OF MOTIONExercise:Exercise 8.5
Explore 2 Videos
- KINEMATICS 1Book:DC PANDEYChapter:KINEMATICS 1Exercise:INTEGER_TYPE
Explore 15 Videos
- LAWS OF THERMODYNAMICSBook:DC PANDEYChapter:LAWS OF THERMODYNAMICSExercise:Level 2 Subjective
Explore 18 Videos
Similar Questions
Knowledge Check
In the figure shown, m1 = 10kg, m2 = 6kg, m3 = 4kg. If T3 = 40 N, T2 = ?
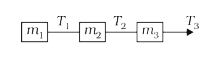 A13 NB32 NC25 ND35 N
A13 NB32 NC25 ND35 NIn the arrangement as shown, tension T2 is -
(g=10m/s2)
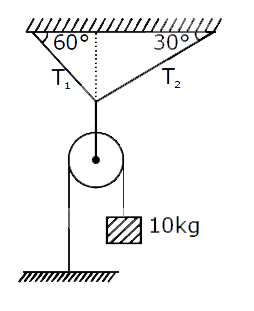 A50 NB100 NC50√3ND100√3N
A50 NB100 NC50√3ND100√3NIn the adjacent figure, masses of A,B and C are 1kg,3kg and 2kg respectively. Find
(a) the acceleration of the system and
(b) tension in the strings.
Neglect friction.(g=10m/s2)
 A2.1m/s2 , T1=4.56NB4.1m/s2 , T1=2.56NC4.1m/s2 , T1=4.56ND4.1m/s2 , T1=14.56N
A2.1m/s2 , T1=4.56NB4.1m/s2 , T1=2.56NC4.1m/s2 , T1=4.56ND4.1m/s2 , T1=14.56N
In the arrangement as shown, tension T2 is (g=10m/s2)
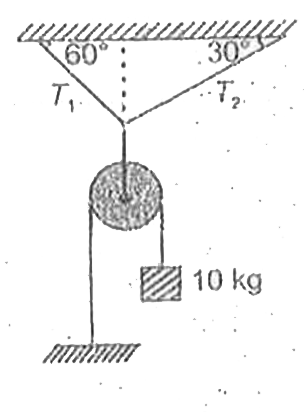
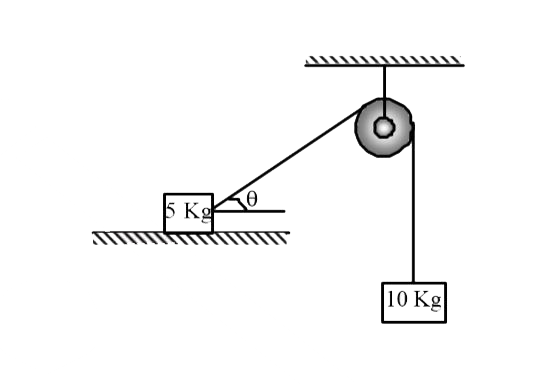
View SolutionIn the arrangment shown pulley is ideal and string is massless. 5kg block is moving on the smooth surface. Whenθ is 37∘, then acceleration of 5kg and 10 kg blocks are a1 and a2 while tension in string is T then :
(g=10m/s2):
View SolutionIn the figure shown, find acceleration of the system and tenslons T1,T2andT3(Take=10m/s2)
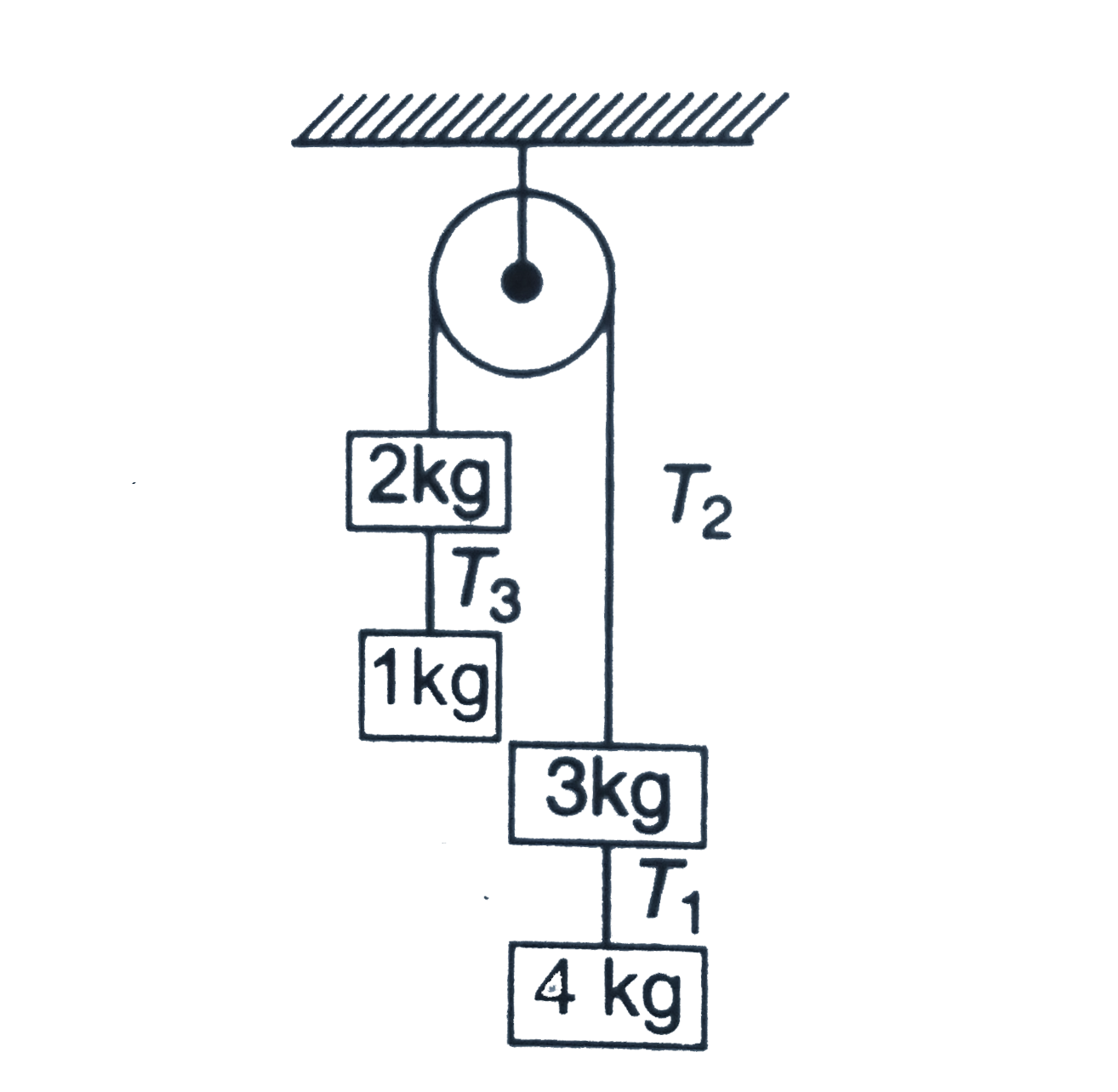
View Solutionin the figure shown all surface are smooth. Find
(a)acceleration of all the blocks,
(b) net force on4kg and 10kg blocks and ,
( c) force acting between 4kg and 10kg blocks.

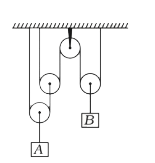
View SolutionIn figure shown if mA=20 kg and mB=80 kg. The acceleration of block A if the system is set free to move is βm/s2 . Find the value of β . (Take g=10ms−2)
View Solution



