A sphere of mass 1kg rests at one corner of a cube. The cube is moved with a velocity v=(8tˆi−2t2)ˆj, where tis time in second . The force by sphere on the cube at t=1s is (g=10m/s−2) [figure shown vertical plane of the cube]
![A sphere of mass 1 kg rests at one corner of a cube. The cube is moved with a velocity v =(8 t hat(i) - 2t^(2)) hat(j), where tis time in second . The force by sphere on the cube at t = 1 s is (g = 10 m//s^(-2)) [figure shown vertical plane of the cube]](https://d10lpgp6xz60nq.cloudfront.net/physics_images/DCP_V01_C08_E01_107_Q01.png)
8N
10N
20N
6N
The correct Answer is:B
a=dvdt=(8ˆi−4tˆj)
At 1sFnet=ma=(1)(8ˆi−4ˆj)=(8ˆi−4ˆj)
=W+F
where F=force on cube
∴F=(8ˆi−4ˆj)−w
=(8ˆi−4ˆj)−(−10ˆj)
=(8ˆi+6ˆj)
or |F|=√(8)2+(6)2
=10N
Topper's Solved these Questions
- LAWS OF MOTIONBook:DC PANDEYChapter:LAWS OF MOTIONExercise:Objective Question
Explore 32 Videos
- LAWS OF MOTIONBook:DC PANDEYChapter:LAWS OF MOTIONExercise:Comprehension
Explore 9 Videos
- LAWS OF MOTIONBook:DC PANDEYChapter:LAWS OF MOTIONExercise:Exercise 8.5
Explore 2 Videos
- KINEMATICS 1Book:DC PANDEYChapter:KINEMATICS 1Exercise:INTEGER_TYPE
Explore 15 Videos
- LAWS OF THERMODYNAMICSBook:DC PANDEYChapter:LAWS OF THERMODYNAMICSExercise:Level 2 Subjective
Explore 18 Videos
Similar Questions
A sphere of mass 0.5 kg rests at one corner of a cube. The cube is moved with velocity v=8ˆi−2t2ˆj where t is time in seconds. Find the magnitude of force by sphere on the cube at t=1 s is (figure shown vertical plane of the cube g=10m/s2)
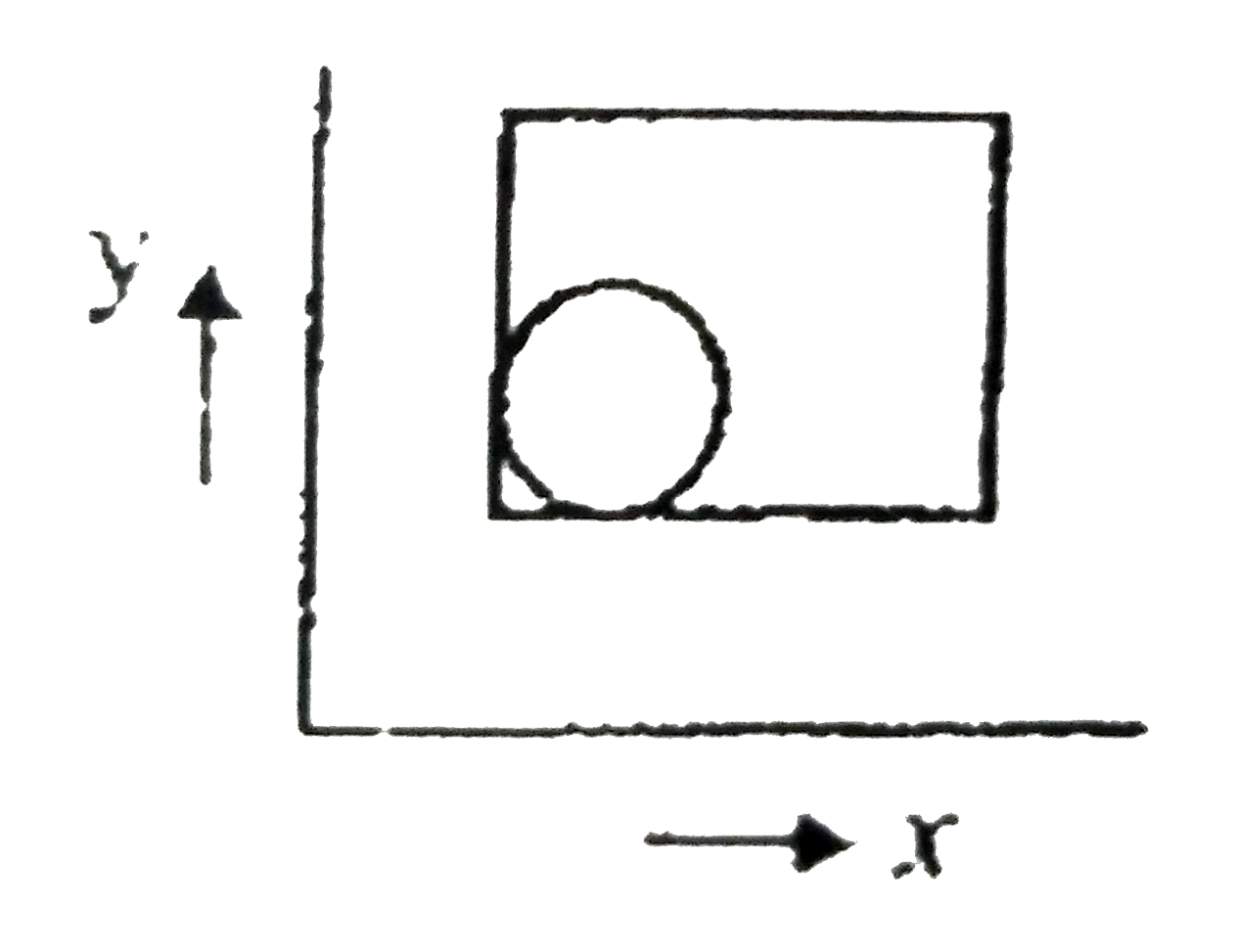
View SolutionA solid sphere of mass of 2kg rests inside a cube as shown The cube is moving with ve-locity →v=(5tˆi+2tˆj)ms−1 where 't' is in sec and 'v' is in m/s What force does sphere exert on cube
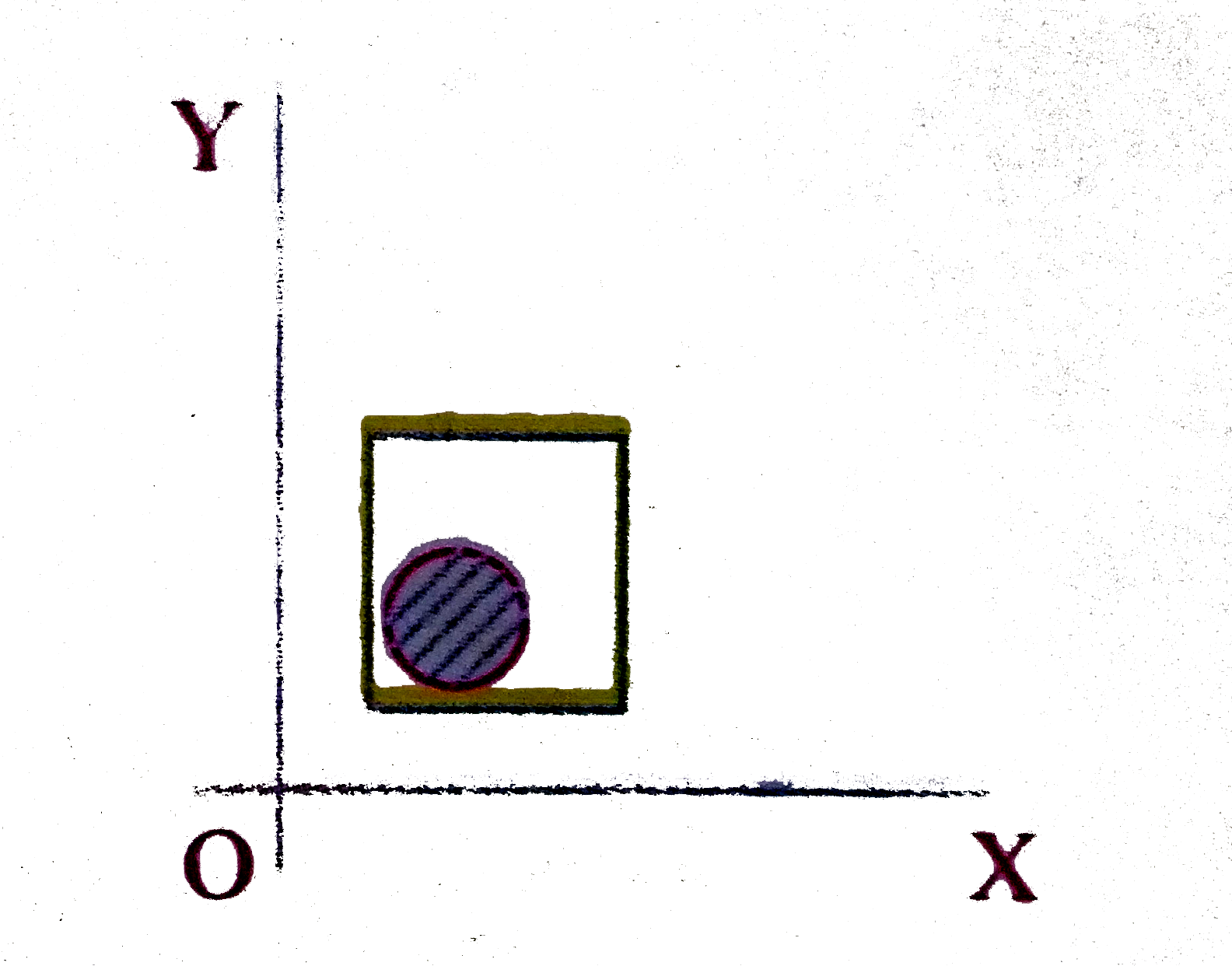 .
.
View Solution
Knowledge Check
A soild block of mass 2 kg is resting inside a cube as shown in the figure .The cube is moving with a veocity v=5tˆi+2ˆjm/s Here , t is is time in second the block is at rest with respect to the cube and cefficient of frision between the surface of ube and block is 0.6 then ,[take g=10m/s2]
 Aforce of friction acting on the block is 10 NBforce of friction acting on the block is 4 NCthe total force exerted by the block on the cube is 10√5NDa,c
Aforce of friction acting on the block is 10 NBforce of friction acting on the block is 4 NCthe total force exerted by the block on the cube is 10√5NDa,cA projectile is given an initial velocity of (ˆi+2ˆj)m/s, where ˆi is along the ground and ˆj is along the vertical . If g=10m/s2, the equation of its trajectory is :
Ay=x−5x2By=2x−5x2C4y=2x−5x2D4y=2x−25x2Velocity of a particle moving in a curvilinear path varies with time as v=(2tˆi+t2ˆk)m/s. Here t is in second. At t=1 s
Aacceleration of particle is 8m/s2Btangential acceleration of particle is 6√5m/s2Cradial acceleration of particle is 2√5m/s2Dradius of curvature to the path is 5√52m
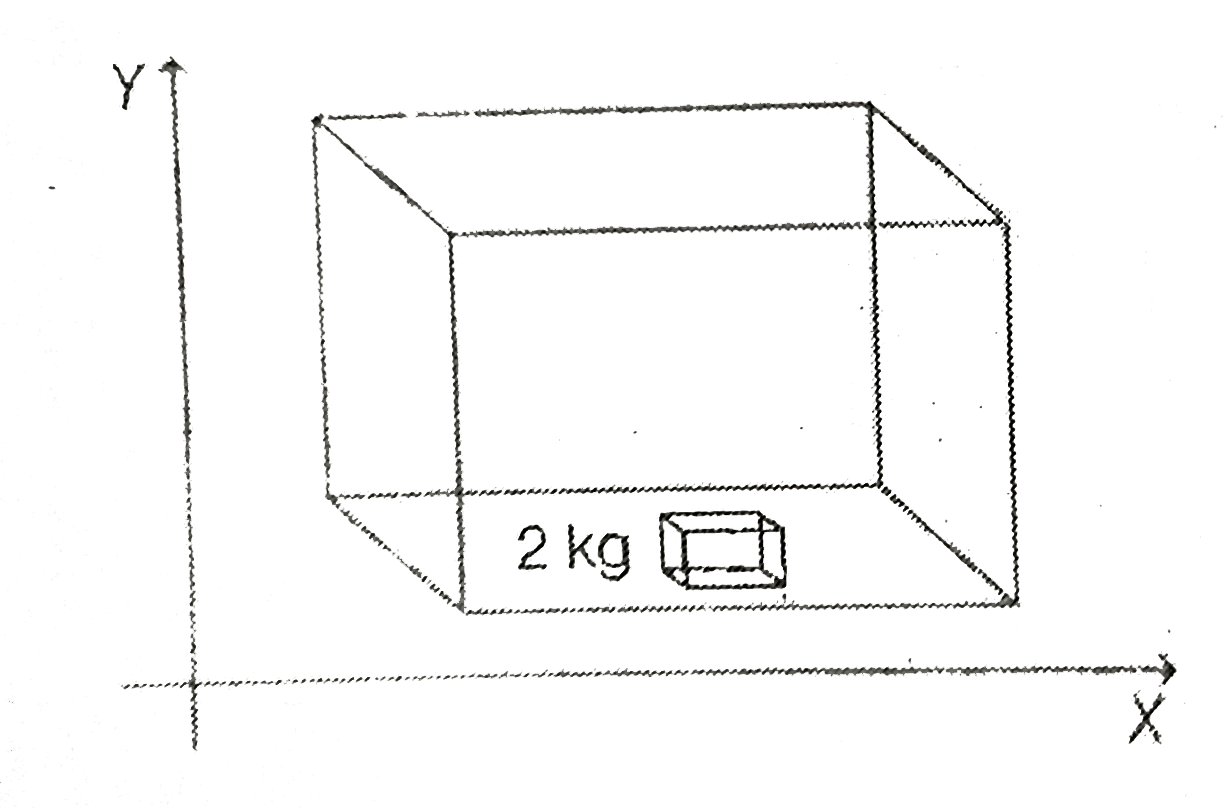
A solid sphere of mass 2 kg is resting inside a cube as shown in fig. The cube is moving with a velocity →v=(5tˆi+2tˆj)ms−1. Here t is time in seconds. All surface are smooth. The sphere is at rest with respect to the cube. What is the total force (in N) exerted by the sphere on the cube?

View SolutionThe position vector of a particle changes with time according to the relation →r(t)=15t2ˆi+(4−20t2)ˆj What is the magnitude of the acceleration at t = 1?
View SolutionA particle of mass 1 kg moves in a circular path of radius 1 m such that its speed varies with time as per equation v=3t2m/s where time t is in seconds. The power delivered by the force acting on the paritcle at t=1s, is :−
View SolutionA solid block of mass 2kg is resting inside a cube shown in figure The cube is moving with a velocity ˆv=5ˆi+2ˆjms−1 If the coefficient of friction between the surface of cube and block is 0.2 then the force of friction between the block and cube is

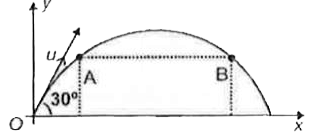
View SolutionA particle is thrown with a velocity of u m/s. it passes A and B as shown in figure at time t1=1 s andt2=3 s . The value of u is (g = 10 m/s2)
View Solution

