The rod shown in figure has a mass of 2kg and length 4m. In equilibrium, find the hinge force (or its two component) acting on the rod and tension in the string. Tage g=10m/s2,sin37∘=35 and cos37∘=45

The correct Answer is:A, B, C
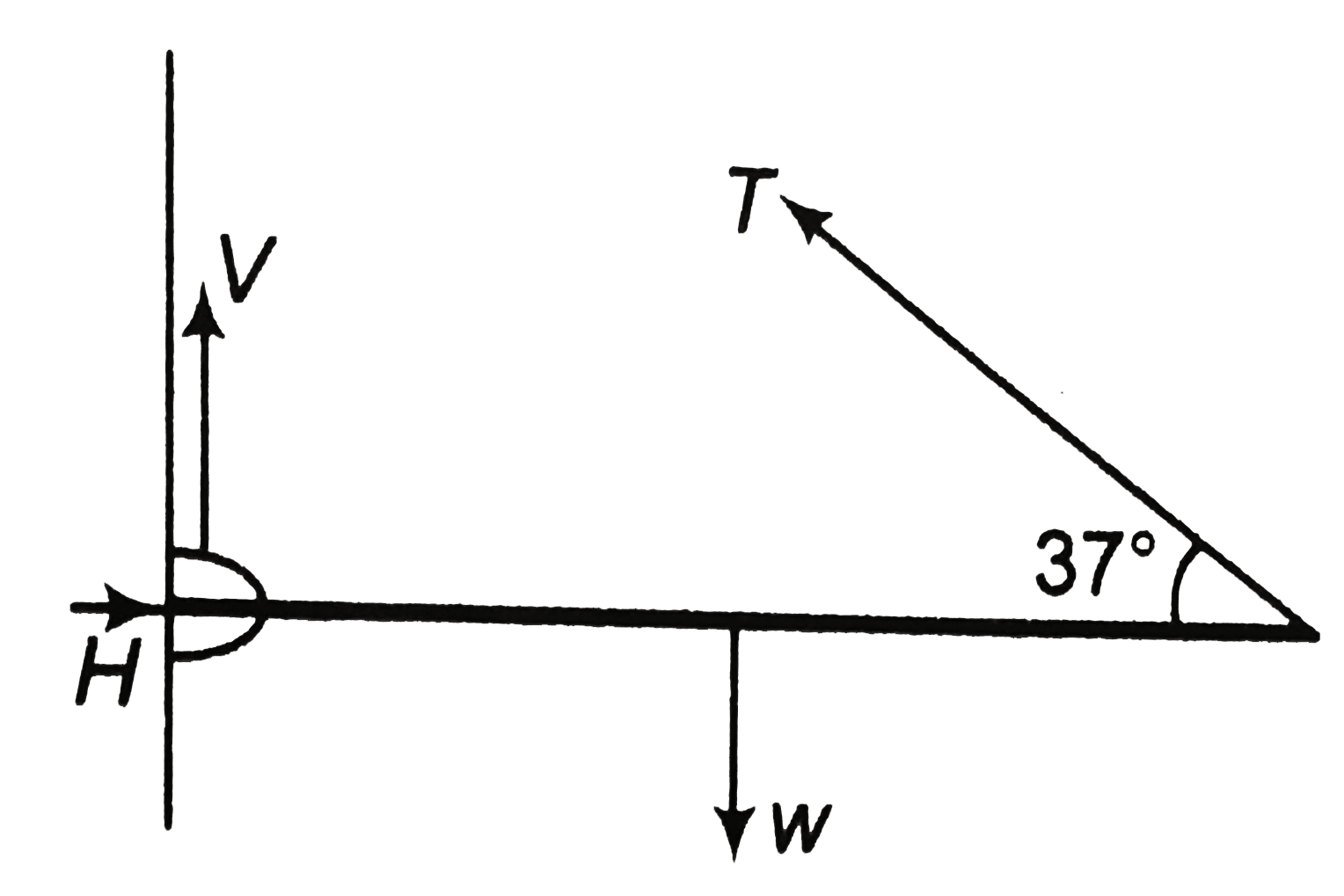
In the figure , only those forces which are acting on the rod has been shown. Here H and V are horizontal and vertical components of the hinge force.
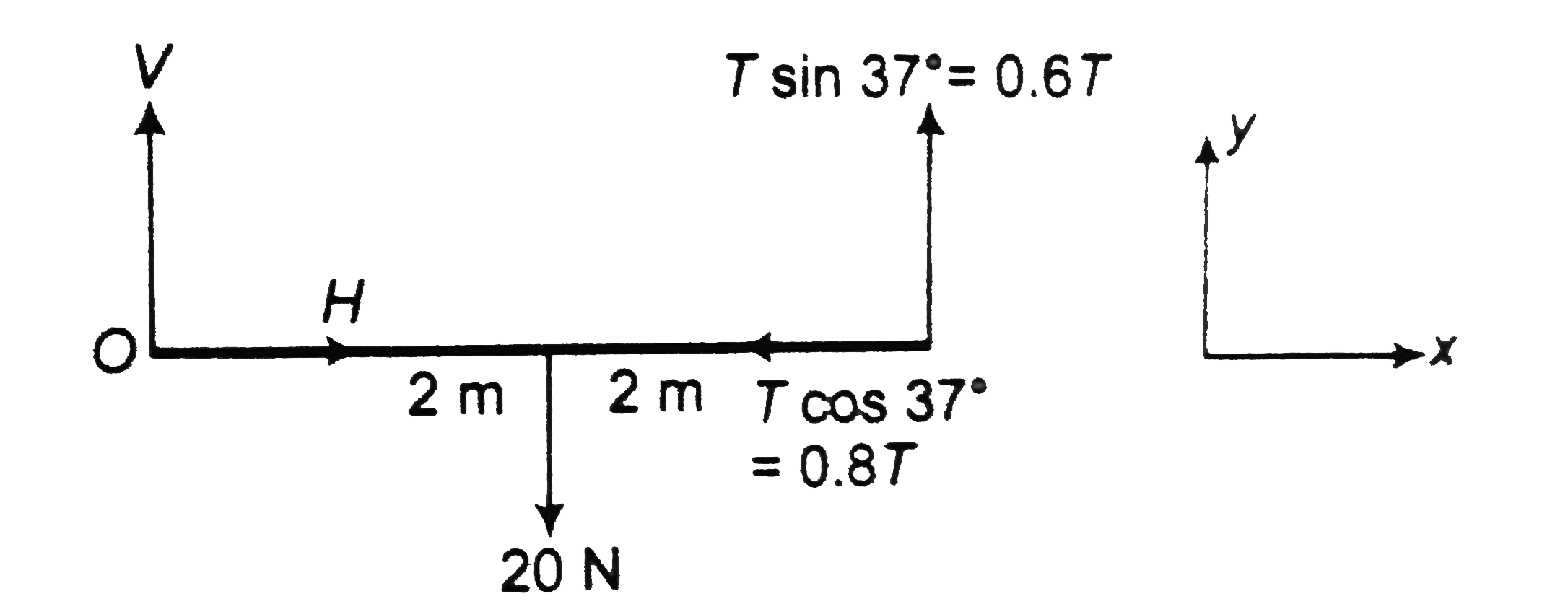
∑Fx=0⇒H−0.8T=0 ...(i)
∑FY=0⇒V+0.6T−20=0 ...(ii)
∑π0=0
⇒ Clockwire torque of 20N=anticlock-wire torque of 0.6T.
All other forces(H,Vand0.8T pass through O, hence their torque are zero).
20×2=0.6T×4 ...(iii)
Solving these three equations, we get
T=16.67N,
H=13.33N
and V=10N
Hing force (F)
F=√13.332+(10)2=16.67N
tanθ=1013.33
θ=tan−1(1013.33)=37∘
Similar Questions
Knowledge Check
A uniform rod of mass m and length L is suspended with two massless strings as shown in the figure. If the rod is at rest in a horizontal position the ratio of tension in the two strings T1T2 is:
 A1:1B1:2C2:1D4:3
A1:1B1:2C2:1D4:3A uniform rod of mass m and length L is suspended with two massless strings as shown in figure. If the rod is at rest in a horizontal position the ratio of tension in the two strings T1/T2 is
 A1:1B1:2C2:1D4:3
A1:1B1:2C2:1D4:3A uniform rod of mass m and length l is hanged by two stirngs as shown in figure. Suddenly one string is cut. The tension in other string at this instant is
 A4MgBMg6CMg3DMg4
A4MgBMg6CMg3DMg4
A particle Is projected at point 'A' with initial velocity 5m/s at an angle θ=37∘ with the vertical y axis. A strong horizontal wind gives the particle a constant horizontal acceleration 6m/s2 in the x direction. If the particle strikes the ground at a point directly under its released position, determine the height 'h' of point A. The downward acceleration is taken as the constant
g=10m/s2(take sin37∘=35,cos37∘=45)

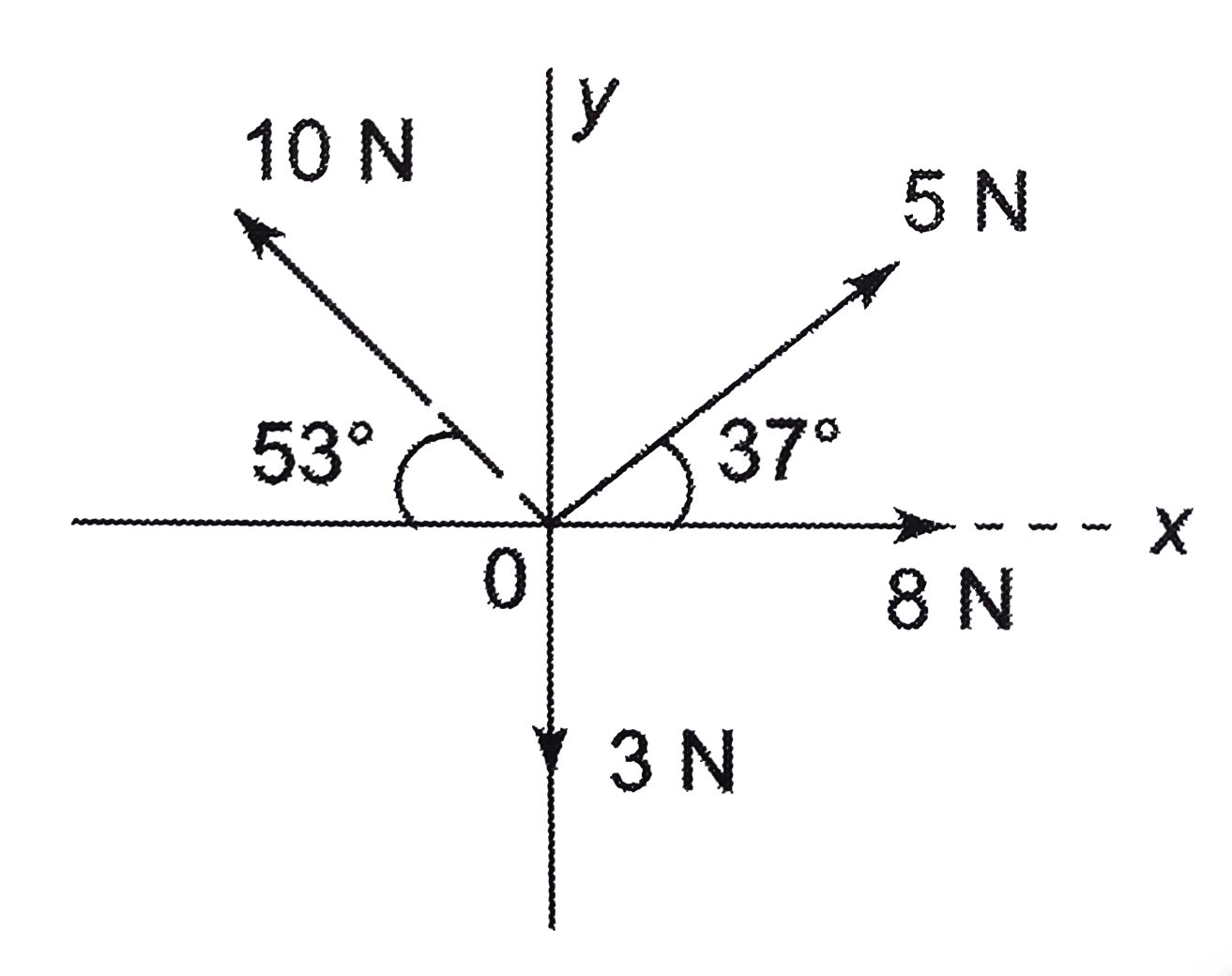
View SolutionFind the resultant of the following forces.
[sin37∘=35,cos37∘=45,sin53∘=45,cos53∘=35]
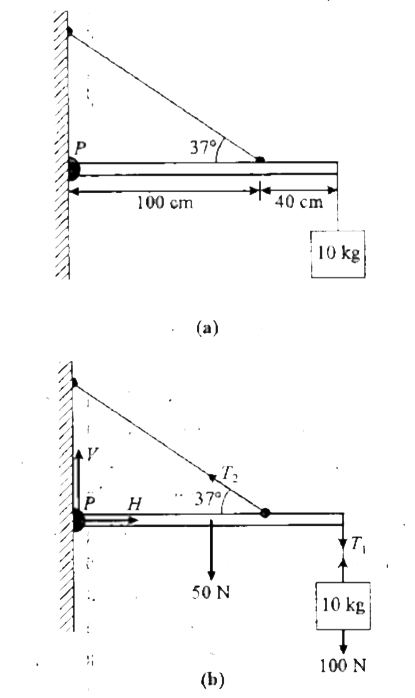
View SolutionFor the uniform 5 kg beam shown in figure-2.41(a), how large is the tension in the supporting cable and what are the components of the force exerted by the hinge on the beam ? Take g=10m/s2
View SolutionA uniform rod of mass m and length l is in equilibrium under the action of constraint forces, gravity and tension in the string. Find the

a. frictional force acting on the rod.
b. tension in the string.
c. normal reaction on the rod.
Now, the string is cut. Find the
d. angular acceleratiion of the rod just after the string is cut.
e. normal reaction on the rod just after the string is cut.
View SolutionA uniform rod of length 1m and mass 2kg is suspended. Calculate tension T (in N) in the string at the instant when the right string snaps (g=10m/s2).

View Solution

