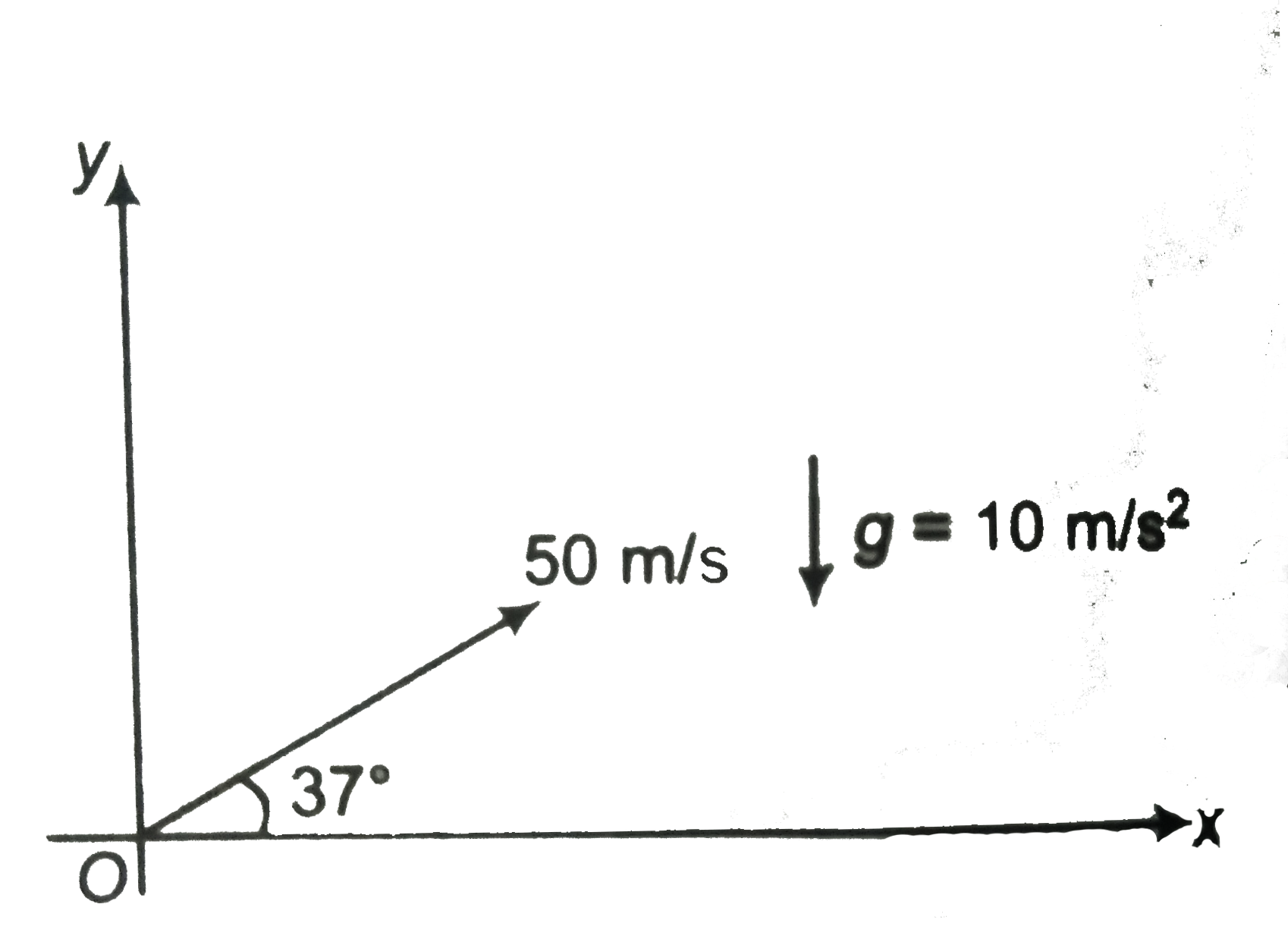
A particle is projected with a velocity of 50 m/s at 37∘ with horizontal. Find velocity, displacement and co-ordinates of the particle (w.r.t. the starting point) after 2 s.
Given, g=10m/s2,sin37∘=0.6andcos37∘=0.8.
(40ˆi+10ˆj)m/s x=80mandy=80m
(40ˆi+10ˆj)m/s x=20mandy=40m
(40ˆi+10ˆj)m/s x=80mandy=40m
(40ˆi+20ˆj)m/s x=80mandy=40m
The correct Answer is:C
In the given problem,
u=(50cos37∘)ˆi+(50sin37∘)ˆj
=(40ˆi+30ˆj)m/s
a=(−10ˆj)m/s2
t=2s
v=u+at
=(40ˆi+30ˆj)+(−10ˆj)(2)
=(40ˆi+10ˆj)m/s
s=ut+12at2
=(40ˆi+30ˆj)(2)+12(−10ˆj)(2)2
=(80ˆi+40ˆj)m
Coordinates of the particle are
x=80 m and y= 40m .
Topper's Solved these Questions
- PROJECTILE MOTIONBOOK - DC PANDEYCHAPTER - PROJECTILE MOTIONEXERCISE - Example Type 1
1 Videos
- PROJECTILE MOTIONBOOK - DC PANDEYCHAPTER - PROJECTILE MOTIONEXERCISE - Example Type 2
1 Videos
- MOTION IN A PLANEBOOK - DC PANDEYCHAPTER - MOTION IN A PLANEEXERCISE - (C )Medical entrances gallery
32 Videos
- PROPERTIES OF MATTERBOOK - DC PANDEYCHAPTER - PROPERTIES OF MATTEREXERCISE - Integer
8 Videos
Similar Questions
A particle is projected from ground with velocity 50m/s at 37∘ from horizontal. Find velocity and displacement after 2 s. sin37∘=35.
View SolutionA particle is projected with a velocity 10 m//s at an angle 37∘ to the horizontal. Find the location at which the particle is at a height 1 m from point of projection.
View Solution
Knowledge Check
A particle is projected with velocity of 10ms at an angle of 15° with horizontal.The horizontal range will be(g=10ms2)
A10mB5mC2.5mD1mA projectile is projected with the initial velocity (6i+8j)m/s. The horizontal range is (g=10m/s2)
A96mB960mC9.6mD4.8m
A particle is projected from ground with velocity 40(√2)m/sat45∘. Find
(a) velocity and
(b) displacement of the particle after 2 s. (g=10m/s2)
View SolutionA particle is projected with velocity 20√2m/s at 45∘ with horizontal. After 1s(g=10m/s2) match the following table
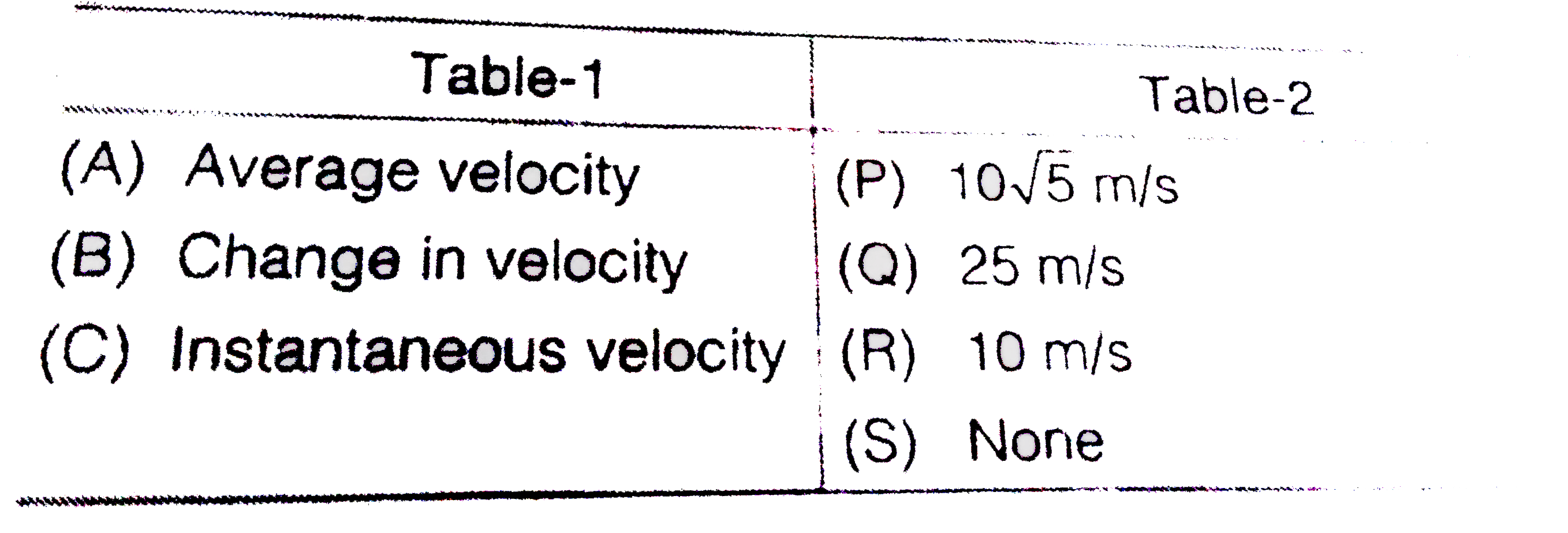
View SolutionA particle is projected vertically upwards with an initial velocity of 40m/s. Find the displacement and distance covered by the particle in 6s. Take g=10m/s2.
View SolutionA particle is thrown with a velocity 10m/s and its horizontal range is 5m. Find angle/angles of the projection.
View SolutionA particle is projected with a velocity of 10√2m/s at an angle of 45∘ with the horizontal. Find the interval between the moments when speed is √125m/s(g=10m/s2)
View SolutionA particle of mass 1 kg is projected at an angle of 30∘ with horizontal with velocity v = 40 m/s . The change in linear momentum of the particle after time t = 1 s will be (g = 10 m/s2)
View Solution
