Two particles A and B start moving simultaneously along the line joining them in the same direction with acceleration of 1m/s2and2m/s2 and speeds 3m/sand1m/s respectively. Initially, A is 10 m behind B. What is the minimum distance between them?
To solve the problem of finding the minimum distance between particles A and B, we can follow these steps:
Step 1: Understand the Initial Conditions
- Particle A has an initial velocity uA=3m/s and an acceleration aA=1m/s2.
- Particle B has an initial velocity uB=1m/s and an acceleration aB=2m/s2.
- Initially, particle A is 10 meters behind particle B.
Step 2: Set Up the Equations for Final Velocities
To find the time when the distance between them is minimized, we need to set their final velocities equal to each other:
vA=uA+aAt=vB=uB+aBt
Substituting the known values:
3+1t=1+2t
Step 3: Solve for Time
Rearranging the equation:
3−1=2t−1t2=t
Thus, t=2s.
Step 4: Calculate the Displacements of Both Particles
Now, we calculate the displacement of both particles after 2 seconds.
For particle A:
SA=uAt+12aAt2=3(2)+12(1)(22)=6+2=8m
For particle B:
SB=uBt+12aBt2=1(2)+12(2)(22)=2+4=6m
Step 5: Calculate the Minimum Distance
The initial distance between A and B is 10 m. After 2 seconds, the new positions of A and B can be expressed as:
- Position of A after 2 seconds: SA=8m
- Position of B after 2 seconds: SB=6m
The minimum distance Dmin between them is given by:
Dmin=Initial distance−(SA−SB)=10−(8−6)=10−2=8m
Final Answer
The minimum distance between particles A and B is 8m.
---
- Particle A has an initial velocity uA=3m/s and an acceleration aA=1m/s2.
- Particle B has an initial velocity uB=1m/s and an acceleration aB=2m/s2.
- Initially, particle A is 10 meters behind particle B.
To find the time when the distance between them is minimized, we need to set their final velocities equal to each other:
vA=uA+aAt=vB=uB+aBt
Substituting the known values:
3+1t=1+2t
Rearranging the equation:
3−1=2t−1t2=t
Thus, t=2s.
Now, we calculate the displacement of both particles after 2 seconds.
SA=uAt+12aAt2=3(2)+12(1)(22)=6+2=8m
SB=uBt+12aBt2=1(2)+12(2)(22)=2+4=6m
The initial distance between A and B is 10 m. After 2 seconds, the new positions of A and B can be expressed as:
- Position of A after 2 seconds: SA=8m
- Position of B after 2 seconds: SB=6m
Dmin=Initial distance−(SA−SB)=10−(8−6)=10−2=8m
The minimum distance between particles A and B is 8m.
Topper's Solved these Questions
- KINEMATICSBook:DC PANDEYChapter:KINEMATICSExercise:Subjective
Explore 51 Videos
- KINEMATICSBook:DC PANDEYChapter:KINEMATICSExercise:More Than One Correct
Explore 6 Videos
- KINEMATICSBook:DC PANDEYChapter:KINEMATICSExercise:Assertion And Reason
Explore 12 Videos
- GRAVITATIONBook:DC PANDEYChapter:GRAVITATIONExercise:(C) Chapter Exercises
Explore 45 Videos
- KINEMATICS 1Book:DC PANDEYChapter:KINEMATICS 1Exercise:INTEGER_TYPE
Explore 15 Videos
Similar Questions
Car A and car B start moving simultaneously in the same direction along the line joining them. Car A with a constant acceleration a = 4 m/s2 , while car B moves with a constant velocity v = 1 m/s. At time t = 0, car A is 10 m behind car B. Find the time when car A overtakes car B.
View SolutionTwo objects of masses 100g and 200g are moving along the same line in the same line in the same direction with velocities of 2m/s and 1m/s, respectively. They collide and after the collison, the first object moves at a velocity of 1.67m/s in the same direction. Determine the velocity of the second object.
View Solution
Knowledge Check
Car A and car B start moving simultaneously in the same direction along the line joining them. Car A moves with a constant acceleration a=4m/s2, while car B moves with a constant velocity v=1m/s. At time t=0, car A is 10m behind car B. Find the time when car A overtake car B.
A2.5sB3.5sC−2sDnoneTwo particles A and B are projected simultaneously in the direction shown in the figure with velocities VA=20m/s and VB=10m/s respectively. If they collide in air after 1/2 sec. then
 Athe angle θ is 60∘Bthe distance x is 5√3mCthe angle θ is 30∘DThe distance x is 15√3m
Athe angle θ is 60∘Bthe distance x is 5√3mCthe angle θ is 30∘DThe distance x is 15√3mTwo particles A and B are projected simultaneously in horizontal direction with speed 50m/s and 100m/s respectively . If tAandtB are the time taken by the projectiles to hit the ground by the particles A and B respectively, then
AtA=tBBta>tBCtA<tBDInformation is insufficient to compare tAandtB.
A railway carriage of mass 10gand200g are moving along the same line in the same direction with velocities of 2m/sand1m/s respectively. They collide and after the collison, the first object moves with a velocity of 1.67m/s in the same direction. Determine the velocity of the second object.
View SolutionA particle is moving on a straight line with constant retardation of 1m/s2. Its initial velocity is 10m/s.
View SolutionA particle, initially at rest, starts moving in a straight line with an acceleration a=6t+4m/s2. The distance covered by it in 3 s is
View SolutionTwo particles are projected with speed 4m/s and 3m/s simultaneously from same point as shown in the figure. Then :
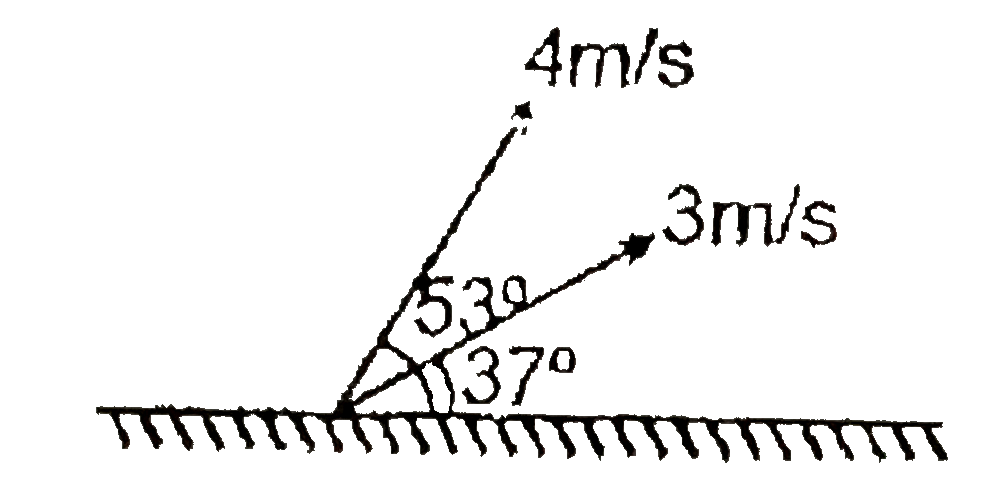
View SolutionTwo particles are projected with speed 4m/s and 3m/s simultaneously from same point as shown in the figure. Then:

View Solution

