A particle moving in a straight line has velocity-displacement equation as Here v is in and s in metres. Select the correct alternative.
Particle is initially at rest
Initially velocity of the particle is and the particle has a constant acceleration of
Particle moves with a uniform velocity
None of the above
The correct Answer is:B
To solve the problem, we need to analyze the given velocity-displacement equation and find the initial velocity and acceleration of the particle.
1. Understanding the Given Equation:
The velocity v of the particle is given by the equation:
v=5√1+s
where v is in meters per second (m/s) and s is in meters (m).
2. Finding the Initial Velocity:
To find the initial velocity, we need to evaluate the velocity when the displacement s is zero:
v=5√1+0=5√1=5m/s
Therefore, the initial velocity v0 is:
v0=5m/s
3. Finding the Acceleration:
Acceleration a can be expressed in terms of velocity and displacement using the formula:
a=vdvds
We need to differentiate v with respect to s.
4. Differentiating Velocity:
First, we differentiate the velocity function:
v=5√1+s
Using the chain rule:
dvds=5⋅12√1+s⋅d(1+s)ds=5⋅12√1+s⋅1=52√1+s
5. Substituting into the Acceleration Formula:
Now, substituting v and dvds into the acceleration formula:
a=v⋅dvds=5√1+s⋅52√1+s=252m/s2
6. Final Results:
The initial velocity is:
v0=5m/s
The acceleration at any time t is:
a=252m/s2
Summary:
- Initial Velocity: 5m/s
- Acceleration: 252m/s2
The velocity v of the particle is given by the equation:
v=5√1+s
where v is in meters per second (m/s) and s is in meters (m).
To find the initial velocity, we need to evaluate the velocity when the displacement s is zero:
v=5√1+0=5√1=5m/s
Therefore, the initial velocity v0 is:
v0=5m/s
Acceleration a can be expressed in terms of velocity and displacement using the formula:
a=vdvds
We need to differentiate v with respect to s.
First, we differentiate the velocity function:
v=5√1+s
Using the chain rule:
dvds=5⋅12√1+s⋅d(1+s)ds=5⋅12√1+s⋅1=52√1+s
Now, substituting v and dvds into the acceleration formula:
a=v⋅dvds=5√1+s⋅52√1+s=252m/s2
The initial velocity is:
v0=5m/s
The acceleration at any time t is:
a=252m/s2
- Initial Velocity: 5m/s
- Acceleration: 252m/s2
Topper's Solved these Questions
- KINEMATICSBook:DC PANDEYChapter:KINEMATICSExercise:Subjective
Explore 51 Videos
- KINEMATICSBook:DC PANDEYChapter:KINEMATICSExercise:More Than One Correct
Explore 6 Videos
- KINEMATICSBook:DC PANDEYChapter:KINEMATICSExercise:Assertion And Reason
Explore 12 Videos
- GRAVITATIONBook:DC PANDEYChapter:GRAVITATIONExercise:(C) Chapter Exercises
Explore 45 Videos
- KINEMATICS 1Book:DC PANDEYChapter:KINEMATICS 1Exercise:INTEGER_TYPE
Explore 15 Videos
Similar Questions
A particle in moving in a straight line such that its velocity is given by v=12t−3t2, where v is in m//s and t is in seconds. If at =0, the particle is at the origin, find the velocity at t=3s.
View SolutionA particle is moving in a straight line and its velocity varies with its displacement as v=√4+4s m/s. Assume s=0 at t=0. find the displacement of the particle in metres at t=1s.
View Solution
Knowledge Check
A particle moving in a straight in a straight line has velocity and displacement equation as
v=4√1+s,
where v is in m/s and s is in m. The initial velocity of the particle is:A4 m/sB16 m/sC2 m/sDzeroA particle is moving in a straight line . Select the correct option (s).
AIf position and velocity are both negative, then particle moves away from the origin .BIf acceleration of the particle is negative , then magnitude of the velocity of particle may increase .CIf acceleration of the particle is positive , than magnitude of velocity of particle may decrease .DIf velocity of the particle remains zero in a time interval, then acceleration is also zero at any instant during the same time interval .A particle moves along a straight line its velocity dipends on time as v=4t−t2. Then for first 5s:
AAverage velcotu is 25/3ms−1BAverage speed is 10ms−1.CAverage velcotu is 5/3ms−1DAcceleration is 4ms−2 at t=o
A particle moving in a straight line has its velocit varying with time according to relation v=t2−6t+8(m/s) where t is in seconds. The CORRECT statement(s) about motion of this particle is/are:-
View SolutionFor a particle moving along a straight line, its velocity 'v' and displacement 's' are related as v2=cs, here c is a constant. If the displacement of the particle at t=0 is zero, its velocity after 2 sec is:
View SolutionDisplacement time graph of a particle moving in a straight line is as shown in figure. Select the correct alternative (s) :
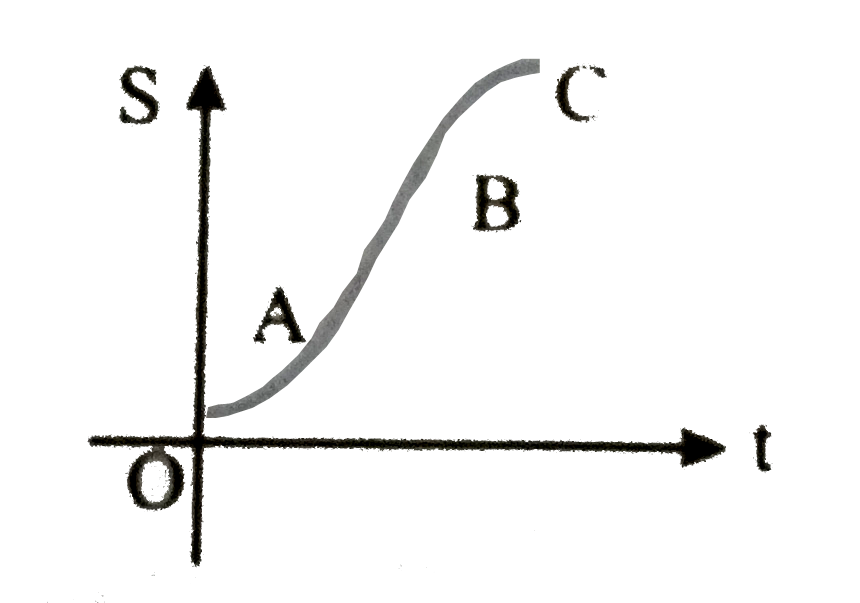 .
.
View SolutionThe speed v of a particle moving along a straight line. When it is at distance x from a fixed point on the line is v2=144−9x2. Select the correct alternatives
View SolutionThe displacement of a particle moving in a straight line is described by the relation s=6+12t−2t2. Here s is in metre and t in second. The distance covered by the particle in first 5s is
View Solution
