चित्र में, BC ।। XY, BX ।। CA तथा AB ।। YC हो, तो सिद्ध कीजिए कि
ar(ΔABX)=ar(ΔACY)
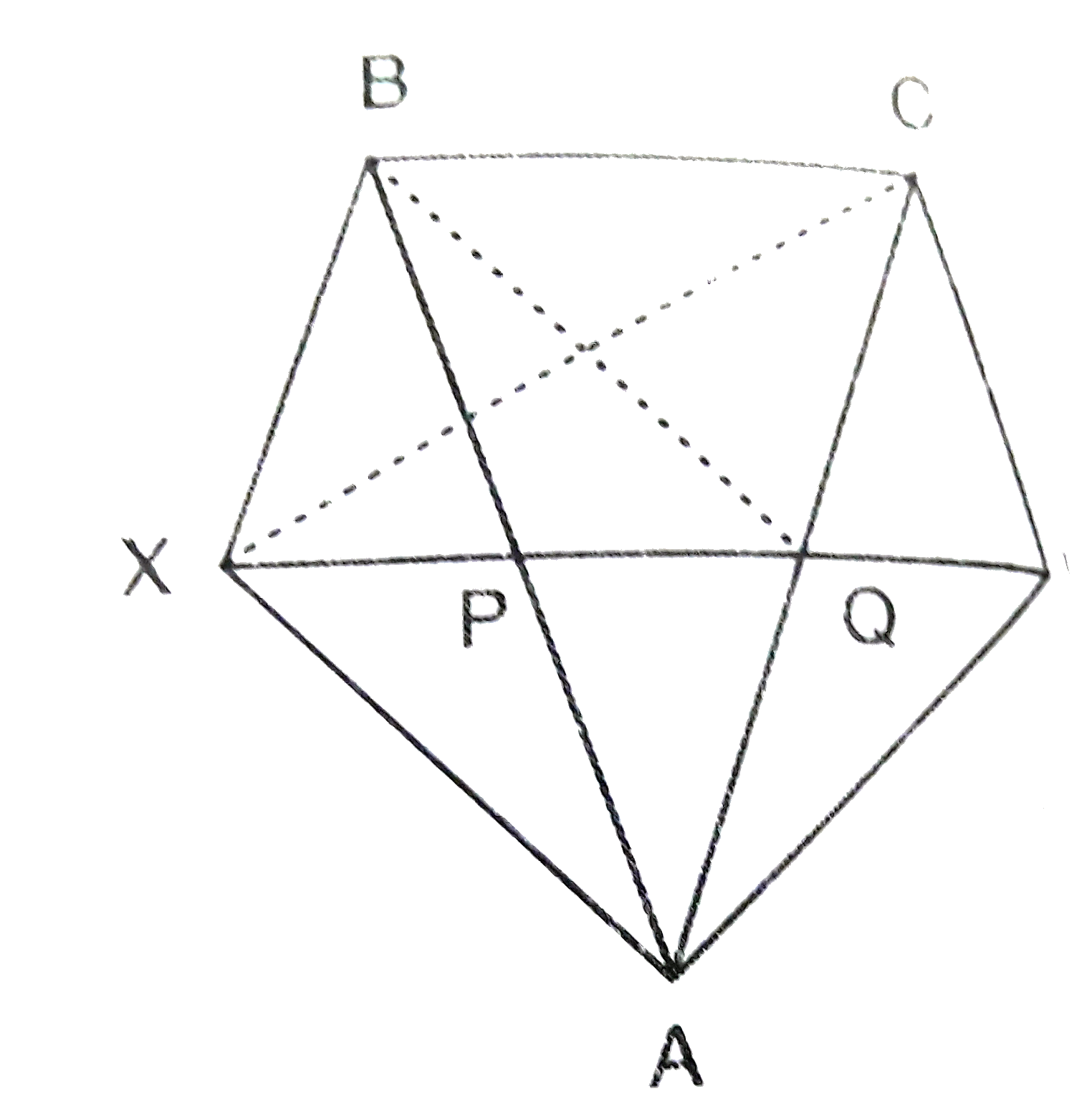
XC तथा BY को मिलाइये ।
चूँकि ΔBXC तथा ΔBCY एक ही आधार BC पर तथा समान समांतर रेखाओं BC तथा XY के बीच स्थित हैं।
∴ar(ΔBXC)=ar(ΔBCY) ...(i)
साथ ही, ΔBXC तथा ΔABX एक ही आधार BX पर तथा समान समांतर रेखाओं BX तथा AC के बीच स्थित हैं।
∴ar(ΔBXC)=ar(ΔABX) ...(ii)
स्पष्तः, ΔBCY तथा ΔACY एक ही आधार CY तथा सामान समांतर रेखाओं AB तथा CY के बीच स्थित हैं ।
∴ar(ΔBCY)=ar(ΔACY) ...(iii)
(i ), (ii ) तथा (iii ) से
ar(ΔABX)=ar(ΔACY)
Topper's Solved these Questions
- समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल BOOK - RD SHARMACHAPTER - समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल EXERCISE - व्याख्यात्मक उदाहरण
1 Videos
- समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल BOOK - RD SHARMACHAPTER - समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल EXERCISE - प्रश्नावली 15.1
6 Videos
- संख्यिकीय आंकड़ों का आलेखीय निरूपण BOOK - RD SHARMACHAPTER - संख्यिकीय आंकड़ों का आलेखीय निरूपण EXERCISE - बहु विकल्पीय प्रश्न
8 Videos
- सर्वांगसम त्रिभुजेंBOOK - RD SHARMACHAPTER - सर्वांगसम त्रिभुजेंEXERCISE - बहु विकल्पीय प्रश्न
17 Videos
Similar Questions
चित्र में , P समान्तर चतुर्भुज ABCD के अभ्यन्तर में स्थित कोई बिंदु है दर्शाइए कि
(i) ar(ΔAPB)+ar(ΔPCD)=12ar(।।gmABCD)
(ii) ar(ΔAPD)+ar(ΔPBC)=ar(ΔAPB)+ar(ΔPCD)

View Solutionआकृति में आकृति एक ही आधार तथा समान समांतर रेखाओं के बीच स्थित है :

View Solutionनिम्न में से कौन - सा , सांख्यिकीय आकड़ो का लेखा चित्रीय निरूपण नहीं है ?
View Solutionयदि ΔABC≅ΔLKMहों, तो ΔLKMकी कौन सी भुजा ΔABCकी भुजा BC के एक बराबर होगी ?
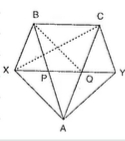
View SolutionIn Figure, BC||XY,BX||CA and AB∣∣YC Prove that: ar(ABX)=ar(ACY)
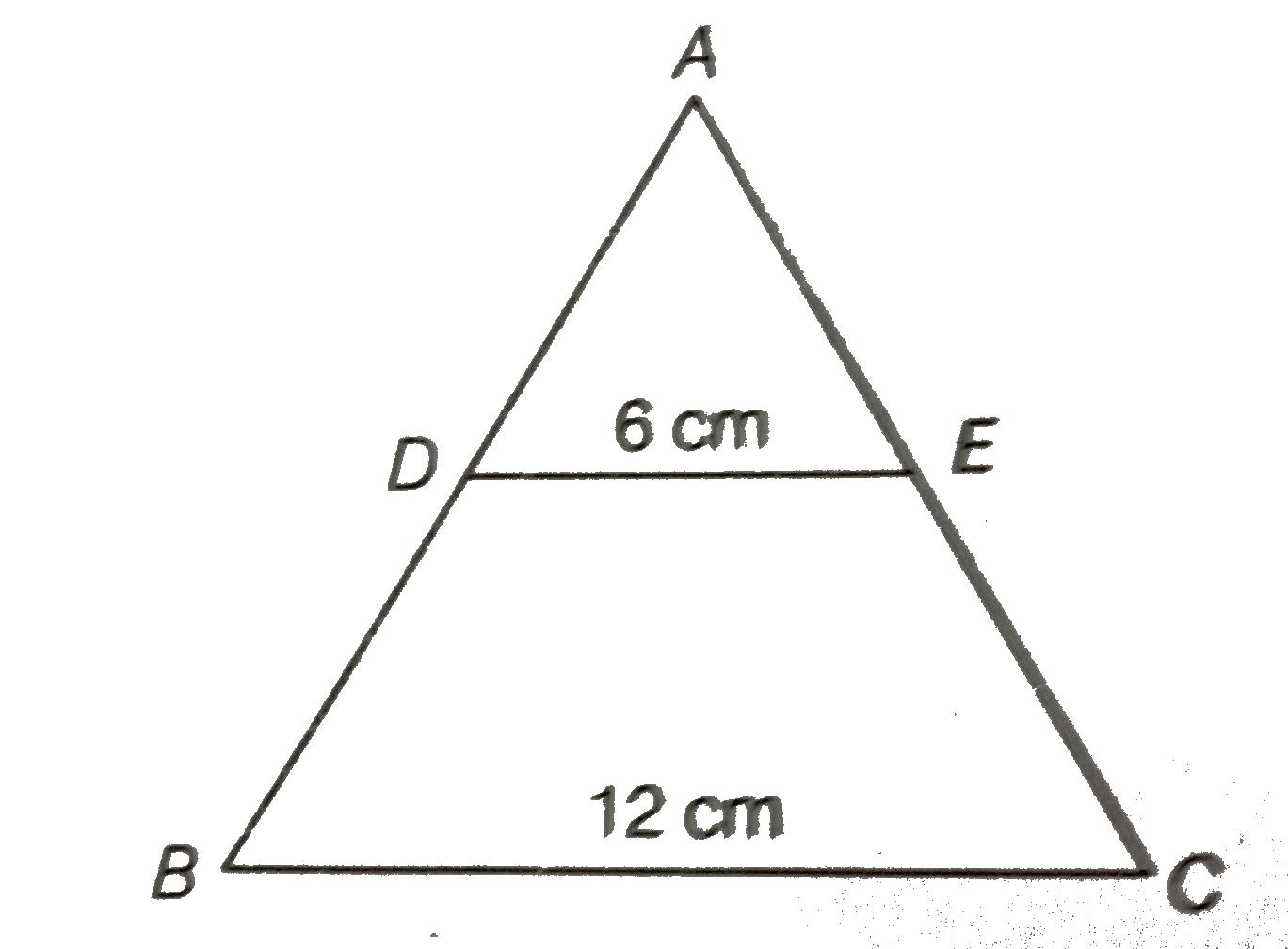
View SolutionIn figure, if DE||BC, then find the ratio of ar (ΔADE) and ar(DECB).
View SolutionIn the given figure, BC||XY,BX||CAandAB∣∣YC. Prove that area (ΔABX)= area (ΔACY)

View SolutionABCD एक समलम्ब है, जिसमें AB ।। DC हैं। AC के समान्तर एक रेखा AB को X तथा BC को Y पर प्रतिच्छेद करती है। सिद्ध करो कि ar(ΔADX)=ar(ΔACY)
View Solutionयदि ΔABC~ΔPQR तथा BC=5QR तो ar(ΔABC):ar(ΔPQR) है
View Solutionचित्र में AB ,BC तथा CA वृत्त कि स्पर्श रेखाएं है। यदि BC=6.3 सेमी तथा MC=2.7 सेमी हो ,तो BL कि नाप लिखिए।

View Solutionकिसी समांतर चतुर्भुज ABCD में यदि −−→AB=¯a तथा −−→BC=¯b तो सिद्ध कीजिए कि
−−→AC=¯a+¯b और −−→BD=¯b−¯a.
View Solutionयदि बिन्दु (a,b),(a',b') और (a−a',b−b') संरेख हो तो सिद्ध कीजिए कि
ab'=a'b.
साथ ही यह भी सिद्ध कीजिए कि इन बिन्दुओं से होकर जाने वाली रेखा मुलबिन्दु से होकर जाती है।
View Solutionयदि समान्तर चतुर्भुज कि दो आसान भुजाएँ →a तथा →b हो , तो इसका विकर्ण ज्ञात कीजिए।
View Solutionयदि ab=cd हो, तो सिद्ध कीजिए कि ab=a+cb+d |
View Solutionयदि x=asinθ तथा y=acosθ हो, तो सिद्ध कीजिए कि x2+y2=a2
View Solution
