चित्र 8 में, एक ही आधार BC पर तथा विपरीत दिशाओं में दो त्रिभुज △ABC तथा △DBC बने हुए हैं तथा AD और BC का प्रतिच्छेदन बिन्दु O है। सिद्ध कीजिए कि क्षेत्रफल (△ABC) क्षेत्रफल (△DBC)=AODO

AL⊥BCतथा DM⊥BC
Δ'sAOLतथा DOM समरूपहै
⇒AODO=ALDM
"अब, "("क्षे"(triangleABC))/("क्षे"(triangleBCD))==((cancel1)/(cancel2)cancel(BC).AL)/(cancel(1)/(cancel2)cancel(BC).DM)=(AO)/(DO) 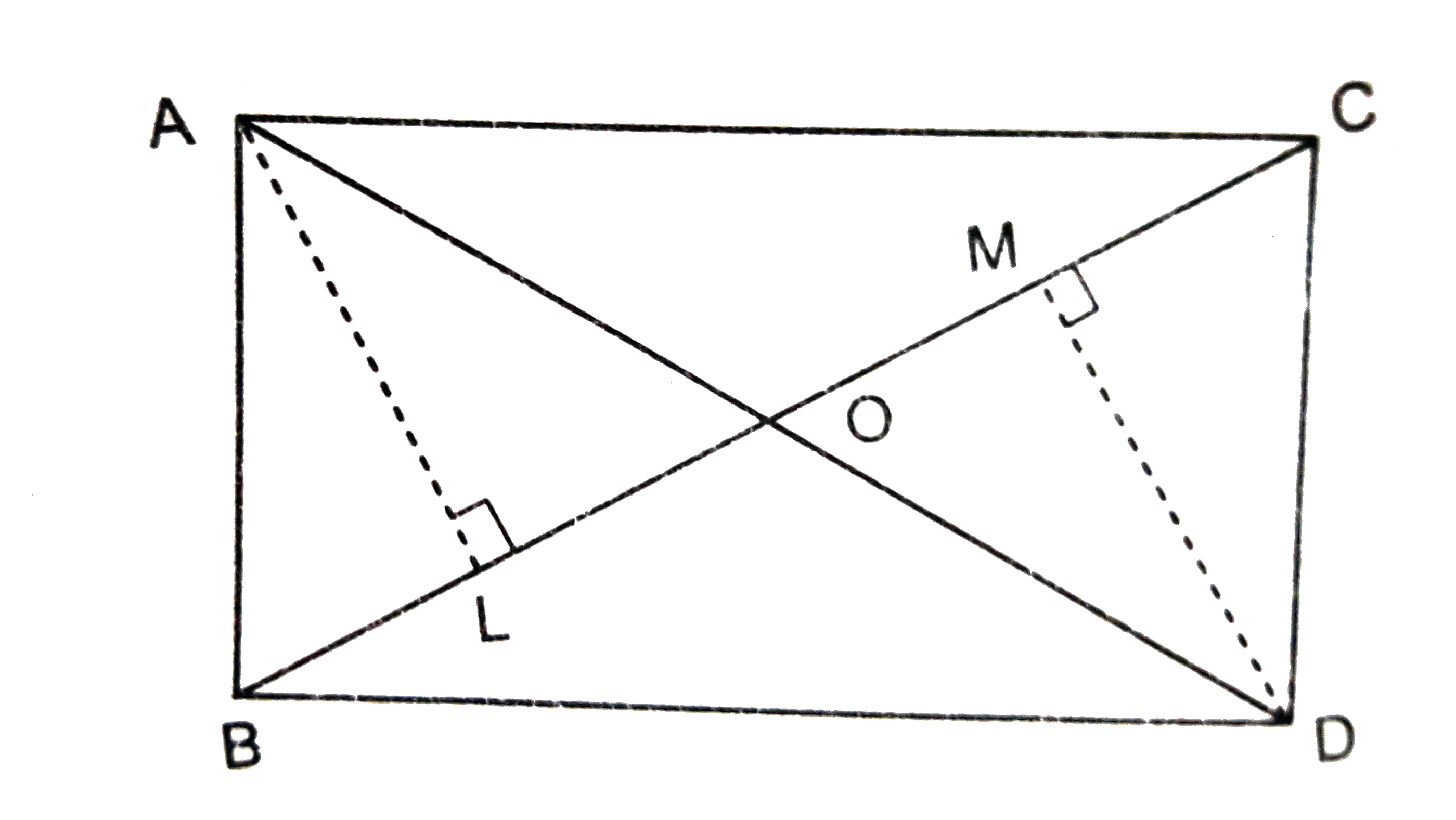
Topper's Solved these Questions
- CCE-SUMMATIVE ASSESSMENT (TERM 1)BOOK - RD SHARMACHAPTER - CCE-SUMMATIVE ASSESSMENT (TERM 1)EXERCISE - सैंपल प्रश्नपत्र - 2
40 Videos
- CCE-SUMMATIVE ASSESSMENT (TERM 1)BOOK - RD SHARMACHAPTER - CCE-SUMMATIVE ASSESSMENT (TERM 1)EXERCISE - सैंपल प्रश्नपत्र - 3
39 Videos
- सांख्यिकीBOOK - RD SHARMACHAPTER - सांख्यिकीEXERCISE - बहु विकल्पीय प्रश्न
35 Videos
- CCE-SUMMATIVE ASSESSMENT (TERM-2) BOOK - RD SHARMACHAPTER - CCE-SUMMATIVE ASSESSMENT (TERM-2) EXERCISE - सैंपल प्रश्नपत्र - 4
31 Videos
Similar Questions
निम्न संख्याओं में से किस संख्या का दशमलव प्रसार सान्त है?
View Solutionपरिमेय संख्या 4324×53 का दशमलव प्रसारण सांत होगा, निम्न दशमलव स्थानों के पश्चात्:
View Solutionनिम्न में कौन सी केन्द्रीय प्रवृत्ति का माप नहीं है ?
View Solutionदो संकेन्द्रीय वृत्त हैं जिनकी त्रिज्याएँ 13 सेमी तथा 5 सेमी है। बड़े वृत्त की उस जीवा की लम्बाई जो छोटे वृत्त को स्पर्श करती है, है:
View Solution△ABCand△DBC are two triangles on the same base BC. A and D lies on opposite sides of BC. Prove that ar(△ABC)ar(△DBC)=AODO
View SolutionDetermine the point of symmetry of a regular hexagon.
View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionThe inequation represented by the graph given below is :
View SolutionThe inequation that best describes the graph given below is _________
View SolutionThe inequation that best describes the following graph is _________
View SolutionIn the adjoining figure, △ABCand△DBC are on the same base BC with A and D on opposite sides of BC such that ar(△ABC)=ar(△DBC). Show that BC bisect AD.
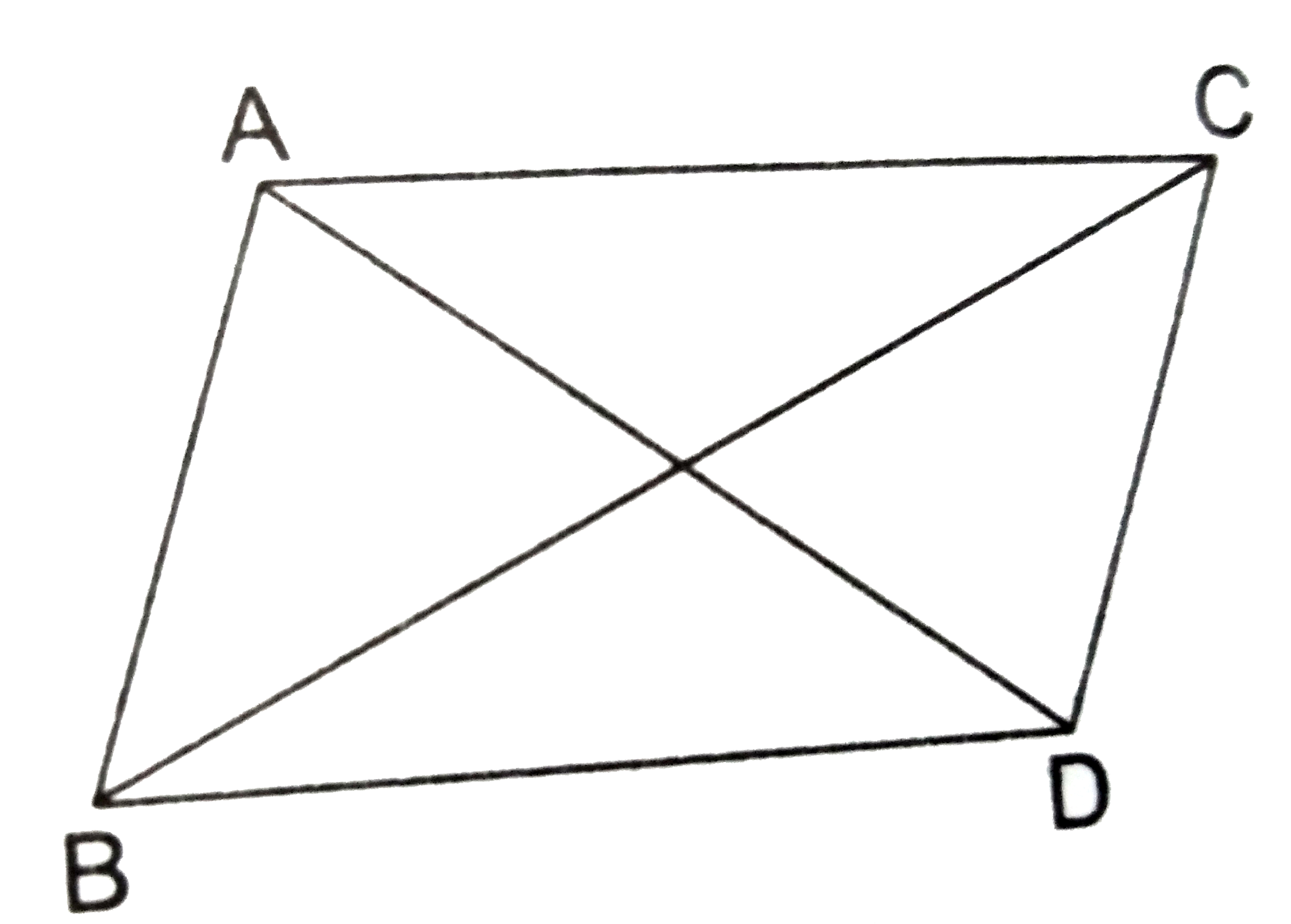
View Solutionएक ही आधार BC पर तीन समद्विबाहु त्रिभुज △PBC ,△QBC और △RBC स्तिथ है। सिद्ध कीजिए कि P ,Q और R समरेख है।
View Solutionएक त्रिभुज का एक शीर्ष (1,2) पर है तथा इससे होकर जाने वाली दो भुजाओं के मध्य - बिन्दु (−1,1) और (2,3) हैं , तो इस त्रिभुज का केन्द्रक है
View Solution
