Define linear simple harmonic motion. Assuming the expression for displacement of a particle starting from extreme position, explain graphically the varition of velocity and acceleration w.r.t. time.
A clock reagulated by seconds pendulum, keeps correct time. During summer, length of pendulum increases to 1.005 m. How much will the clock gain or loose in one day (g=9.8m/s2andπ=3.142).
Linear Simple Harmonic Motion : It is defined as the linear periodic motion of a body, in which the restoring force (or acceleration) is always directed towards the mean position and its magnitude is directly proportional to the displacement from the mean position.
Particle performing S.H.M. starting fromm extreme position :
Equation of displacement is x=acosωt
At extreme position, α=π/2.
∴ Velocity of particle is v=dxdt=ddt(acosωt)
And v=−aωsinωt
acceleration of a particle =dvdt
=ddt=(−aωsinωt)
=−aω2cosωt.
Substiuting ω=2π/T in above equaitons

(i) Displancement, veloctiy and acceleration of S.H.M. are periodic functions of time.
(ii) Displancement-time curve and acceleration-time curve are cosine curve and velocity-time curve is a since curve.
(iii) Phase difference between displacement and velocity is
π2 radian.
(iv) Phase difference between velocity and acceleration is π2 radian.
(v) Phase difference between displacement and acceleration is π radian.
(vi) At extreme position, displancement and acceleration is maximum while velocity is minimum.
(vii) After the phase of 2π radian, all curves repeat the same path.
Given L=1.005m and g =9.8m/s2
Period of simple pendulum (T)
=2π√Lg
T=2×3.142×√1.0059.8
=2.012sec.<br>Now,secondspendu––mhasaperiodof2sec.<br>Therefore,thegivenclockwilll∞se(2.012-2)sec=0.012secdur∈g∑mer.<br>:.Loss∈periodperday(24xx3600xx0.012)/(2.012)<br>=515.3 sec.
Similar Questions
Define linear simple harmonic motion. Assuming the expression for displacement of a particle starting from extreme position, explain graphically the varition of velocity and acceleration w.r.t. time.
A clock reagulated by seconds pendulum, keeps correct time. During summer, length of pendulum increases to 1.005 m. How much will the clock gain or loose in one day (g=9.8m/s2andπ=3.142).
View SolutionA particle is executing simple harmonic motion with an amplitude of 10 cm and time period of 4s. Calculate its displacement, velocity and acceleration after 1/2 seconds, starting from the mean position.
View Solution
Knowledge Check
A simple harmonic motion along the x-axis has the following properties: amplitude =0.4m the time to go from one extreme position to other is 2s and x=0.3m at t=0.5a. the general equation of the simple harmonic motion is
Ax=(0.5m)sin[πt2+8∘]Bx=(0.5m)sin[πt2−8∘]Cx=(0.5m)cos[πt2+8∘]Dx=(0.5m)cos[πt2−8∘]
A particle is executing simple harmonic motion with time period of 4 s and amplitude 10 cm. Calculate displacement, velocity after 12 second starting from mean position.
View SolutionVelocity-time equation of a particle moving in a straight line is, v=(10+2t+3t2) (SI units) Find
(a) displacement of particle from the mean position at time t=1s, if it is given that displacement is 20m at time t=0.
(b) acceleration-time equation.
View SolutionDefine phase of S.H.M. Show variation of displacement, velocity and acceleration with phase for a particle perfoming linear S.H.M. graphically, when it starts from extreme position.
A body starts rotating from rest. Due to a couple of 20Nm it completes 60 revolutions in one minute. Find the moment of inertia of the body.
View SolutionVelocity-time graph of a particle moving in a straight line is shown in figure. At time t=0, displacement of the particle from mean position is 10 m. Find
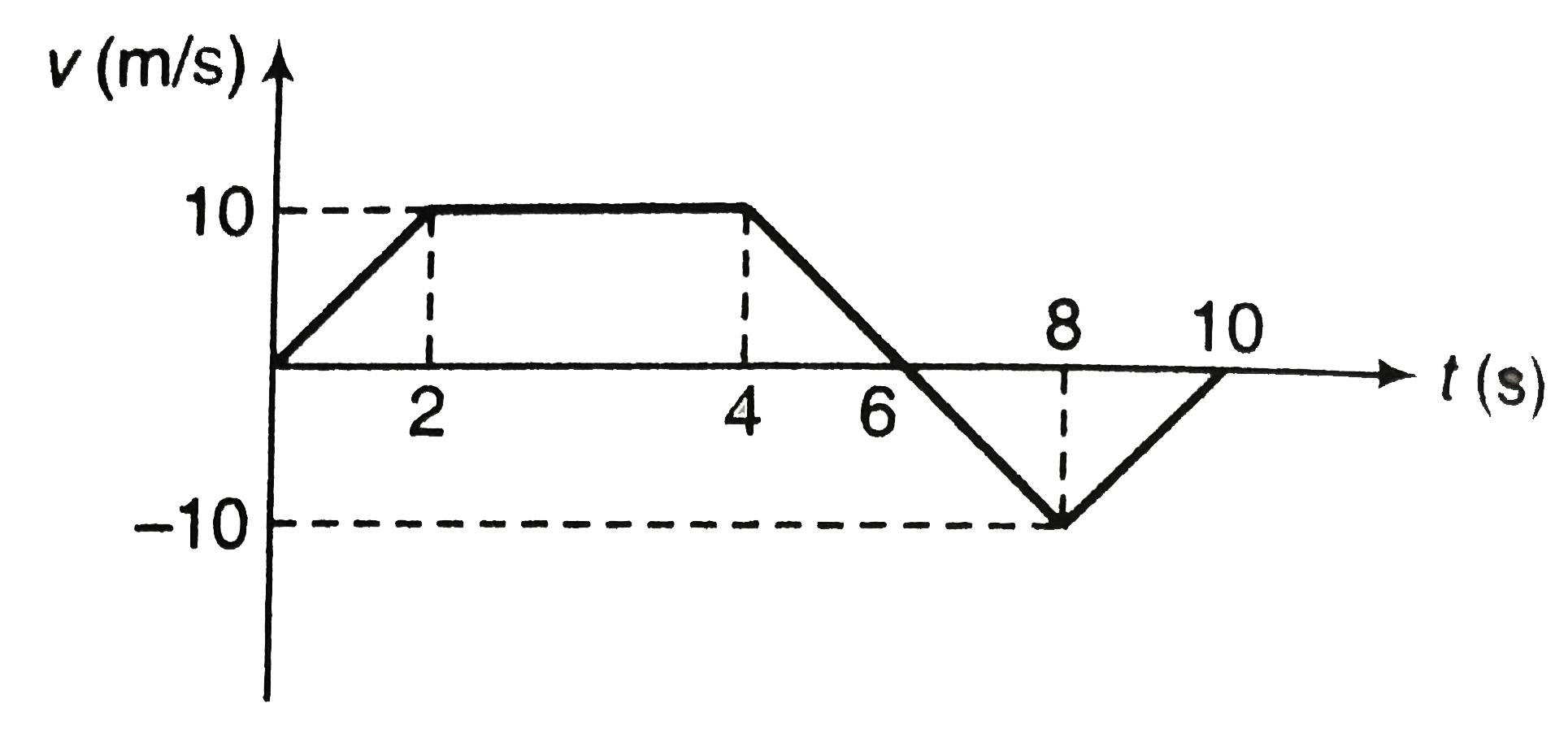
(a) acceleration of particle at t=1s,3sand9s.
(b) position of particle from mean position at t=10s.
(c) write down s-t equation for time interval (i)0≤t≤2s, (ii) 4s≤t≤8s
View SolutionA particle executing simple harmonic motion along a straight line. The velocity of the particle is 5ms−1, when it is at a distance of 4 m from mean position and 3ms−1, when at a distance of 9 m from mean position. Calculate the time taken by the particle to travel 3 m from the positive extremity of oscillation.
View SolutionAs velocity of the particle increases from zero and finally it decreases to zero hence acceleration is not remain positive for all the time of motion. Find out the average velocity of the motion V(m/s) 4 1/2 0 >t(sec) 1
View SolutionA clock with a brass pendulum shaft keeps correct time at a certain temperature.
a. How closely must the temperature be controlled if the clock is not to gain or lose more that 1 s a day? Does the answer depend on the period of the pendulum?
b. Will an increase of temperature cause the clock to gain or lose? (αbrass=2×10−5/∘C)
View Solution

