A thin ring has mass 0.25 kg and radius 0.5 m. Its moment of inertia about an axis passing through its centre and perpendicular to its plane is ………… .
0.0625kgm2
0.625kgm2
6.25kgm2
62.5kgm2
The correct Answer is:A
Step by step video & text solution for A thin ring has mass 0.25 kg and radius 0.5 m. Its moment of inertia about an axis passing through its centre and perpendicular to its plane is ………… . by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- FEBRUARY 2018BOOK - GURUKUL PUBLICATION - MAHARASHTRA PREVIOUS YEAR PAPERSCHAPTER - FEBRUARY 2018EXERCISE - SECTION-II
21 Videos
- FEBRUARY 2016BOOK - GURUKUL PUBLICATION - MAHARASHTRA PREVIOUS YEAR PAPERSCHAPTER - FEBRUARY 2016EXERCISE - SECTION-II
21 Videos
- FEBRUARY 2019BOOK - GURUKUL PUBLICATION - MAHARASHTRA PREVIOUS YEAR PAPERSCHAPTER - FEBRUARY 2019EXERCISE - SECTION-D
6 Videos
Similar Questions
Calculate the moment of inertia of a ring of mass 2 kg and radius 50 cm about an axis passing through its centre and perpendicular to its plane
View SolutionA disc of radius R has a concentric hole of radius R /2 and its mass is M. Its moment of inertia about an axis through its centre and perpendicular to its plane, is
View Solution
Knowledge Check
A uniform disc of mass 5 kg has a radius of 0.5 m. Its moment of inertia about an axis passing through a point on its circumference and perpendicular to its plane is
A1.25 kg - m2B0.5 kg - m2C4 kg - m2D1.875 kg - m2Moment of inertia of a circular ring about an axis through its centre and perpendicular to its plane is
AI=12MR2BI=MR2CI=32MR2DI=52MR2A solid cylinder has mass M radius R and length / its moment of inertia about an axis passing through its centre and perpendicular to its own axis is
A2MR23+MI212BMR23+MI212C3MR23+MI212DMR24+MI212
A square of a side a is cut from a square of side 2a as shown in the figure. Mass of this square with a hole is M. Then its moment of inertia about an axis passing through its centre of mass and perpendicular to its plane will be
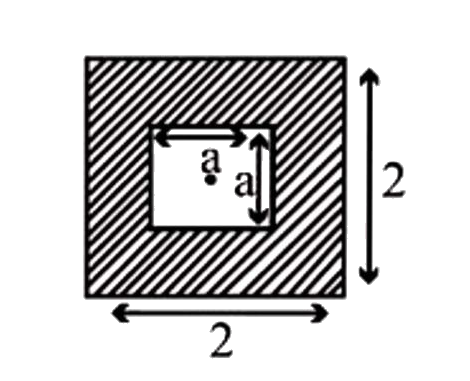
View SolutionThe moment of inertia of a uniform circular disc about a tangent in its own plane is 54MR2 , where M is mass and R is the radius of the disc. Find its moment of inertia about an axis through its centre and perpendicular to its plane.
View SolutionA solid cylinder has mass M radius R and length / its moment of inertia about an axis passing through its centre and perpendicular to its own axis is
View SolutionThe diameter of a thin circular disc of mass 2 kg is 0.2 m. Its moment of inertia about an axis passing through the edge and perpendicular to the plane of the disc is
View SolutionA circular thin disc of mass 2 kg has a diameter 0.2 m. Calculate its moment of inertia about an axis passing through the edge and perpendicular to the plane of the disc (in kg m2)
View Solution
