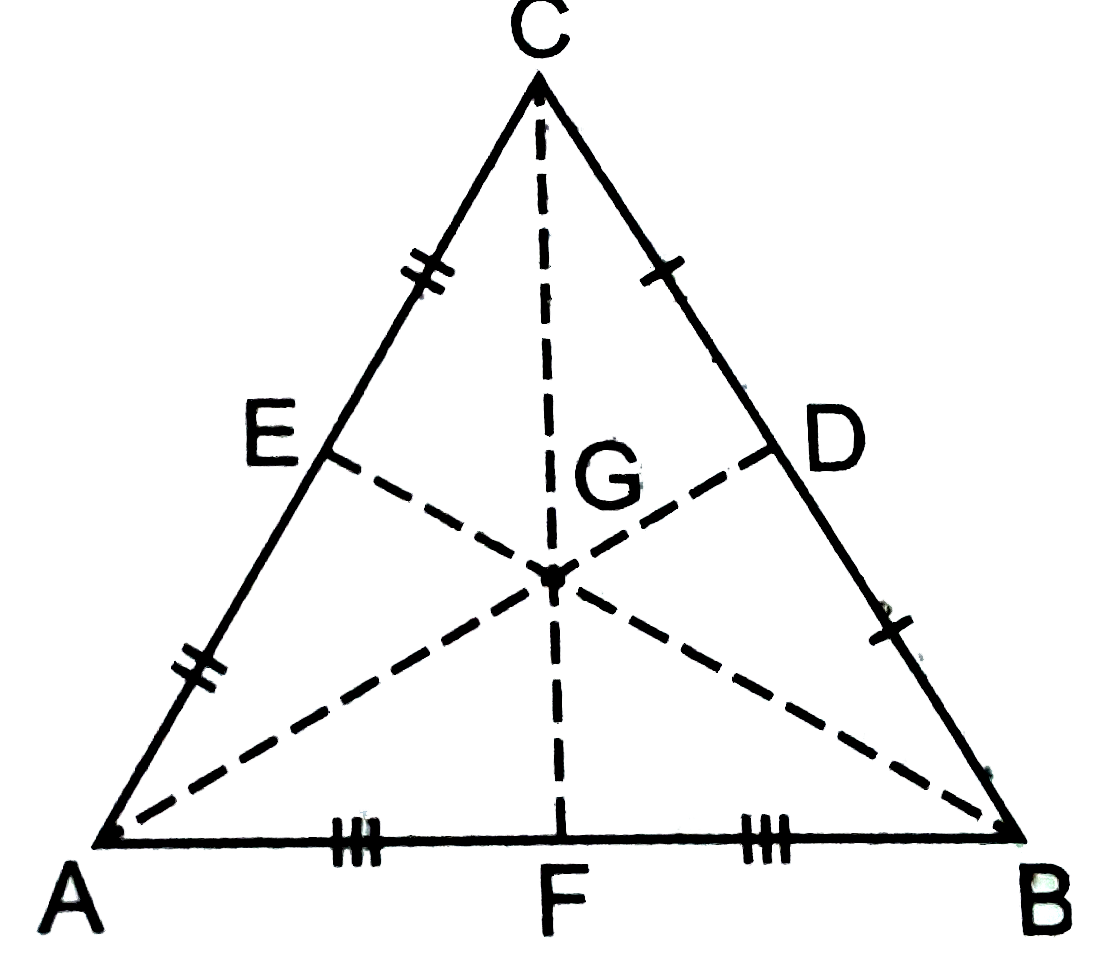
Prove using vectors: Medians of a triangle are concurrent.
Let A, B and C be vertices of a triangle.
Let D, E and F be the midpoints of the sides BC, AC and AB respectively .Let −−→OA=→a,−−→OB=→b,−−→OC=→c,−−→OD=→d,−−→OE=→eand−−→OF=→f be position vectors of points A, B, C, D, E and F respectively.
Therefore , by midpoint formula,
→d=→b+→c2,→e=→a+→c2
and →f=→a+→b2
∴2→d=→b+→c,2→e=→a+→c
and 2→f=→a+→b
∴2→d+→a=→a+→b+→c,
2→e+→b=→a+→b+→c
2→f+→c=→a+→b+→c
Now, 2→d+→a3=2→e+→b3
=2→f+→c3=→a+→b+→c3
Let →g=→a+→b+→c3.
Then , we have →g=→a+→b+→c3
=(2)→d+(1)→a2+1
=(2)→e+(1)→b2+1
=(2)→f+(1)→c2+1
If G is the point whose position vector is →g , then from the above equation it is clear that the point G lies on the medians AD, BE, CF and it divides them internally in the ratio 2:1.
Hence, the medians of a triangle are concurrent .
Topper's Solved these Questions
- MARCH 2018BOOK - GURUKUL PUBLICATION - MAHARASHTRA PREVIOUS YEAR PAPERSCHAPTER - MARCH 2018EXERCISE - SECTION - II
20 Videos
- MARCH 2017BOOK - GURUKUL PUBLICATION - MAHARASHTRA PREVIOUS YEAR PAPERSCHAPTER - MARCH 2017EXERCISE - SECTION-II
20 Videos
- MARCH 2019BOOK - GURUKUL PUBLICATION - MAHARASHTRA PREVIOUS YEAR PAPERSCHAPTER - MARCH 2019EXERCISE - SECTION-D
13 Videos
Similar Questions
Prove using vectors: If two medians of a triangle are equal, then it is isosceles.
View SolutionProve that the internal bisectors of the angles of a triangle are concurrent
View SolutionProve that the internal bisectors of the angles of a triangle are concurrent
View SolutionProve that the medians of a triangle are concurrent and find the position vector of the point of concurrency (that is, the centroid of the triangle)
View SolutionShow that the perpendicular bisectors of the sides of a triangle are concurrent.
View SolutionThe coordinates of points A, B and C are (1,2),(−2,1)and(0,6). Verify if the medians of the triangle ABC are concurrent..
View SolutionProve using vectors: The median to the base of an isosceles triangle is perpendicular to the base.
View SolutionShow, by vector methods, that the angularbisectors of a triangle are concurrent and find an expression for the position vector of the point of concurrency in terms of the position vectors of the vertices.
View SolutionProve that sum of any two medians of a triangle is greater than the third median.
View SolutionProve that any two sides of a triangle are together greater than twice the median drawn to the third side.
View Solution
