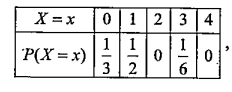
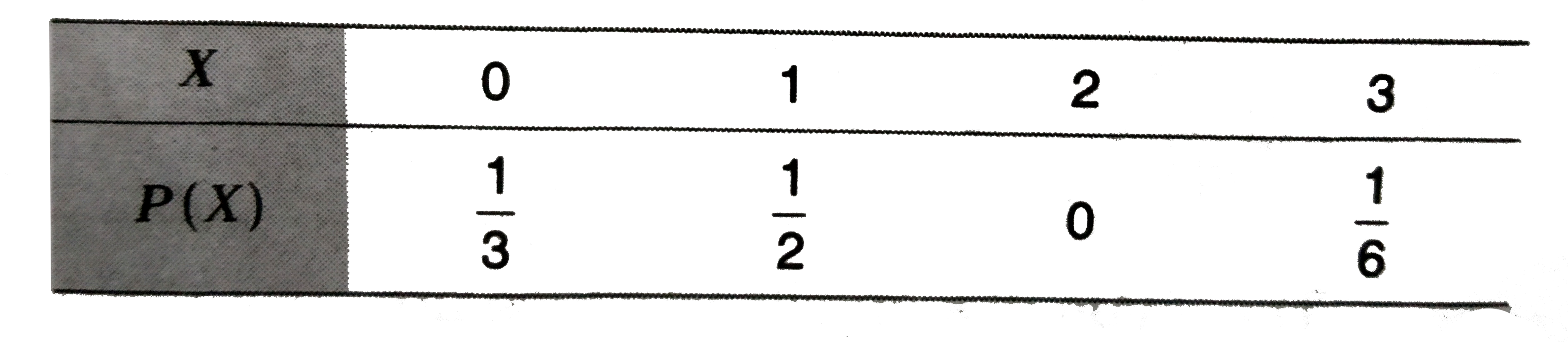
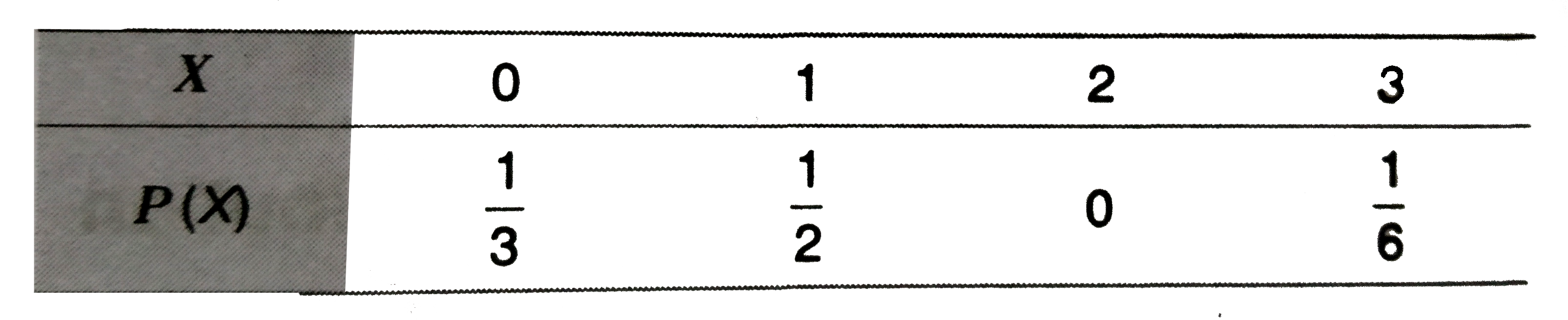
If m and σ2 are the mean and variance of the random variable X whose distribution is given by
A
m=σ2=2
B
m=1,σ2=2
C
m=σ2=1
D
m=2,σ2=1
Video Solution
Text Solution
The correct Answer is:C
Given distribution is
∴ Mean,m=4∑i=1pixi=0×13+1×12+2×0+3×16
=0+12+012=1
Variance , σ2=4∑i=1pi(xi−m)2
=13(0−1)2+12(1−1)2+0(2−1)2+16(3−1)2
=13+0+0+23=1
∴ m=σ2=1
|
Topper's Solved these Questions
- PROBABILITYBook:MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSChapter:PROBABILITYExercise:Exercise 2 (MISCELLANEOUS PROBLEMS)
Explore 40 Videos
- PROBABILITYBook:MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSChapter:PROBABILITYExercise:MHT CET Corner
Explore 4 Videos
- PROBABILITYBook:MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSChapter:PROBABILITYExercise:PRACTICE EXERCISE (Exercies 2 (MISCELLANEOUS PROBLEMS))
Explore 30 Videos
- PRACTICE SET 24Book:MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSChapter:PRACTICE SET 24Exercise:Paper 2 (Mathmatics)
Explore 50 Videos
- SEQUENCES AND SERIES Book:MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSChapter:SEQUENCES AND SERIES Exercise:EXERCISE 31
Explore 1 Video
Similar Questions
Knowledge Check
If the mean and variance of a random variable X having a binomial distribution of 8 terms, are 4 and 2, respectively. Then P(X>6) is equal to
A1256B3256C9256D7256If the mean and variance of a random variable X having a Binomial distribution and 4 and 2 respectively, then find the value of P(X-1).
A1/4B1/16C1/8D1/32The mean and variance of a random variable X having a binomial distribution are 4 and 2 respectively, then P(X=1) is
A132B18C14D116
Find the variance and standard deviation of the random variable X whose probability distribution is given below :
x0123P(X=x)18383818
View SolutionMean of a discrete random variable
View SolutionThe mean and variance of the random variable X which follows the following distribution are respectively.
X = x:- 1 2 3 4
p( X = x):- 0.1 0.2 0.3 0.4
View SolutionFind the mean and variance of the frequency distribution given below

View SolutionA random variable X has the probability distribution given below
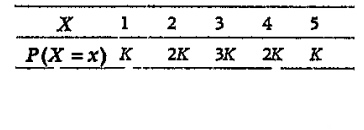
Its variance is
View Solution