In a dice game , a player pays a stake of ₹1 for each throw of a die. She receives ₹5, if the die shows a 3, ₹ 2, if the die shows a 1 or 6 and nothing otherwise, then what is the player's expected profit per throw over a long series of throws?
0.5
0.2
0.7
0.9
The correct Answer is:A
Let X be the money won in one throw
Money lost in 1 throw = र1
Also, probability of getting 3=16
probability of getting 1 or 6
⇒ 16+16=26
probability of getting any other number i.e. 2 or 4 or 5
=16+16+16=36
Then probability distribution is
The expected money that player can won
E(X)=56+46+0=96=र1.5
Then, players expected profit =र 1.5-र 1=र 0.50

Topper's Solved these Questions
- PROBABILITYBook:MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSChapter:PROBABILITYExercise:Exercise 2 (MISCELLANEOUS PROBLEMS)
Explore 40 Videos
- PROBABILITYBook:MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSChapter:PROBABILITYExercise:MHT CET Corner
Explore 4 Videos
- PROBABILITYBook:MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSChapter:PROBABILITYExercise:PRACTICE EXERCISE (Exercies 2 (MISCELLANEOUS PROBLEMS))
Explore 30 Videos
- PRACTICE SET 24Book:MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSChapter:PRACTICE SET 24Exercise:Paper 2 (Mathmatics)
Explore 50 Videos
- SEQUENCES AND SERIES Book:MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSChapter:SEQUENCES AND SERIES Exercise:EXERCISE 31
Explore 1 Video
Similar Questions
In 60 throws of a die, the outcomes were noted as below:
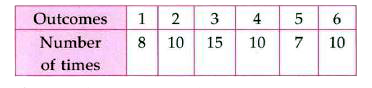
If die is thrown at random, then what is the probability that upper face of a die shows an even prime number?
View SolutionA dice is thrown twice. The probability of getting 4, 5 or 6 in the first throw and 1, 2,3 or 4 in the second throw is
View Solution
Knowledge Check
In a dice game, a player pays a stake of ₹1 for each throw of a die. She receives ₹5, If the die shows a 3,₹2, If the die shows a 1 or 6 and nothing otherwise. What is the player's expected profit per throw over a long series of throws ?
A0.50B0.20C0.70D0.90In a throw of three dice, the probability that at least one die sows up 1, is
A56B91216C136D125216Three dice, each numbered 1 to 6 are rolled. One die is fair and others are biased so that for each of them a six is twice as likely to occur as any other score. One of the dice is chosen at random and on two throws it shows a six on each occasion. The probability that the die chosen was biased is
A423674B288337C118337D323674
A and B throw with one die for a stake of ₨11 which is to be won by the player who first throw 6. If A has the first throw, then what are their respective expectations?
View SolutionIn a game, a man wins Rs 100 if he gets 5 or 6 on a throw of a fair die and loses Rs 50 for getting any other number on the die. If he decides to throw the die either till he gets a five or a six or to a maximum of three throws, then his expected gain/loss (in rupees) is:
(a) 4003 gain
(b) 4009 loss
(c) 0
(d) 4003 loss
View SolutionLet two fair six-faced dice A and B be thrown simultaneously. If E1 is the event that die A shows up four, E2 is the event that die B shows up two and E3 is the event that the sum of numbers on both dice is odd, then which of the following statements is NOT true ? (1) E1 and E2 are independent. (2) E2 and E3 are independent. (3) E1 and E3 are independent. (4) E1 , E2 and E3 are independent.
View SolutionIn two dice game, the player take turns to roll both dice, they can roll as many times as they want in one turn. A player scores the sum of the two dice thrown and gradually reaches a higher score as they continue to roll. If a single number 1 is thrown on either die, the score for that whole turn is lost. Two dice are thrown simultaneously.

What is the probability of getting the sum of atleast 10?
View SolutionIn two dice game, the player take turns to roll both dice, they can roll as many times as they want in one turn. A player scores the sum of the two dice thrown and gradually reaches a higher score as they continue to roll. If a single number 1 is thrown on either die, the score for that whole turn is lost. Two dice are thrown simultaneously.

What is the probability of getting a product of numbers greater than 16?
View Solution

