Show that the area' bounded by the curve y=cex(c>0), the x-axis and two ordinates is proportional to the difference between the ordinates.
A
f(p)f(q)
B
|f(p)−f(q)|
C
f(p)+f(q)
D
√f(p)f(q)
Video Solution
Text Solution
The correct Answer is:B
Required area
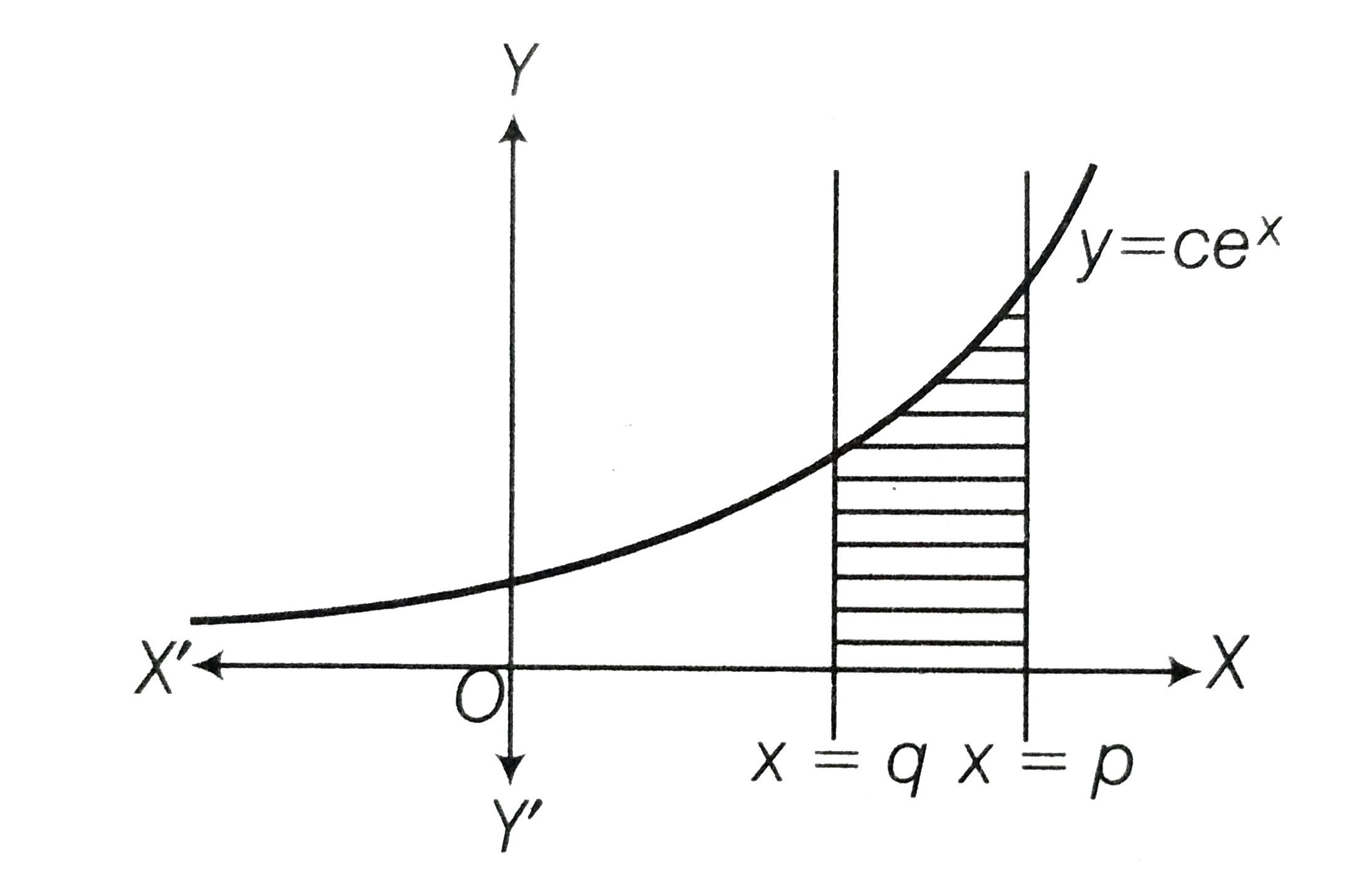
=∣∣∣∫pqcexdx∣∣∣=∣∣[cex]pq∣∣=C|[ep−eq]|
Hence, area is proprtional to |f(p)−f(q)|
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
Area bounded by the curve y=x3, the x-axis and the ordinates x=−2andx=1 is
A-9B−154C154D174Area bounded by the curve y=x2, the x-axis and the ordinates x=−2andx=1 is :
A−9B−154C154D174The area bounded by the curve y=x|x|, x-axis and the ordinates x=1,x=-1 is given by
A0B1/3C2/3D1
Find the area bounded by the curve y=4x−x2, the x-axis and the ordinates x=1 and x=3.
View SolutionThe area bounded by the curve y=4x2 ,x-axis and the ordinates x=1,x=3 is
View SolutionFind the area bounded by the line y=x, the x-axis and the ordinates x=−1 and x=2
View SolutionThe area bounded by the curve f(x)=cex(c>0) ,the x -axis and the two ordinates x=p and x=q is equals to
View SolutionThe area bounded by the curve y = log x, X- axis and the ordinates x = 1, x = 2 is
View Solution
