A vertex of common graph of inequalities 2x+y≥2 and x−y≤3 , is
A
(0,0)
B
(53,−43)
C
(53,43)
D
(−43,53)
Video Solution
Text Solution
The correct Answer is:B
To find a common vertex of inequalities 2x+y≥2andx−y≤3, solve the following equations
2x+y=2.......(i)
and x−y=3...(ii)
On solving Eqs. (i) and (ii) , we get
x=53andy=−43 .
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
The vertex of common graph of inequalities 2x+y≥2andx−y≤3 , is
A(0,0)B(53,−43)C(53,43)D(−43,53)The graph of inequality 3x+y≤3 is:
Aclosed half plane that contains the origin.Bopen half plane that contains the origin.Copen half plane not containing the origin.Dclosed half plane not containing the origin.The solution set of the inequalities 2x+y≥4,x+y≤x,2x−3y≤6 is
A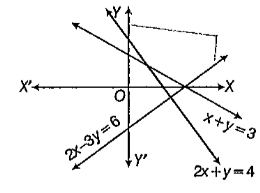 B
B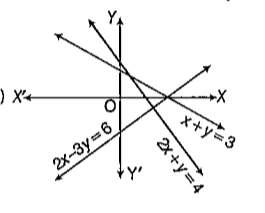 C
C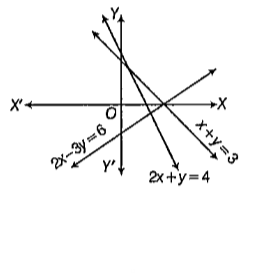 D
D
Draw the graph of the solution set of the inequation 2x+y≥2,x−y≤1,x+2y≤8,x≥0andy≥0
View SolutionConstruct the region represented by the inequations 2x+y≤2andx−3y≤3
View SolutionSolve the following system of linear inequalities
3x+2y≥24,3x+y≤15,x≥4.
View SolutionThe graphical solution of linear inequalities x+y≥5 and x−y≤3,
View SolutionThe solution of the system of inequalities x≥0,y≥0,5x+2y≥10,6x+5y≤30 is a polygonal region with the vertices _________
View Solution
