A uniform ring of mass m and radius a is placed directly above a uniform sphere of mass M and of equal radius. The centre of the ring is at a distance √3a from the centre of the sphere. Find the gravitational force exerted by the sphere on the ring.
dF = force on a small mass dm of the ring by the sphere.
Related Solutions
A uniform ring of mass and radius is placed directly above a uniform sphere of mass and of equal radius. The centre of the ring is at distance from the centre of the sphere. Find the gravitational force exerted by the sphere on the ring.
View SolutionA uniform ring of mas m and radius a is placed directly above a uniform sphere of mass M and of equal radius. The centre of the ring is at a distance a from the centre of the sphere. Find the gravitational force exerted by the sphere on the ring.
View SolutionA uniform ring of mas m and radius a is placed directly above a uniform sphere of mass M and of equal radius. The center of the ring is at a distance from the center of the sphere. Find the gravitational force exerted by the sphere on the ring.
View SolutionA uniform ring of mas m and radius a is placed directly above a uniform sphere of mass M and of equal radius. The center of the ring is at a distance from the center of the sphere. Find the gravitational force exerted by the sphere on the ring.
View SolutionA uniform rig of mas m and radius a is placed directly above a uniform sphre of mass M and of equyal radius. The centre of the ring is at a distance a from the centre of the sphere. Find the gravitational foerce exerted by the sphere on the ring.
View SolutionA uniform ring of mass 2m and radius a is placed directly above the uniform sphere of mass M and of same radius. The centre of ring is at distance sqrt3a from the centre of sphere. The gravitational force exerted by the sphere on the ring is N(GMm)/a^2 units. Calculate is the value of N?
View SolutionA uniform ring of mass m is lying at a distance 1.73 a from the centre of a sphere of mass M just over the sphere where a is the small radius of the ring as well as that of the sphere. Then gravitational force exerted on the sphere is
View SolutionA uniform ring of mass m is lying at a distance 1.73 a from the centre of a sphere of mass M just over the sphere where a is the small radius of the ring as well as that of the sphere. Then gravitational force exerted on the sphere is
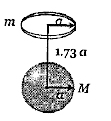
View SolutionA uniform ring of mass M and radius R is placed directly above a uniform sphere of mass 8 m and same radius R. The centre of ring is at a distance of d= sqrt(3)R from the centre of sphere. The gravitational attraction between the sphere and ring is
View SolutionA uniform ring of mass m and radius 3a is kept above a sphere of mass M and radius 3a at a distance of 4a (as shown in figure) such that line joining the centres of ring and sphere is perpendicular to the plane of the ring. Find the force of gravitational attraction between the ring and the sphere.
View SolutionA uniform ring of mass m and radius 3a is kept above a sphere of mass M and radius 3a at a distance of 4a (as shown in figure) such that line joining the centres of ring and sphere is perpendicular to the plane of the ring. Find the force of gravitational attraction between the ring and the sphere.
View SolutionA uiform ring of mass M and radius R is placed directly above a uniform sphere of mass 8M and same radius R. The centre of the sphere. The gravitational atraction between the sphere and the ring is
View SolutionA uniform ring of mass M and radius R is placed directly above a uniform sphere of mass 8M and of same radius R. The centre of the ring is at a distance of from the centre of the sphere. The gravitational attraction between the sphere and the ring is
View SolutionA uniform ring of mass m is lying at a distance sqrt(3) a from the centre of mass M just over the sphere (where a is the radius of the ring as well as that of the sphere). Find the magnitude of gravitational force between them .
View SolutionA uniform ring of mass m is lying at a distance sqrt(3) a from the centre of mass M just over the sphere (where a is the radius of the ring as well as that of the sphere). Find the magnitude of gravitational force between them .
View Solutionद्रव्यमान m एवं त्रिज्या a का एक समरूप वलय M द्रव्यमान के एक समरूप समान त्रिज्या के गोले के ऊपर रखा जाता है। वलय का केंद्र गोले के केंद्र से दूरी पर है। वलय का तल केंद्रो को मिलाने वाली रेखा के ल्रबवत है। वलय पर गोले द्वारा लगाया गया गुरूत्वाकर्षण बल ज्ञात करें।
View SolutionAn unchanged conducting sphere of radius R is placed near a uniformly charge ring of radius R. Total charge on ring is Q. The centre of sphere lies on axis of ring and distance of centre of sphere from centre of ring is R
View SolutionAn unchanged conducting sphere of radius R is placed near a uniformly charge ring of radius R. Total charge on ring is Q. The centre of sphere lies on axis of ring and distance of centre of sphere from centre of ring is R
View Solutionएकसमान वलय जिसका द्रव्यमान M तथा त्रिज्या R है, 8M द्रव्यमान व R त्रिज्या वाले गोले के ऊपर रखी है। वलय का केन्द्र, गोले के केन्द्र से दूरी पर है। वलय तथा गोले के बीच गुरुत्वीय आकर्षण है
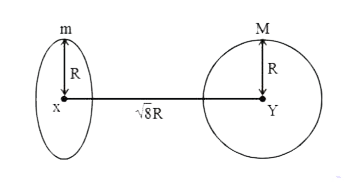
View SolutionFind the gravitational force of attraction between the ring and sphere as shown in the diagram, where the plane of the ring is perpendicular to the line joining the centres. If is the distance between the centres of a ring (of mass 'm') and a sphere (mass "M") where both have equal radius "R'
View Solution