Light with wavelength 530 nm falls on a transparent diffraction grating with period 1.50 μm. Find the angle relative to the grating normal at which the Fraunhofer maximum of highest order is observed provided the light falls on the grating a at right angles; b at the angle 60° to the normal.
a Here the simple formula
Related Solutions
Light with wavelength 530nm falls on a transparent diffraction grating with period 1.50 mu m . Find the angle, relative to the grating normal. At which the Fraunhofer maximum of highest order is observed provided the light falls on the grating (a) at right angles, (b) at the angle 60^(@) to the normal.
View SolutionLight with wavelength lambda falls on a diffracting grating at right angles. Find the angular dispersion of the grating as a function of diffraction angle theta .
View SolutionA transparent diffraction grating has a period . Find the angular disperison (in angular minutes per nanometers) corresponding to the maximum of highest order for a spectral line of wavelength of light falling on the grating
(a) at right angles,
(b) at the angle to the normal.
View SolutionLight with wavelength falls normally on a diffraction grating. Find its period if the diffraction angle corresponds to one of the Fraunhofer maxima and the highest order of spectrum is equal to five.
View SolutionA diffraction grating is ruled with 600 lines per millimetre. When monochromatic light falls normally on the grating, the first order diffracted beams are observed on the far side of the grating each making an angle of 15^@ with the normal to the grating. What is the frequency of the light?
View SolutionDemonstrate that when light falls on a diffracting grating at right angles, the maximum resolving power of the grating cannot exceed the value l//lambda , where l is the width of the grating and lambda is the wavelength of light.
View SolutionA plane wave falls on a diffraction grating with a grating constant at a glancing angle . Prove that the resulting diffraction will be the same as when the wave falls normally on a grating with a grating constant of d = .
View SolutionFind the wavelength of monochromatic light falling normally on a diffraction grating with period if the angle between the directions to the Fraunhofer maxima of the first and the second order is equal to .
View SolutionA monochromatic beam falls on a reflection grating with period at a glancing angle . When it is diffracted at a glancing angle a Fraunhofer maximum of second order occurs. Find the wavelength of light.
View SolutionLight of wavelength 520 nm is falling normally on a plane diffraction grating having 5000 lines per cm. The maximum number of orders of diffracted images seen is :
View SolutionLight of 530 nm wavelenght falls on a grating with a grating constant of 1.50 m. and with a total length of 12.0 mm. Find the angular width of a principal maximum and the resolving power of the grating.
View SolutionWith light falling normally on a diffraction grating, the angle of diffraction of second order is equal to for a wavelength . Find the angle of diffraction of third order for a wave length .
View SolutionA plane light wave with wavelength falls normally on a phase diffraction grating whose side view is shown in Fig. The grating is cut on a glass plate with refractive index . Find the depth of the lines at which the intensity of the central Fraunhofer maximum is equal to zero. what is in this case the diffraction angle corresponding to the first maximum?
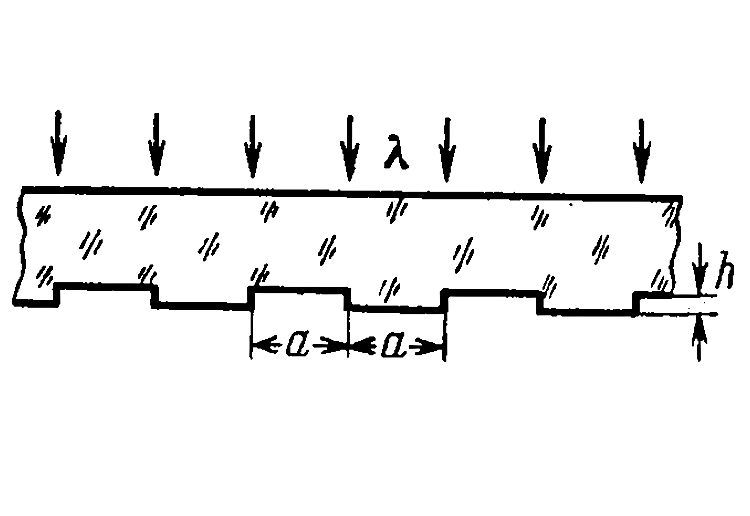
View SolutionFind the wavelenght of monochromatic light falling normally on a diffraction grating with a grating constant of 2.20 mu m15.0^(@).
View SolutionSodium light of wavelength 5890 Å is incident normally on a diffraction grating of 5000 rulings per cm. Find the angle of diffraction for the second order.
View SolutionA beam of monochromatic light of wavelength falls normally on a diffraction grating of line spacing d. If is the angle between the second-order diffracted beam and the direction of the incident light, what is the value of ?
View SolutionA beam of monochromatic light of wavelength falls normally on a diffraction grating of line spacing d. If is the angle between the second-order diffracted beam and the direction of the incident light, what is the value of ?
View SolutionA beam of monochromatic light of wavelength falls normally on a diffraction grating of line spacing d. If is the angle between the second-order diffracted beam and the direction of the incident light, what is the value of ?
View SolutionLight with wavelength lambda = 589.0nm falls normally on a diffraction grating with period d = 2.5mu m , comprising N = 10 000 lines. Find the angular width of the diffraction maximum of second order.
View SolutionLight composed of two spectral lines with wavelength 600.00 and 600.050nm falls normally on a diffraction grating 10.0mm wide. At a centain diffraction angle theta these lines are close to being resolved (according to Rayleigh's criterion). Find theta .
View Solution