A plane monochromatic light wave falls normally on an opaque screen shaped as a long strip with a round hole in the middle. For the observation point P the hole corresponds to half the Fresnel zone with the hole diameter being η = 1.07 times less than the width of the strip. Using Fig. 5.19 find the intensity of light at the point P provided that the intensity of the incident light is equal to I0.
The radius of the first half Fresnel zone is and the amplitude at P is obtained .
Related Solutions
A plane monochromatic light wave falls normally on an opaque screen shaped as a long strip with a round hole in the middle. For the observation point P the hole corresponds to half the Fresnel zone, with the hole diameter being eta = 1.07 times less then the width of the strip. Using Fig. find the intensity of light at the point P provided that the intensity of the incident light is equal to I_(0) .
View SolutionA plane monochromatic wave of natural light with intensity falls normally on an opaque screen with round hole corresponding to the first Fresnel zone for the observation point . Find the intensity of light at the point after the hole was converd with two identical Polaroids whose principle directions are mutually perpendicular and the boundary beween them passes
(a) along the diameter of the hole,
(b) along the circumference of the circle limiting the first half of the fresnel zone.
View SolutionA plane monochromatic light wave with intensity falls normally on an opaque screen with a round aperture. What is the intensity of light behind the screen at the point for which the aperture
(a) is equal to the first Fresnel zone, to the internal half of the first zone,
(b) was made equal to the first Fresnel zone and then half of it was closed (along the diameter) ?
View SolutionA plane monochromatic light wave of intensity I_(0) falls normally on the surfaces of the opaque screens which are shaped as shown in the figure here. The shaped as shown in the gigure here. The rounded-off edge coinicides with the boundary of the first Fresnel zone. Find the intensity of the screens at a point located behind the point P.
View SolutionPlane monochromatic light with intensity I_(0) falls normally on an opaque disc closing the first Fresnel zone for a point on the screen in front of the wave front. What would be the intensity I at the same point if (a) half of the disc along the diameter were removed, (b) half of the external half is removed along the the diameter ?
View SolutionA plane light wave with wavelength lambda and intensity I_(0) falls normally on a large glass plate whose opposite side serves as an opaque screen with a round aperture equal to the first Fresnel zone for the observation point P . In the middle of the aperture there is a round recess equal to half the Fresnel zone. What must the depth h of that recess be for the intensity of light at the point P to be the highest? What is this intensity equal to?
View SolutionA plane monochromatic light wave of intensity I_(0) falls normally on an opaque screen with a long slit having a semicircular cut on one side (Fig.) The edge of the cut coincides with the boundary line of the first Fresnel zone for the observation point P . Thw width of the slit measure 0.90 of the radius of the cut. using Fig. find the intensity of light at the point P .
View SolutionA plane monochromatic light wave with intensity falls normally on an opaque disc closing the first Fresnel zone for the observation point . What did the intensity of light at the point become equal to after
(a) half of the disc (along the diameter) was removed,
(b) half of the external half of the first Fresnal zone removed (along the diameter)?
View SolutionA plane light wave wityh wavelength falls normally on a long opaque strip wide. Behind it a screen is placed at a distance . Using Fig. find the ratio of intensities of light in the middle of the diffraction pattern and at the edge of the geometrical shadow.
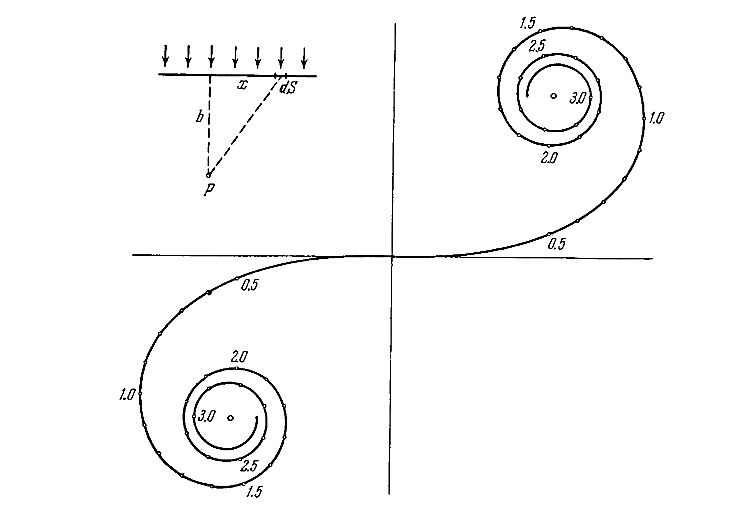
View SolutionA plane monochromatic light wave falls normally on an opaque screen with a long slit whose shape is shown in Fig. Making use of Fig. find the ratio of intensities of light at points and located behind the screen at equal distances from it. For point the rounded-off edge of the slit coincides with the boundary line of the first Fresnel zone.
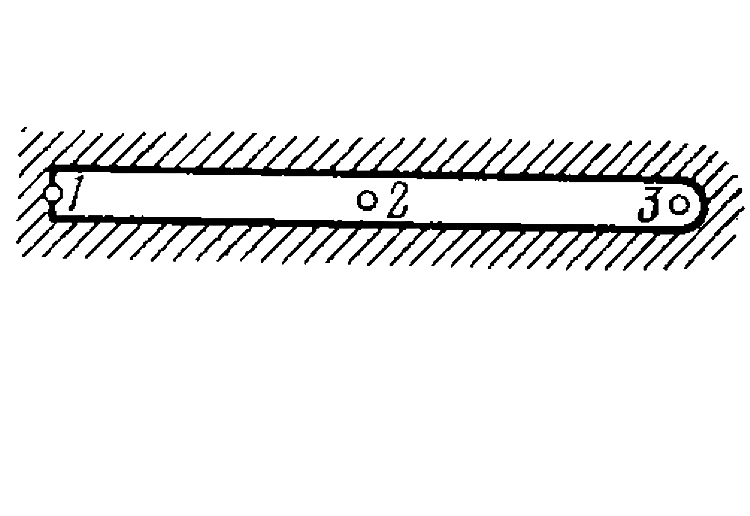
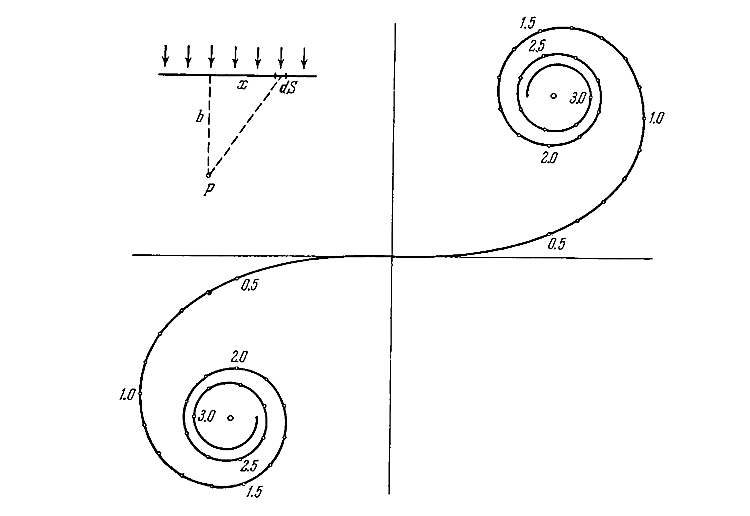
View SolutionA plane monochromatic light wave falls normally on an opaque half-plane. A screen is located at a distance b = 100 cm behind the half-plane. Making use of the cornu spiral (Fig.) find : (a) the ratio of intensities of the first maximum and the neighbouring minimum, (b) the wavelength of light if the first two maxima are separated by a distance Deltax = 0.63mm .
View SolutionA plane monochromatic light wave with intensity falls normally on the surfaces of the opaque screens shown in Fig. Find the intensity of light at a point

(a) located behind the corner ponts of screens and behind the edge of half-plane ,
(b) for which the rounded-off edge of screens coincides with the boundary of the first formula describing the result obtained for screens , the same, for screens .
View SolutionA plane light wave with wavelength lambda = 0.60 mu m falls normally on a sufficiently large glass plate having a round recess on the oppiste side (Fig.) For the observation point P that recess correcponds to the first one and and a half Fresnel zones. Find the depth h of the recess at which the intensity of light at the point P is (a) maximum, (b) minimum, (c ) equal to the intensity of incident light.
View SolutionA plane light wave falls normally on a diaphragm with round aperature opening the first N Fresnel zones for a point P on a screen located at a distance b form the diaphragm. The wavelength of light is equal to lambda . Find the intensity of light I_(0) in front of the diaphragm if the distribution of intensity of light I(r ) on the screen is knows. Here r is the distance from the point P .
View SolutionA plane light wave with wavelength lambda = 0.65mum falls normally on a large glass plate whose opposite side has a large and an opaque strip of width a = 0.30mm (Fig.) A screen is placed at a distance b = 110 cm from the plate. The height h of the ledge is such that the intensity of light at point 2 of the screen is the heighest possible. making use of Fig. find the ratio of intensities at point 1 and 2 .
View SolutionA small hole P is made in a piece of cardboard. The hole is illuminated by a torch as shown in Fig. 16.3. The pencil of light coming out of the hole falls on a mirror. At which point should the eye be placed so that the hole can be seen?
View Solutionयंग के द्विक रेखा छिद्र प्रयोग में पर्दे के किसी बिन्दु पर पथान्तर होने पर वहाँ प्रकाश की तीव्रता K है प्रयुक्त प्रकाश की तरंगदैर्ध्य है ) तो पर्दे के उस बिन्दु पर जहाँ पथान्तर है। तीव्रता होगी:
View Solutionयंग के दो रेखा-छिद्रो वाले प्रयोग में जब D (छिद्र एवं परदे की बीच की दूरी ), यदि फ्रिंज की चौड़ाई से बहुत अधिक हो , तो व्यतिकरण फ़्रिंजो की आकृति होती है लगभग
View SolutionYou have 3 opaque strips with very small holes of different shapes as shown in Fig. 11.5. If you obtain an image of the sun on a wall through these holes, will the image formed by these holes be the same or different?
View SolutionFresnel diffraction is produced due to light rays falling on a small obstacle. The intensity of light at a point on a screen beyond an obstacle depends on
View Solution