A heavy round log is suspended at the ends on two ropes so that the distance between the points of suspension of the ropes is equal to the diameter of the log. The length of each vertical segment of the ropes is l.Determine the period T of small oscillations of the system in a vertical plane perpendicular to the log.
Let us mark the horizontal diameter AB = 2r of the log at the moment it passes through the equilibrium position.Let us now consider the log at the instant when the ropes on which it is suspended are deflected from the vertical by a small angle α Fig. 187. In the absence of slippage of the ropes we can easily find from geometrical considerations that the diameter AB always remains horizontal in the process of oscillations. Indeed if EF ⊥ DK FK = 2r tan α ≈ 2rα. But BD ≈ FK/2 ≈ rα. Consequently ∠BOD α as was indicated above. Since the diameter AB remains horizontal all the time the log performs translatory motion i.e. the velocities of all its points are the same at each instant. Therefore the motion of the log is synchronous to the oscillation of a simple pendulum of length I. Therefore the period of small oscillations of the log is
Related Solutions
A heavy round log is suspended at the ends on two ropes so that the distance between the points of suspension of the ropes is equal to the diameter of the log. The length of each vertical segment of the ropes is 1. Determine the period T of small oscillations of the system in a vertical plane perpendicular to the log.
View SolutionA 40 kg mass, hanging at the end fo a rope of length l, oscillates in a vertical plane with an angular amplitude theta_0. What is the tension in the rope when it makes en angle theta with the vertical ? If the breaking strength of the rope is 80kg, what is the maximum amplitude with which the mass can oscillate without the rope breaking?
View SolutionA body of mass 20 kg is suspended using two ropes. One of the ropes is to the vertical. What should be the inclination of the other rope with the vertical so that tension in this will be minimum ? Find the values of the tensions in the two strings also.
View SolutionA uniform rod of length L and weight W is suspended horizontally by two vertical ropes as shown. The first rope is attached to the left end of the rod while the second is attached to the left end of the rod while the second rope is attached a distance L//4 from the right end. The tension in the second rope is. .
View SolutionA mass M attached to the end of a small flexible rope of diameter d=1 cm is raised vertically by winding the rope on a reel. If the reel is turned uniformly ay the rate of n=2 rps, what will be the tension T in the rope? Neglect inertia of the rope and slight lateral motion of the suspended mass. (Fig.5.25)

View SolutionA rope of length L and mass 6kg is suspended from a rigid base. length of rope from free end 1/4 The value of tension in the rope at a distance will be:
View SolutionA thin rod of length 1 m is suspended from its end and is made to oscillate in a vertical plane. The distance between the point of suspension and centre of oscillation will be :
View SolutionTwo light ropes of equal length are tied at fixed points A and B of fixed, horizontal rods xy. A light bar is attached to both ropes in the same image as the equinox. With ropes rods 45^(@) Makes an angle. If Bob is displaced a little perpendicular to the bottom of the ropes, the resulting short oscillations will have a period of oscillation.
View Solutionएक कण उर्ध्वाधर तल में गति कर रहा है। यह 1 लम्बाई की रस्सी के एक सिरे से बधा है जिसका दूसरा सिरा जड़वत है। निम्नतम बिन्दु पर वेग u है। किसी भी स्थिति पर रस्सी में तनाव व कण का त्वरण है।
यदि
View SolutionA uniform rope of length L rests on a smooth plane. One end of the rope is pulled with a force F. what is the tension in the rope at a distance l from that end ?
View SolutionM द्रव्यमान के दो धातु के गोलों को L लम्बाई की दो रस्सियों से लटकाया गया है | गोलों के सिरों के मध्य दुरी L है तब, गोलों के परस्पर आकर्षण के कारण रस्सी का ऊर्ध्वाधर से बना कोण होगा
View SolutionA man is swinging on a swing made of 2 ropes of equal length L and in direction perpendicular to the plane of paper. The time period of the small oscillations about the mean position is
View Solution11 small ropes are cut from m long rope. Find the length of each of the small rope.
View SolutionA 40-kg mass hanging at the end of a rope of length l . Oscillates in a vertical plane with an angular of theta_(0) . What is the tension in the rope when it makes an angle theta with the vertial ? If the breaking strength of the rope is 80 kg, what is the maximum angular amplitude with which the mass can oscillate without the rope breaking ?
View SolutionA 5kg rope vertical rope with a force of 100N upward and 70N downward at the lower end is moving along the vertical line. What will be the tension in the middle of that rope -
View SolutionIf a transverse pulse is created at the topmost point of a uniform rope suspended vertically, then
View SolutionIf a transverse pulse is created at the topmost point of a uniform rope suspended vertically, then
View SolutionAn ellipse is interpreted by a rope without two ends, if the axis is 6 cm and 4 cm, then the required length of the rope and the distance between the two points are respectively (in cm).
View SolutionL लंबाई की एक रस्सी को F बल से खींचा जाता है । यदि जिस सिरे पर बल लगा है उससे x दूरी पर रस्सी में तनाव T है । तो T का मान है -
View SolutionA mass 1kg attached to the end of a flexible rope of diameter is raised vertically by winding the rope on a reel as shown. If the reel is turned uniformly at the rate of What is the tension in rope. The inertia of rope may be neglected.
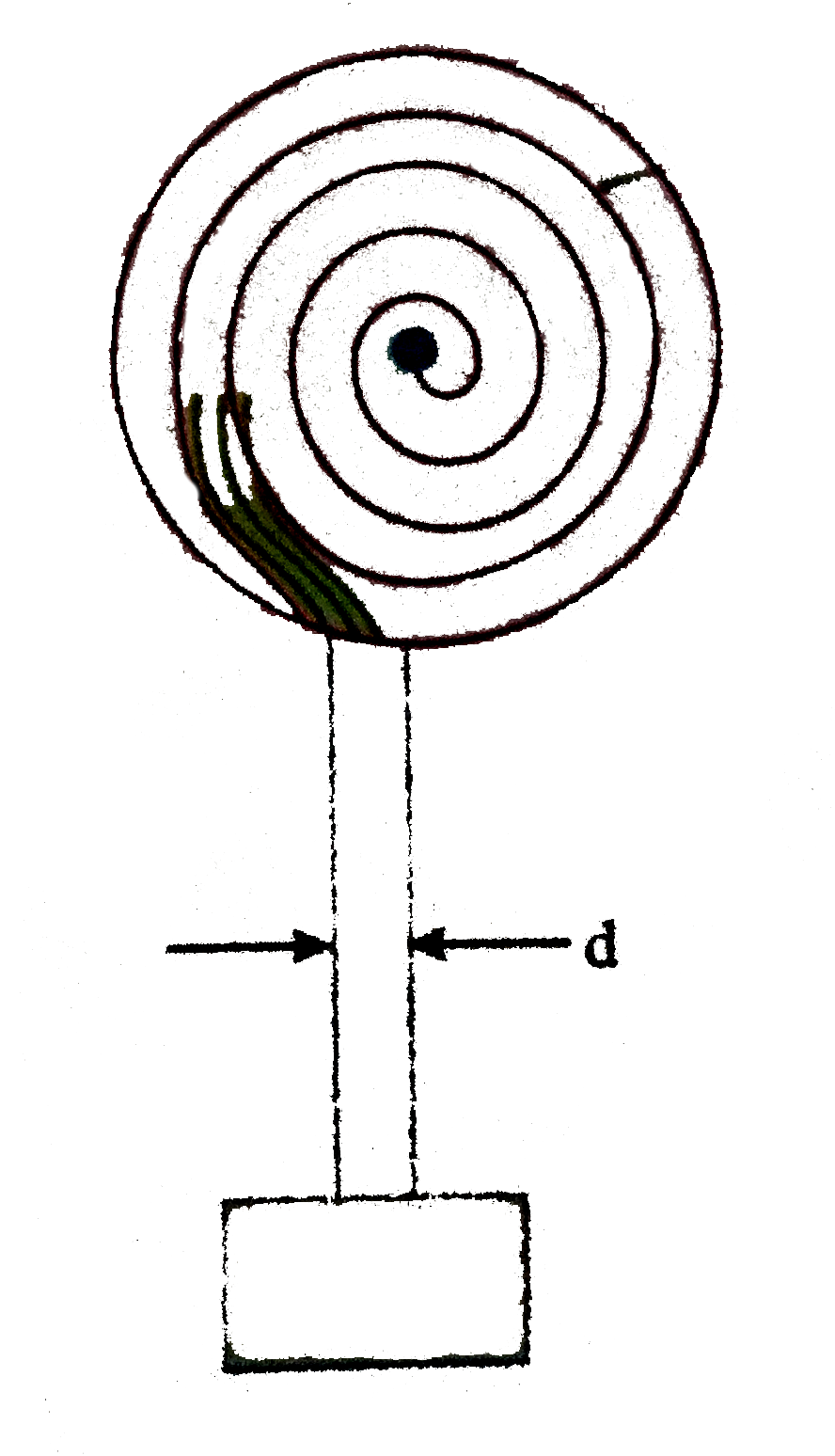
View Solution