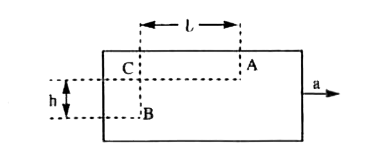
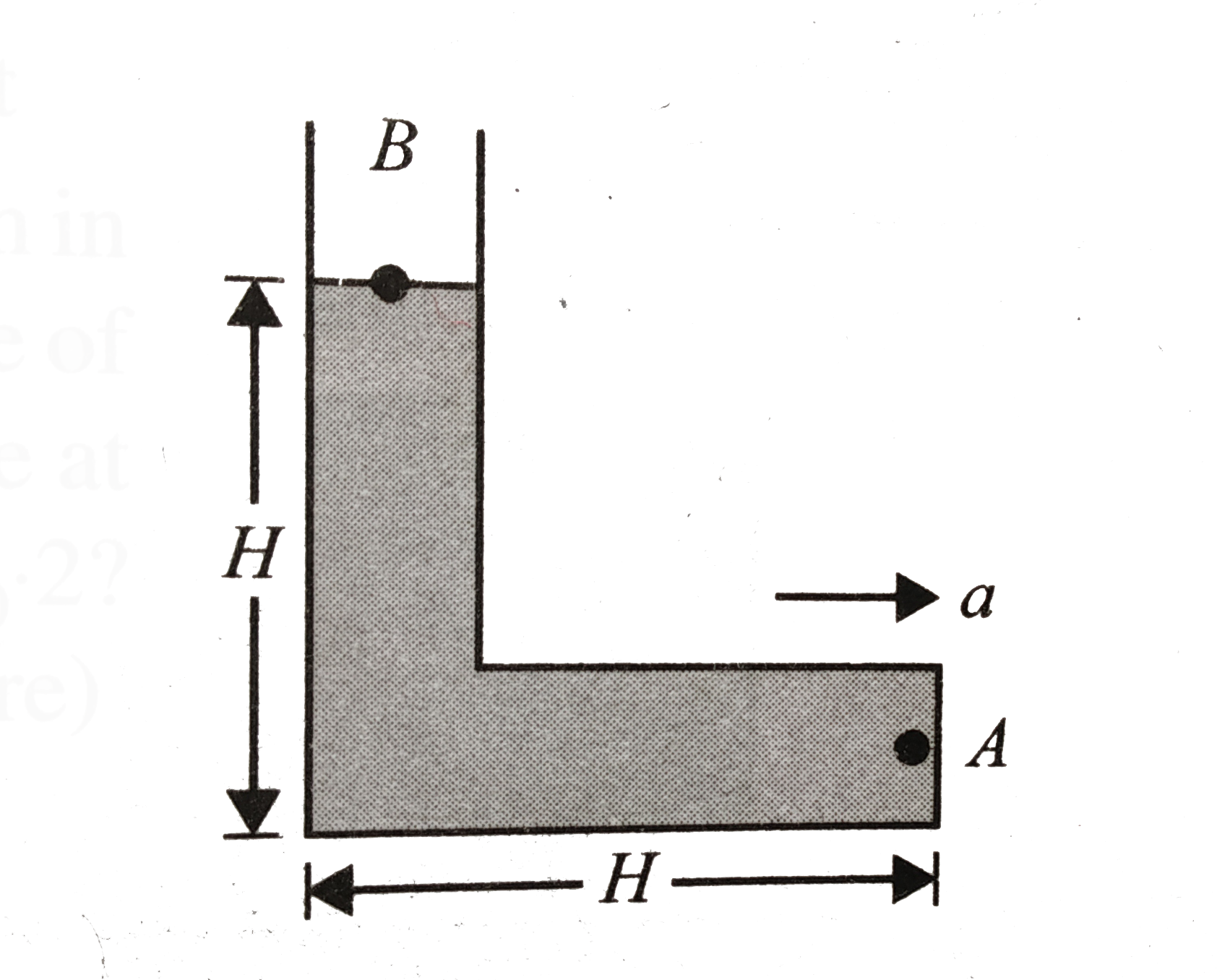
A rectangular container moves with an acceleration a along the positive direction as shown in figure . The pressure at the point A in excess of the atmospheric pressure P0 is take ρ as the density of liquida ρghb ρalc ρgh + ald Both a and c
Correct option b ρalExplanation :
Related Solutions
A rectangular container moves with an acceleration a along the positive direction as shown in figure. The pressure at the in excess of the atmospheric pressure is (take as the density of liquid)

View SolutionA rectangular container moves with an acceleration a along the positive direction as shown in figure. The pressure at the A in excess of the atmospheric pressure p_(0) is (take rho as the density of liquid)
View Solution
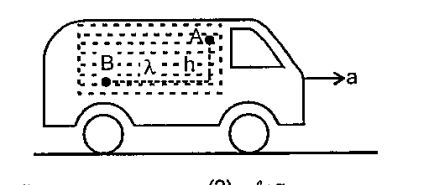
A sealed tank containing a liquid of density moves with a horizontal acceleration a, as shown in the figure. The difference in pressure between the points A and B is
View SolutionA sealed tank containing a liquid of density moves with a horizontal acceleration a, as shown in the figure. The difference in pressure between the points A and B is
View SolutionA sealed tank containing a liquid of density rho moves with a horizontal acceleration a, as shown in the figure. The difference in pressure between the points A and B is
View SolutionA sealed tank containing a liquid of density rho moves with a horizontal acceleration a, as shown in the figure. The difference in pressure between the points A and B is
View SolutionA tank compeltely filled with a liquid of density moves with an accelectrion a along horizontal direction, as shown in figure. The difference in pressure between the points A and B is
View SolutionA sealed tank containing a liquid of density rho moves with horizontal acceleration a as shown in the figure. The difference in pressure between two points A and B will be
View SolutionA sealed tank containing a liquid of density rho moves with horizontal acceleration a as shown in the figure. The difference in pressure between two points A and B will be
View SolutionA sealed tank containing a liquid of density moves with horizontal acceleration a as shown in the figure. The difference in pressure between two points and will be

View SolutionA L Shaped tube containing liquid of density pis accelerated horizontally with acceleration as shown in the figure. The end of tube B is closed while end A is open. If the atmospheric pressure is Po . Then the pressure at B is :
View SolutionAssertion: In the siphon shown in figure, pressure at P is equal to atmospheric pressure

Reason: Pressure at Q is atmospheric pressure and points P and Q are at same levels.
View SolutionAssertion: In the siphon shown in figure, pressure at P is equal to atmospheric pressure Reason: Pressure at Q is atmospheric pressure and points P and Q are at same levels.
View Solution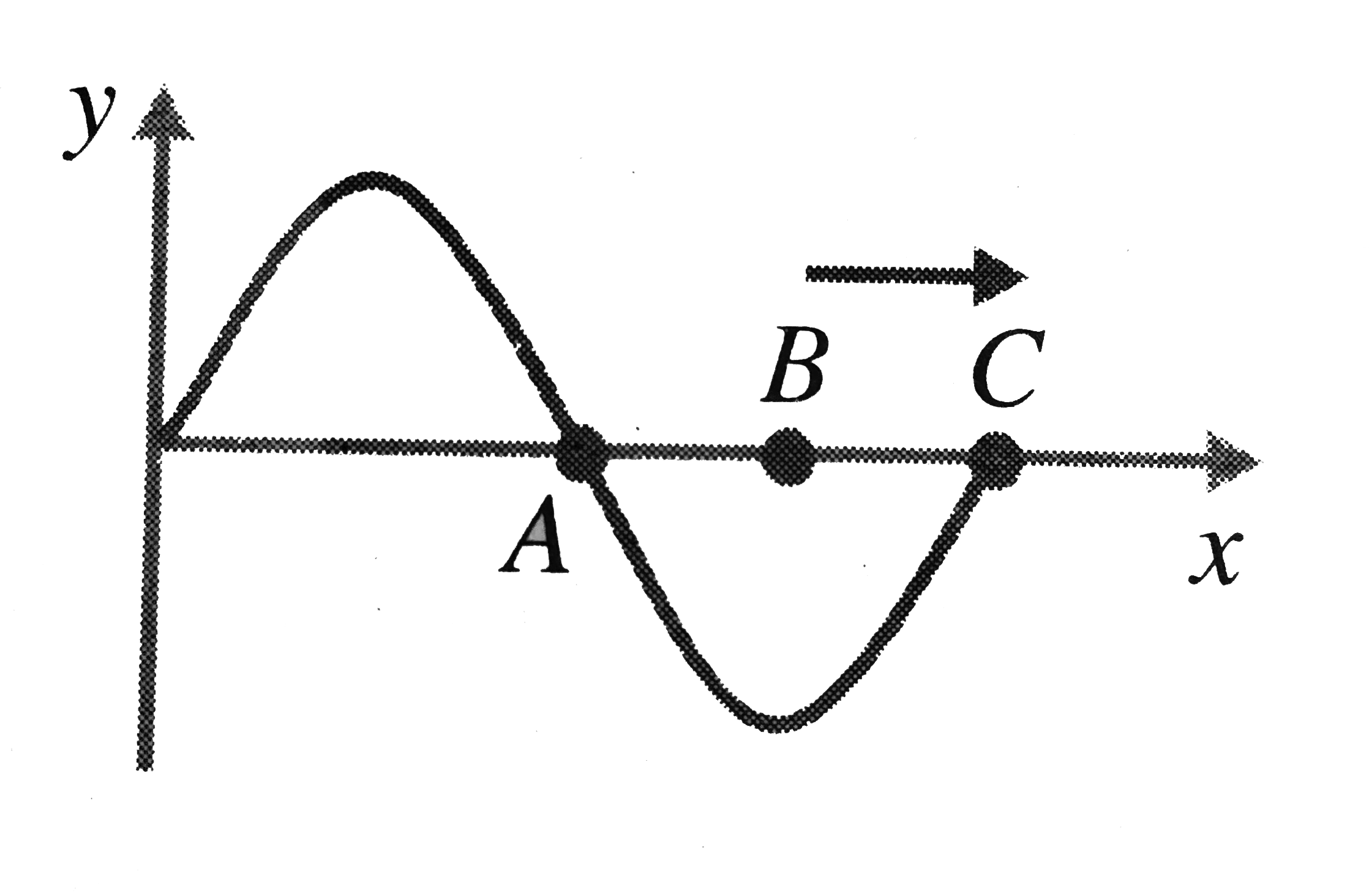
The figure shows an instantaneous displacement position graph of a sound wave travelling along the positive x-axis Identify the points of
i.Maximum pressure,
ii. Minimum pressure and
iii. Atmospheric pressure (or normal pressure.)
View Solution
The figure shows an instantaneous displacement position graph of a sound wave travelling along the positive x-axis Identify the points of
i.Maximum pressure,
ii. Minimum pressure and
iii. Atmospheric pressure (or normal pressure.)
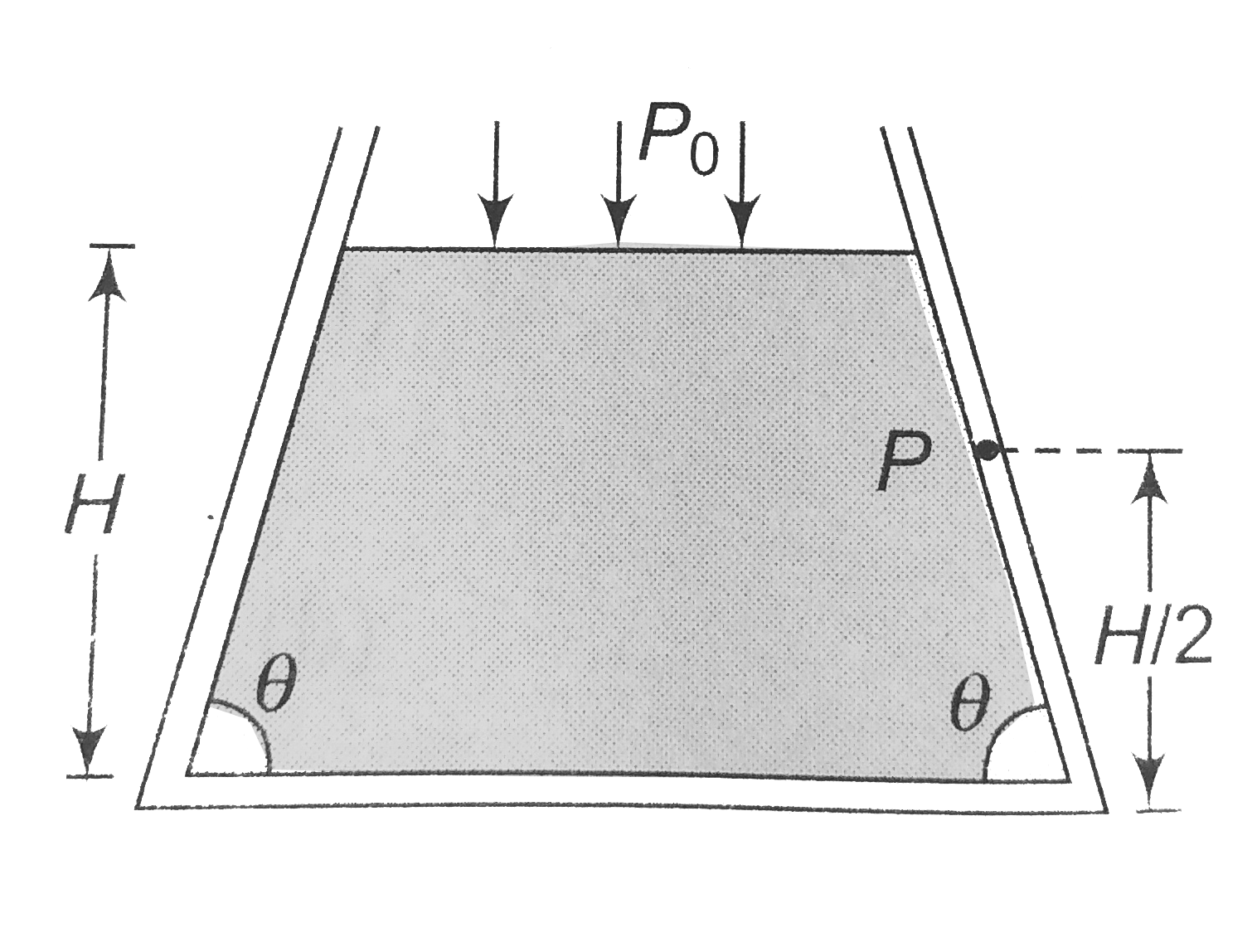
View SolutionA container shown in figure contains a liquid to depth H, and of density The gauge pressure at point P is :
View SolutionFor the L -shaped vessel shown in the figure, determine the value of acceleration a so that pressure at point A becomes equal to p_(0)/2 ? ( p_(0) is the atmospheric pressure)
View SolutionFor the -shaped vessel shown in the figure, determine the value of acceleration a so that pressure at point becomes equal to ? ( is the atmospheric pressure)
View Solutionif a vessel containing a fluid of density rho upto height h is accelerated vertically downwards with acceleration a_0 then the pressure by fluid at the bottom of vessel is ( P_0 to atmospheric pressure)
View SolutionA lift is moving upwar with a acceleretion a density of liquid is d and atmospheric pressure is p_0 . Then pressure at a point A at a depth h is
View Solution