From the conditions of the foregoing problem find:a normalized eigenfunctions of the particle in the states for which ψr depends only on r;b the most probable value rpr for the ground state of the particle and the probability of the particle to be in the region r < rpr.
a The nomalized wave functions are obtained from the normalizationb The radial probability distribution function isThe probability for the particle to be found in the region r < rpr is clearly 50 % as one can immediately see from a graph of sin2 x.
Related Solutions
From the condition of the foregoing problem find: (a) normalized eigenfunctions of the particle in the states for which Psi(r ) depends only on r , (b) the most probable value r_(pr) for the ground state of the particle and probability of the particle to be in in the region r lt r_(pr)
View SolutionMaking use of the solution of the foregoing problem, determine the probability of the particle with energy to be located in the region , if .
View SolutionFrom the conditions of the foregoing problem find :
(a) the number of molecules whose potential energy lies within the internal from to ,
(b) the most probable value of the potential energy of a molecule , compare this value with the potential energy of a molecule located at its most probable distance from the centre of the field.
View Solutionबीटा कण पर उपस्थित आवेश का मान बताइये।
View Solutionबीटा कण पर उपस्थित आवेश का मान बताईये |
View Solutionदो आवेशित कण A तथा B एक दूसरे को बल से प्रतिकर्षित करते हैं , जहाँ k एक अचर राशि हैं तथा r उनके बीच की दूरी हैं । कण Aको एक स्थान पर जड़कर रखा गया हैं । कण B , जिसका द्रव्यमान m हैं , A से दूरी से स्थिर अवस्था से छोड़ दिया जाता हैं । कणों पर सिर्फ उनके बीच के प्रतिकर्षण बल को प्रभावी मानें। (a) इन कणों की विद्युतीय स्थितिज ऊर्जा में परिवर्तन ज्ञात करें जब कण B की दूरी A से काफी अधिक हो जाती हैं । (b) इस स्थिति में B की चाल बताएँ ।
View SolutionThe potential energy of a particle in a force field is:
,. Where and are positive
constants and is the distance of particle from the centre of the field. For stable equilibrium the distance of the particle is
View Solution(A) : Moment of inertia of a particle changes with axis of rotation. (R ) : Moment of inertia depends on mass and distance of the particle from the axis of rotation.
View Solution(A) : Moment of inertia of a particle changes with axis of rotation. (R ) : Moment of inertia depends on mass and distance of the particle from the axis of rotation.
View Solutionબળક્ષેત્રમાં એક કણની સ્થિતિઊર્જા , જ્યાં A અને B ધન અચળાંકો છે અને r એ ક્ષેત્રના કેન્દ્રથી કણનું અંતર છે. સ્થાયી સમતોલનમાં કણનું અંતર r = ……. .
View SolutionA particle is released from the top of the smooth hemisphere R as shown. the normal contact between the particle and the hemisphere in position theta is
View SolutionIn a scale of match the particle with respect to their probable size:
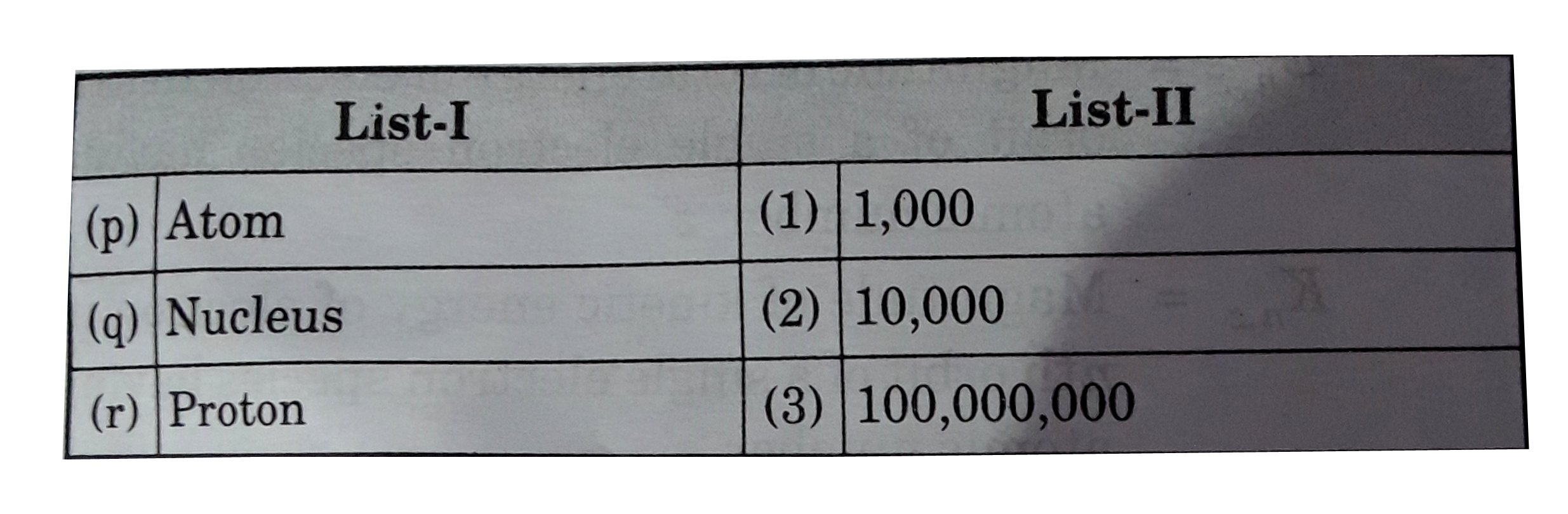
Codes :
p q r " "p q r
View SolutionFor the hydrogen atom in its ground state, calculate (a) the probability density y (r) and (b) the radial probability density Psi^(2)(r) for r= a, where a is the Bohr radius.
View Solution'' दो कणों के समूह की ...... केवल कणों के बीच की दूरी पर निर्भर करती हैं । ''उक्त वाक्य में रिक्त स्थान की पूर्ति के लिए सर्वाधिक सटीक चयन हैं ।
View SolutionThe potential energy of a particle in a conservative field is where a and b are positive constants and r is the distance of particle from the centre of field. For equilibrium, the value of r is
View SolutionThe potential energy of a particle in a conservative field is U =a/r^3-b/r^2, where a and b are positive constants and r is the distance of particle from the centre of field. For equilibrium, the value of r is
View SolutionThe potential energy of a particle in a conservative field is , where a and b are positive constants and r is the distance of particle from the centre of field. For equilibrium, the value of r is
View SolutionName the properties which depend only on the solute particles.
View Solutionदस कणों की मीटर/सेकण्ड में चाल क्रमशः 0,1,2,3,3,3,4,4,5 व 6 है । इन कणों के लिए सर्वाधिक प्रसम्भाव्य चाल ज्ञात कीजिए
View SolutionAssertion (A ) : The probability of finding an electron in a small volume around a point (x,y,z ) at a diatance r from the nucleus is proportional to . reason (R ) : subatomic particle have both wave and particle nature . The correct choice is
View Solution