Find the possible values of energy of a particle of mass m located in a spherically symmetrical potential well U r = 0 for r < r0 and U r = ∞ for r = r0 in the case when the motion of the particle is described by a wave function ψr depending only on r.Instruction. When solving the Schrodinger equation make the substitution ψr = x r/r.
The Schrodinger equation isFor r < r0 we have rejected a term B cos k r as it does not vanish at r = 0. Continuity of the wavefunction at r = r0 requires
Related Solutions
A particle of mass is located in a spherically symmetrical potential well for and for .
(a) By means of the substitution find the equation defining the proper values of energy of the particle for , when its motion is described by a wave function depending only on . Reduce that equation to the form
(b) Calculate the value of the quantity at which the first level appears.
View SolutionThe potential energy of a particle in a force field is:
,. Where and are positive
constants and is the distance of particle from the centre of the field. For stable equilibrium the distance of the particle is
View SolutionThe potential energy (U) of a particle can be expressed in certain case as U=(A^(2))/(2mr^(2))-(BMm)/(r) Where m and M are mass and r is distance. Find the dimensional formulae for constants.
View SolutionThe potential energy U of a particle in a field varies with position r as
Where a and b are positive constants. Find the position where the particle will be in stable equilibrium.
View SolutionA particle with kinetic energy T is deflected by a spherical potential well radius R and depth U_(0) i.e., by the field in which the potential energy of the particle takes the form U = {(0" for "r gt R),(-U_(0)" for "r lt R):} where r is the distance from the centre of the well. Find the relationship between the aiming parameter b of the particle and the angle theta through which it deflects from initial motion direction.
View SolutionPotential energy in a field is given by then find the value of r for equilibrium position.
View SolutionPotential energy in a field is given by then find the value of r for equilibrium position.
View SolutionThe potential energy of a two particle system separated by a distance r is given by U(r ) =A/r where A is a constant. Find to the radial force F_(r) , that each particle exerts on the other.
View SolutionThe potential energy of a two particle system separated by a distance r is given by U(r ) =A/r where A is a constant. Find to the radial force F_(r) , that each particle exerts on the other.
View SolutionThe potential energy of a particle in a conservative field is where a and b are positive constants and r is the distance of particle from the centre of field. For equilibrium, the value of r is
View SolutionThe potential energy of a particle in a conservative field is U =a/r^3-b/r^2, where a and b are positive constants and r is the distance of particle from the centre of field. For equilibrium, the value of r is
View SolutionThe potential energy of a particle in a conservative field is , where a and b are positive constants and r is the distance of particle from the centre of field. For equilibrium, the value of r is
View SolutionA spherical conductor having charge q and radius r is placed at the centre of a spherical shell of radius R and having charge . The potential difference between the two is
View SolutionThe mass density of a spherical body is given by of where r is the distance r from the centre. The correct graph that describes qualitatively the acceleration, a, of . a test particle as a function of r is :
View SolutionIf is the interatomic distance, and are positive constants, denotes potential energy which is a function dependent on as follows :
.
The equilibrium distance between two atoms is
View SolutionIn a hollow spherical shell potential (V) changes with respect to distance (r0 from centre [ V_("inside")=(Q)/(4pi epsi_(0)R)r lt R, V_("outside")=(Q)/(4pi epsi_(0)r) r gt R V alpha (1)/(2)]
View SolutionA sphere of density and radius a has a concentric of radius b as shown in the
(a) Sketch the gravitational force exerted by the spehre on the particle of mass m located at a distance r from the centre of the sphere as a function of r in the range
(b) Sketch the corresponding curve for the potential energy u (r) of the system
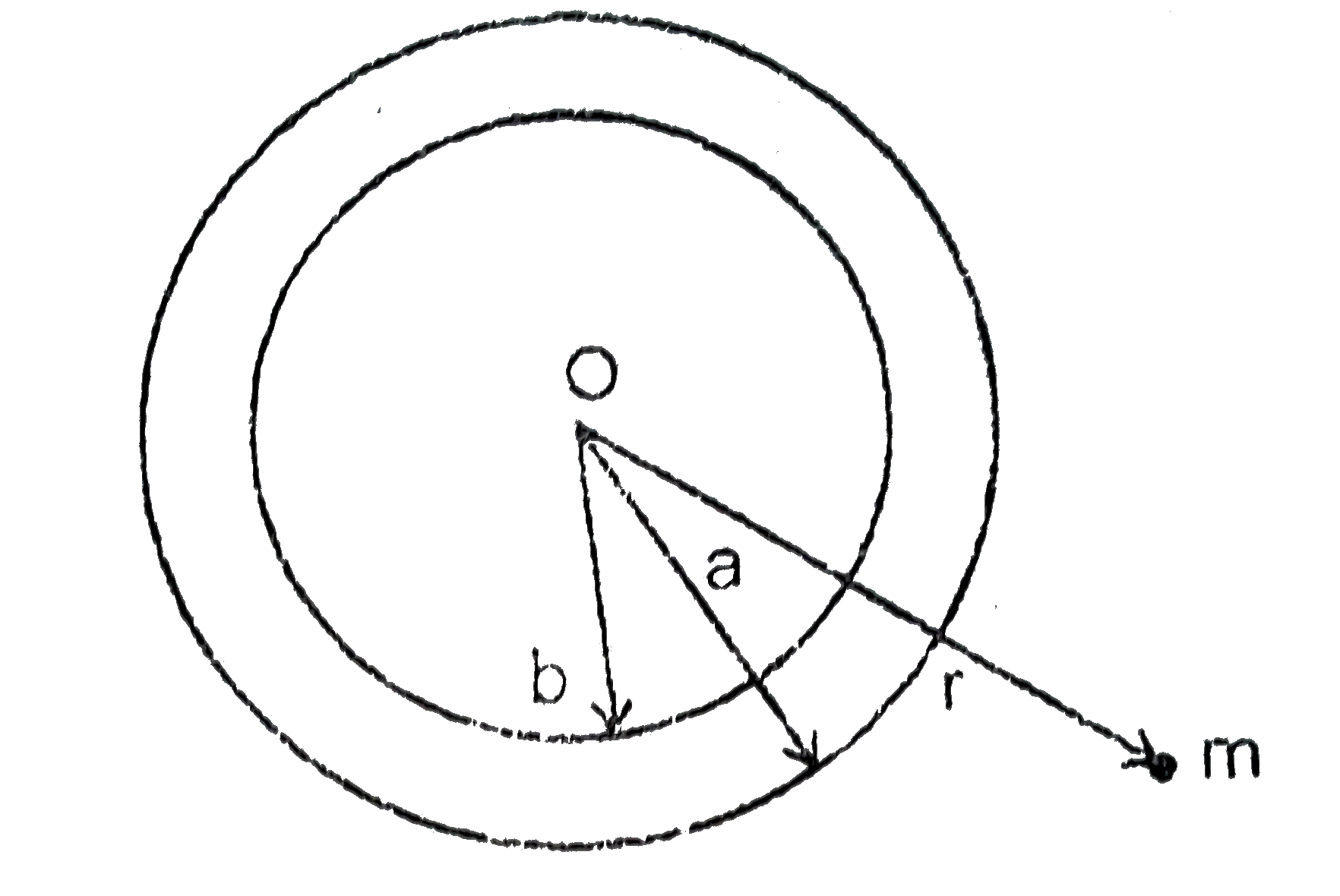 ,
,
View SolutionA sphere of density rho and radius a has a concentric of radius b as shown in the (a) Sketch the gravitational force exerted by the spehre on the particle of mass m located at a distance r from the centre of the sphere as a function of r in the range 0 le r le oo (b) Sketch the corresponding curve for the potential energy u (r) of the system ,
View SolutionThe potential energy U of a particle in a field varies with position r as
where a and b are positive constants. Find the positions, where the particle:will be in stable equilibrium.
View SolutionShow that the logarithmic function given by is a bijection.
View Solution