A side wall of a wide open tank is provided with a narrowing tube Fig. 1.88 through which water flows out. The cross-sectional area of the tube decreases from S = 3.0 cm2 to s = 1.0 cm2. The water level in the tank is h = 4.6 m higher than that in the tube.Neglecting the viscosity of the water find the horizontal component of the force tending to pull the tube out of the tank.
Suppose the radius at A is R and it decreases uniformaly to r at B where S = πR2 and s = πr2 . Assume also that the semi-vertical angle at 0 is α. Thenwhere y is the radius at the point P distant x from the vertex O. Suppose the velocity with which the liquid flows out is V at A v at B and u at P. Then by the equation of continuitywhere Pp is the pressure at P and Po is the atmospheric pressure which is the pressure just outside of B. The force on the nozzle tending to pull it out is thenWe have subtracted Po which is the force due to atmosphenic pressure the factor sinθ gives horizontal component of the force and ds is the length of the element of nozzle surface ds = dx sec θ and If we try to calculate F from the momentum change of the liquid flowing out will be wrong even as regards the sign of the force. There is of course the effect of pressure at S and s but quantitative derivation of F from Newtons law is difficult.
Related Solutions
A side wall of a wide open tank is provided with a narrowing tube through which water flows out. The cross-sectional area of the tube decreases from to . The water level in the tank is heigher than in the tube. Neglecting the viscosity of water, find the horizontal component of the force tending to pull the tube out of the tank.
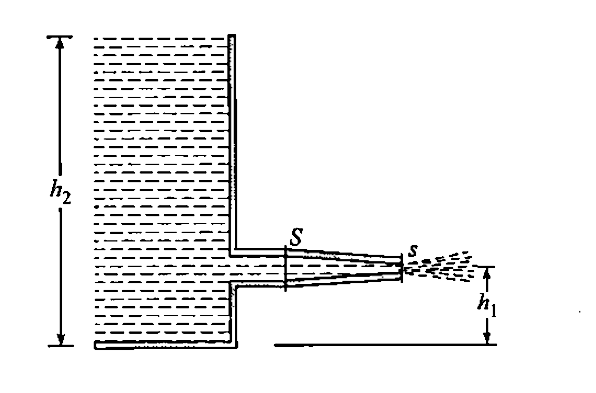
View SolutionA side wall of a wide open tank is provided with a narrowing tube (figure) through which water flows out. The cross-sectional area of the tube decreases from S=3.0cm^2 to s=1.0cm^2 . The water level in the tank is h=4.6m higher than that in the tube. Neglecting the viscosity of the water, find the horizontal component of the force tending to pull the tube out of the tank.
View SolutionWater flows through the tubes shown in figure. The areas of cross-section of the wide and the narrow portions of the tube are and respectively. The rate of flow of water through the tube is . Find the difference of mercury levels in the U-tube.
View SolutionA steam of water flowing horizontally with a speed of 25m ^(s-1) gushes out of a tube of cross-sectional area 10^(-3) m^(2) , and hits at a vertical wall nearby. What is the force exerted on the wall by the impact of water
View SolutionWater flows through the tube shown in figure. The areas of cross section of the wide and the narrow portions of the tube are respectively. The rate of flow of water through the tube is . Find the difference of mercury levels in the U-tube.
View SolutionWater flows through the tube shown in figure. The areas of cross section of the wide and the narrow portions of the tube are respectively. The rate of flow of water through the tube is . Find the difference of mercury levels in the U-tube.

View SolutionWater flows through the tube shown in figure. The areas of cross section of the wide and the narrow portions of the tube are respectively. The rate of flow of water through the tube is . Find the difference of mercury levels in the U-tube.

View SolutionWater flows through the tube shown in figure. The areas of cross section of the wide and the narrow portions of the tube are respectively. The rate of flow of water through the tube is . Find the difference of mercury levels in the U-tube.

View SolutionAn open cubical tank completely filled with water is kept on a horizontal surface. Its acceleration is then slowly increasesd to as shown in the figure. The side of the tank is 1m. Find the mass of water that would spill out of the tank.

View SolutionThrough a horizontal tube of non-uniform cross section water is flowing a uniform rate. Pressure of water at any point in the tube is and velocity of water flow is 0.6 m. . If the velocity of water flow at another point in the tube is 9 m. , then what is the pressure there?
View SolutionA large cylindrical tank has a hole of area A at its bottom. Water is poured in the tank by a tube of equal cross sectional area A ejecting water at the speed v.
View SolutionA large cylindrical tank has a hole of area A at its bottom. Water is poured in the tank by a tube of equal cross-sectional area A ejecting water at the speed v.
View SolutionA large cylindrical tank has a hole of area A at its bottom. Water is poured in the tank by a tube of equal cross-sectional area A ejecting water at the speed upsilon .
View SolutionA large cylindrical tank has a hole of area A at its bottom. Water is poured in the tank by as tube of equal cross sectional area A ejecting water at the speed v.
View SolutionA large cylindrical tank has a hole of area A at its bottom. Water is oured in the tank by a tube of equal cross sectional area A ejecting water at the speed v.
View SolutionA large cylindrical tank has a hole of area A at its bottom. Water is oured in the tank by a tube of equal cross sectional area A ejecting water at the speed v.
View Solutionઆડછેદનું ક્ષેત્રફળ ધરાવતી એક નળીમાં ની ઝડપ સમક્ષિતિજ વહન કરતા પાણીના પ્રવાહમાંથી પાણી બહાર ધસી આવીને નજીકની ઊર્ધ્વ દીવાલને અથડાય છે . પાણીની અસરથી દીવાલ પર લાગતું બળ કેટલું હશે ? પાણી પાછું ફેંકાતું ( rebound ) નથી તેમ ધારો .
View SolutionWater filled in an empty tank of area 10 A through a tap of cross sectional area A. The speed of water flowing out of tap is given by v(m/s) =10(1-sin((pi)/(30)t) where t is in second. The height of water level from the bottom of the tank at t=15 second will be:
View SolutionWater filled in an empty tank of area 10 A through a tap of cross sectional area A. The speed of water flowing out of tap is given by v(m/s) =10(1-sin((pi)/(30)t) where t is in second. The height of water level from the bottom of the tank at t=15 second will be:
View SolutionWater filled in an empty tank of area 10 A through a tap of cross sectional area A. The speed of water flowing out of tap is given by v(m/s) =10(1-sin((pi)/(30)t) where t is in second. The height of water level from the bottom of the tank at t=15 second will be:
View Solution