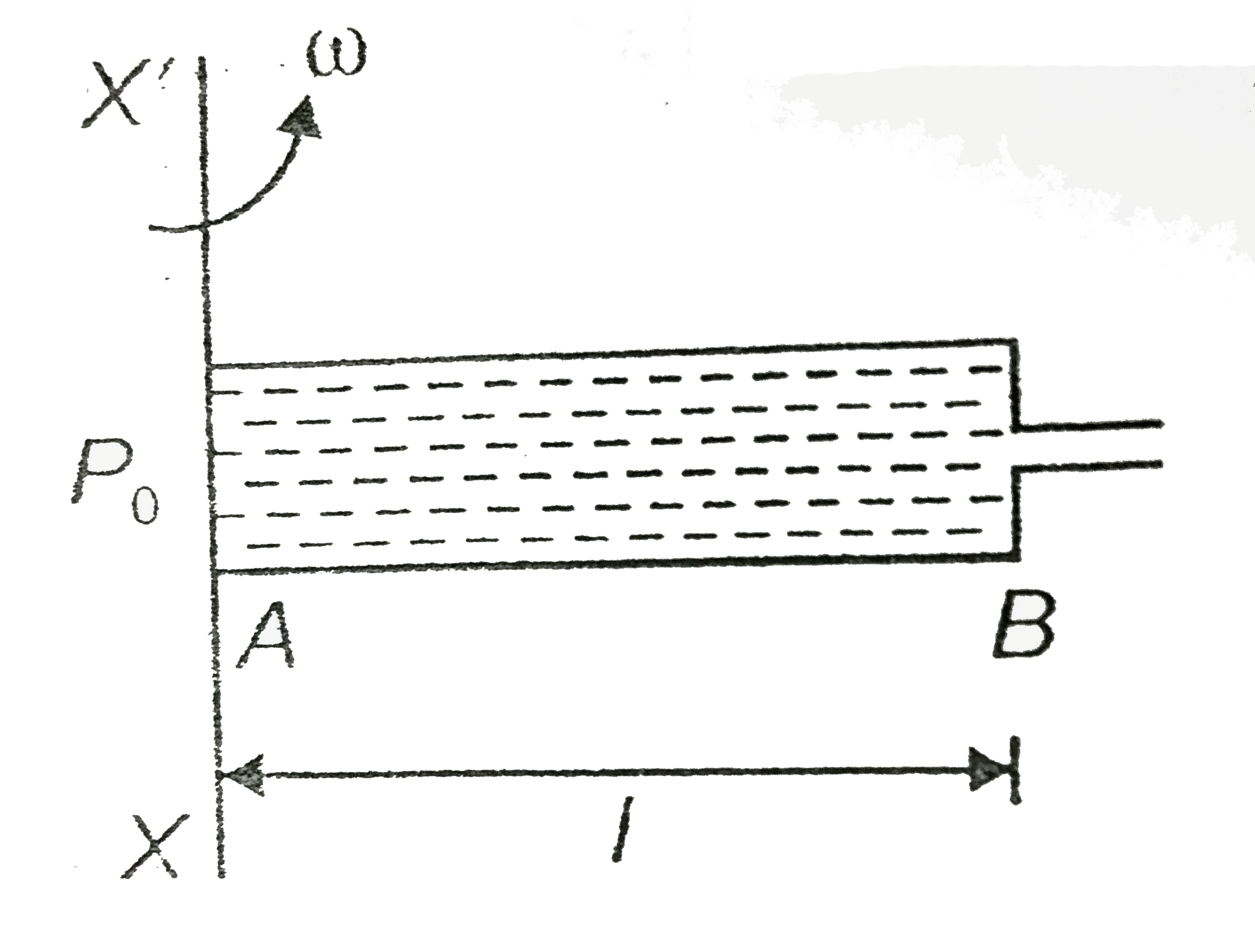
A horizontally oriented tube AB of length l rotates with a constant angular velocity ω about a stationary vertical axis OO passing through the end A Fig. 1.86. The tube is filled with an ideal fluid. The end A of the tube is open the closed end B has a very small orifice. Find the velocity of the fluid relative to the tube as a function of the column height h.
In a rotating frame with constant angular velocity the Eulerian equation is In the frame of rotating tube the liquid in the column* is practically static because the orifice is sufficiently small. Thus the Eulerian Eq. in projection form along vector r which is the position vector of an arbitrary liquid element of length dr relative to the rotation axis reduces toThen applying Bemouirs theorem at the orifice for the points just inside and outside of the end B
Related Solutions
A horizontally oriented tube AB of length l rotates with a constant angular velocity omega about a stationary vertical axis OO^' passing through the end A (figure). The tube is filled with an ideal fluid. The end A of the tube is open, the closed end B has a very small orifice. Find the velocity of the fluid relative to the tube as a function of the column "height" h.
View SolutionA horizontal oriented tube AB of length l rotates with a constant angular velocity omega about a stationary vertical axis OO' passing thorugh the end A figure. The tube is filled with an ideal fluid. The end A of the tube is open, the closed end B has a very small orifice. find the velocity of the fluid relative to the tube as a function of the column height h.
View SolutionA horizontally orientd tube of length l rotates with a constant angular velocity omega about a stationary vertical axis. XX passing through end A. The tube is filled with ideal fluid. The end A of tube is having pressure P_(0) . The closed end B has a small hole and at time t = 0, the fluid column has length of l. Find velocity of fluid relative to tube at the instant t = 0
View SolutionA horizontally orientd tube of length l rotates with a constant angular velocity about a stationary vertical axis. XX passing through end A. The tube is filled with ideal fluid.
The end A of tube is having pressure . The closed end B has a small hole and at time t = 0, the fluid column has length of l. Find velocity of fluid relative to tube at the instant t = 0
View Solution_S01_079_Q01.png)
A horizontal oriented tube AB of length 5m rotates with a constant angular velocity 0.5 rad/s about a stationary vertical axis OO' passing through the end A. the tube is filled with ideal fluid. The end of the tube is open, the closed end B has a very small orifice. The velocity with which the liquid comes out from the hole (in m/s) is
View Solution_S01_079_Q01.png)
A horizontal oriented tube AB of length 5m rotates with a constant angular velocity 0.5 rad/s about a stationary vertical axis OO' passing through the end A. the tube is filled with ideal fluid. The end of the tube is open, the closed end B has a very small orifice. The velocity with which the liquid comes out from the hole (in m/s) is
View Solution_S01_079_Q01.png)
A horizontal oriented tube AB of length 5m rotates with a constant angular velocity 0.5 rad/s about a stationary vertical axis OO' passing through the end A. the tube is filled with ideal fluid. The end of the tube is open, the closed end B has a very small orifice. The velocity with which the liquid comes out from the hole (in m/s) is
View SolutionA horizontally oriented bent thin tube of length rotates with a constant angular velocity about a stationary vertical axis passing through the end as shown in figure. The portion of tube is parallel to and its length is equal . At , part of tube is filled with an ideal fluid. The end of tube is open, the closed end has a very small orifice. Find the maximum height reached by fluid relative to end . (take and )

View SolutionL लम्बाई की एक नली को एक असंपीड्य द्रव से पूरा भरकर इसे दोनों सिरों से बंद कर दिया गया है । बंद द्रव का द्रव्यमान M है । इस नली को एक क्षैतिज तल में नली के एक सिरे के परितः अचर कोणीय वेग से घुमाया जाता है । द्रव द्वारा नली के दूसरे सिरे पर क्रियाकारी बल होगा -
View SolutionA horizontally oriented tube AB of length l rotates with a constant angular velocity about a stationary vertical axis passing through the end A (figure). The tube is filled with an ideal fluid. The end A of the tube is open, the closed end B has a very small orifice. Find the velocity of the fluid relative to the tube as a function of the column "height" h.

View SolutionA horizontal tube of length closed at both ends contains an ideal gas of molecular weight M. The tube is rotated at a constant angular velocity m about a vertical axis passing through an end, Assuming the temperature to be uniform and constant, pressure P at the free end is___ (pressure at fixed end is )
View Solutionलम्बाई L वाली एक नलिका को किसी असंपीडिय द्रव से भर कर दोंनो तरफ से बंद कर दिया जाता है। तब इस नलिका के एक छोर से इसको क्षैतिज तल में एक समान कोणीय वेग से घुमाया जाता है। द्रव द्वारा दूसरे छोर पर लगाया गया बल है :
View SolutionL लम्बाई की एक नलिका M द्रव्यमान के असंपीड्य द्रव से पूर्णतया भरी है दोनों सिरों से बंद है। नलिका को उसके एक सिरे के परितः एकसमान कोणीय वेग से क्षैतिज तल से घुमाया जाता है। नलिका में भरे द्रव द्वारा दूसरे सिरे पर आरोपित बल का मान है
View SolutionLength of a horizontal arm of U-tube is L and ends of both the vertical arms are open to atompsheric pressure P_(0) , A liquid of density rho is poured in the tube such that liquid just fills the horizontal part of the tube as shown in figure . Now one end of the opened ends is sealed and the tube is then rotated about a vertical axis passing through the other vertical arm with angular speed omega_(0) . if length of each vertical arm is a and in the sealed end liquid rises to a height y, find pressure in the sealed tube during rotation.
View SolutionA tube of length L is filled completely with an incompressible liquid and it is closed at both the ends. The mass of the closed liquid is M. This tube is propelled in a horizontal plane with a constant angular velocity relative to one end of the tube. omega being rotated from. The force acting on the other end of the tube by the liquid will be:
View SolutionA tube of length 'L' is filled completely with an in compressiblem liquid of mass 'M' and closed at both ends. The tube is then rotated in a horizontal plane about one of it's ends with a uniform angular velocity . Then which of following statements are true :
View SolutionA tube of length L is completely filled with an incompressible liquid of mass M and is closed at both the ends. The tube is then thrown in a horizontal plane with a uniform angular velocity about one of its ends. omega is rotated with. The force exerted by the fluid at the other end is
View Solutionएक क्षैतिज नली, जिसके सिरे की त्रिज्या R है, में कोई द्रव v वेग से प्रवेश करता है । नली के दुसरे सिरे पर एक टोंटी लगी है जिसमे N छिद्र है, प्रत्येक छिद्र की त्रिज्या r है । छिद्र से निकलने वाले द्रव का वेग ज्ञात कीजिए ।
View SolutionA tube in vertical plane is shown in figure. It is filled with a liquid of density rho and its end B is closed. Then the force exerted by the fluid on the tube at end B will be : [Neglect atmospheric pressure and assume the radius of the tube to be negligible in comparison to l ]
View SolutionA tube in vertical plane is shown in figure. It is filled with a liquid of density rho and its end B is closed. Then the force exerted by the fluid on the tube at end B will be: [Assume the radius of the tube to be negligible in comparison to l]
View Solution