The potential energy U of diatomic molecules as a function of separation r is shown in figure. Identify the correct statement.a The atoms are in equilibrium if r = OAb The force is repulsive only if r lies between A and Bc The force is attractive if r lies between A and B d The atoms are in equilibrium if r = OB
Correct option d The atoms are in equilibrium if r = OBExplanation :System is bound or force is attractive when potential energy is negative.
Related Solutions
The potential energy function for the force between two atoms in a diatomic molecule is approximate given by , where and are constants and is the distance between the atoms. If the dissociation energy of the molecule is is
View SolutionThe potential energy U of two atoms of a diatomic molecule as a function of distance r between the atoms as shown in the given figure.
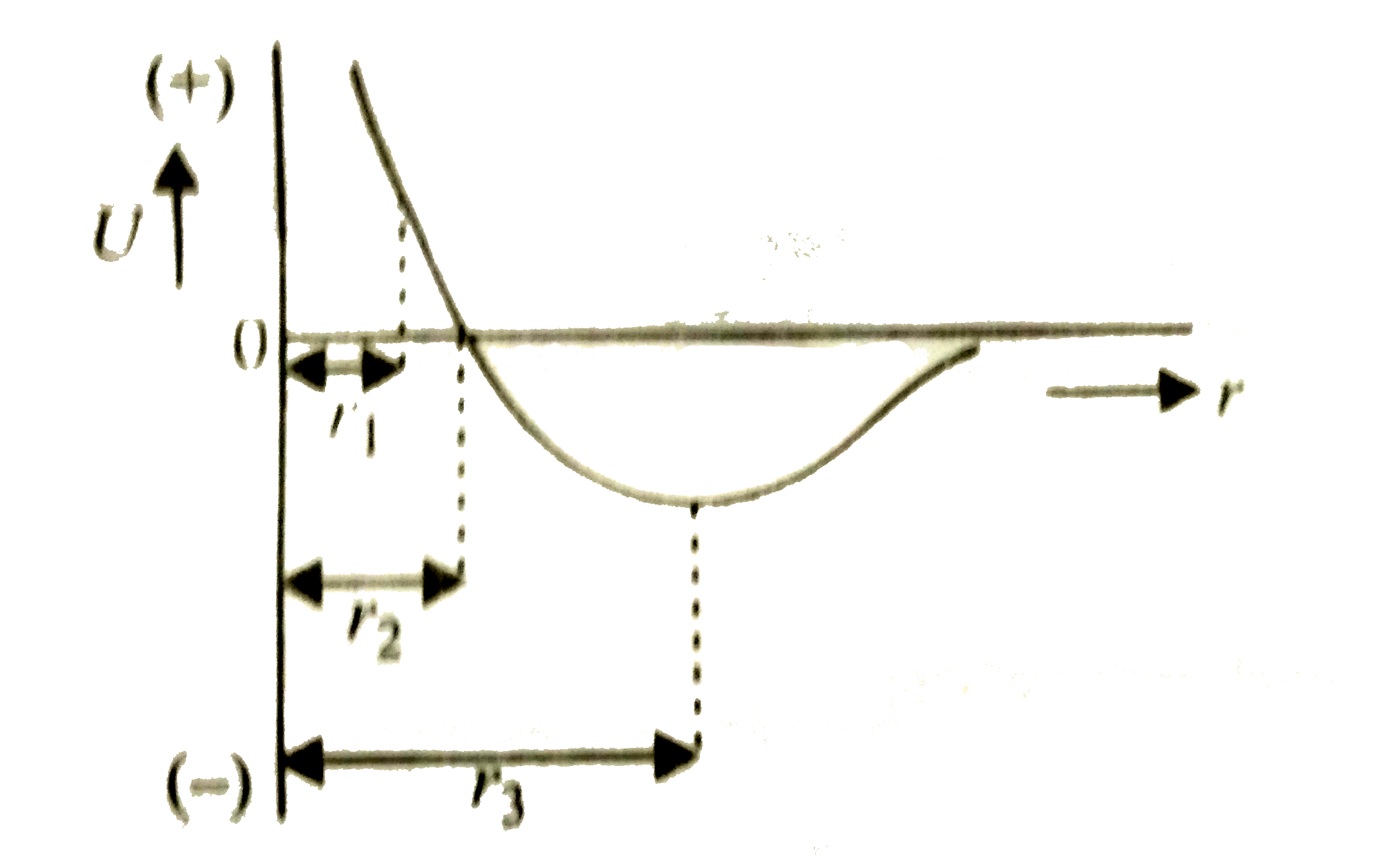
Read the following statement carefully.
1. The equilibrium separation distance between the atoms is equal to .
2. At , the force between the atom is repulsive.
. For, the force between the atoms is attractive
Which of the above statements is true ?
View SolutionThe potential energy U of two atoms of a diatomic molecule as a function of distance r between the atoms as shown in the given figure. Read the following statement carefully. 1. The equilibrium separation distance between the atoms is equal to r_(2) . 2. At r = r_(1) , the force between the atom is repulsive. 3. For r gt r_(2) , the force between the atoms is attractive Which of the above statements is true ?
View Solutionपरमाणुओं के मध्य दूरी r के फलन के रूप में किसी द्विपरमाण्विक अणु के दो परमाणुओं की स्थितिज ऊर्जा U को नीचे दिए गए चित्र के अनुसार दर्शाया गया है।
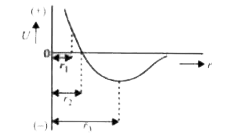
निम्न कथनों को सावधानीपूर्वक पढ़ें।
1. परमाणुओं के मध्य संतुलन पृथक्करण दूरी के बराबर होता है।
2. पर, परमाणु के मध्य बल प्रतिकर्षी होता है।
3. के लिए, परमाणुओं के मध्य बल आकर्षी होता है।
उपरोक्त कथनों में से कौन-सा सही है?
View SolutionThe potential energy U of diatomic molecules as a function of separation r is shown in figure. Identify the correct stateement.
View SolutionThe potential energy U of diatomic molecules as a function of separation r is shown in figure. Identify the correct stateement.
View SolutionIf the potential energy between two molecules is given by U= -(A)/(r^6) + B/(r^(12)) , then at equilibrium , separation between molecules , and the potential energy are :
View SolutionIf the potential energy between two molecules is given by U= -(A)/(r^6) + B/(r^(12)) , then at equilibrium , separation between molecules , and the potential energy are :
View SolutionForce between the atoms of a diatomic molecule has its origin in the interactions between the electrons and the nuclei present in each atom. This force is conservative and associated potential energy U(r) is, to a good approximation, represented by the Lennard - Jones potential. U (r) = U_(0) {((a)/(r))^(12) - ((a)/(r))^(6)} Here r is the distance between the atoms and U_(0) and a are positive constants. Develop expression for the associated force and find the equilibrium separation between the atoms.
View SolutionIf the potential energy between two atoms is U=(A)/(r^(12)) - (B)/(r^(6)) then the binding energy in equilibrium position is
View SolutionIf the potential energy between two atoms is U=(A)/(r^(12))=(B)/(r^(6)) then the binding energy in equilibrium position is
View SolutionIf is the interatomic distance, and are positive constants, denotes potential energy which is a function dependent on as follows :
.
The equilibrium distance between two atoms is
View SolutionThe given curve shows the change of mutual potential energy (U) with distance r between two particles at a distance r from each other, then which of the following statements is true? (i) B and D are equilibrium points. (ii) Point C is the point of stable equilibrium. (iii) The force of attraction between the points C and D on the curve is the force of attraction and the force of attraction between the points D and E is the force of repulsion. (iv) The force of repulsion between the points E and F on the curve is the force of repulsion.
View SolutionR is the interatomic distance, a and b are positive constants, u denotes potential energy which is a function dependent on R as follows .The equilibrium distance between two atoms is
View SolutionThe potential energy U between two atoms in a diatomic molecule is the distance between the atoms? as a function of as shown in the attached figure. Atoms are:
View SolutionChemical bond results when between combining atoms :
= attraction force
=repulsion forces
P.E. = potential energy
View SolutionIf the potential energy of two molecules, U = (A)/(r^(12))-(B)/(r^(6)) If it is, it will have potential energy at equilibrium.
View SolutionThe potential energy of a diatomic molecule is given as U = (a)/(x^(12)) - (b)/(x^(6)) . Find the (i) stable equilibrium distance of separation between two atoms, (ii) force on each atom as the function of separating distance x.
View Solutionthe points of maximum and minimum attraction in the curve between potential energy (U) and distance (r) of a diatomic molecules aree respectively.
View SolutionA particle of mass m lies at a distance r from the centre of earth. The force of attraction between the particle and earth as a function of distance is F(r ),
View Solution