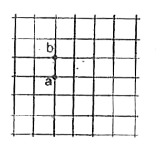
There is an infinite wire grid with square cells Fig. 3.38. The resistance of each wire between neighbouring joint connections is equal to R0. Find the resistance R of the whole grid between points A and B. Instruction. Make use of principles of symmetry and superposition.
Suppose that the voltage V is applied between the points A and B then V = IR = I0 R0 where R is resistance of whole the grid l0 the current through the grid and I the current through the segment AB. Now from symmetry I/4 is the part of the current flowing through all the four wire segments meeting at the point A and similarly the amount of current flowing through the wires meeting at B is also I/4. Thus a current I/2 flows through the conductor AS i.e. I0 = I/2Hence R = R0/2
Related Solutions
There is an infinite wire grid with square cells (Fig). The resistance of each wire between neighbouring joint connections is equal to R_(0) . Find the resistance R of the whole grid between points A and B . Instruction. Make use of principles of symmetry and superposition.
View SolutionThere is an infinite wire grid with cells in the form of equilateral triangles. The resistance of each wire between neighboring joint connections is R_0 The net resistance of the whole grid between the points A and B as shown in fig.
View SolutionThere is an infinite wire grid with cells in the form of equilateral triangles. The resistance of each wire between neighboring joint connections is R_0 The net resistance of the whole grid between the points A and B as shown in fig.
View SolutionA finite square grid, each link having resistance r, is fitted in a resistance less conducing circular wire. Determine the equivalenet resistance between A and B ("in" Omega) if r = (80//7) Omega .
View SolutionA finite square grid, each link having resistance r, is fitted in a resistance less conducing circular wire. Determine the equivalenet resistance between A and B ("in" Omega) if r = (80//7) Omega .
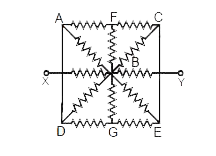
View SolutionThe given infinite grid consists of hexagonal cell of six resistor each of resistance R . Then R_(12) is equal to
View SolutionInfinite square brackets have been made by a infinitely long wire as shown. Between each junction, the resistance is r. Find equivalent resistance between points a and b
View SolutionThe sides of a square ABCD are formed of wires, each of resistance r and B is joined to D by a wire of resistance 2r. Find the equivalent resistance of the skelton
(i) between B and D, (ii) between A and C and (iii) between A and B.
View SolutionThe resistance of each side of the square (the smallest one) in the shown wire frame is R. The point is the equivalent resistance of the circuit between A and B.
View SolutionFour wires of equal length and of resistance each are connected square.
The equivalent resistance between two opposite corners is
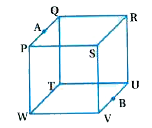
View SolutionA cube is constructed by connecting 12 wires of equal resistance as shown in figure. The equivalent resistance between the points A and B shown in the figure is..... . The resistance of each wire is of r . A and B are the midpoints of the sides PQ and VU respectively.
View SolutionThe given infinite grid consists of hexagonal cells of six resistors each of resistance R. then R_(12)
View SolutionThe given infinite grid consists of hexagonal cells of six resistors each of resistance R. then R_(12)
View SolutionThe resistance of each wire in the given figure is r. Find the equivalent resistance between the points A and B.
View Solutionसमान प्रतिरोध R के तार चित्रानुसार जुड़े हैं, तो x एवं y के मध्य तुल्य प्रतिरोध ज्ञात कीजिए।
View Solutionएक वर्ग एक तार का बना हुआ है, जिसकी प्रत्येक भुजा का प्रतिरोध R ओम है। विकर्ण के सिरों पर बिन्दुओं के मध्य प्रभावी प्रतिरोध होगा-
View SolutionIn the shown wire frame, each side of a square (the smallest square) has a resistance R. The equivalent resistance of the circuit between the points A and B is

View SolutionIn the shown wire frame, each side of a square (the smallest square) has a resistance R. The equivalent resistance of the circuit between the points A and B is
View SolutionIn a given network, each resistance has value of . The point X is connected to point A by a copper wire of negligible resistance and point Y is connected to point B by the same wire. The effective resistance between X and Y will be
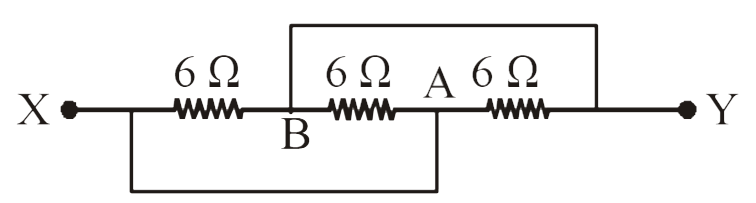
View SolutionIn a given network, each resistance has value of . The point X is connected to point A by a copper wire of negligible resistance and point Y is connected to point B by the same wire. The effective resistance between X and Y will be

View Solution