Find the electric field strength vector at the centre of a ball of radius R with volume charge density ρ = ar where a is a constant vector and r is a radius vector drawn from the balls centre.
Let us consider an elemental spherical shell of thickness dr. Thus surface charge density of the shell Thus using the above equation field strength due to this sperical shellHence the sought field strength
Related Solutions
Find the electric field strength vector at the centre of a ball of raiduius R with volume charge density rho implies ar , where a is a constant vector, and r is a radius vector drawn from the ball's centre.
View SolutionA ball of radius is uniformly charged with the volume density . Find the flux if the electric field strength vector across the balls section formed by the plane located at a distance from the centre of the ball.
View SolutionA shpere of radius r carries a surface charge a density sigma = ar , where a is a constant, vector and r is radius vector of a point of the sphere ralative to its centre. Find the electric field strength vector at the centre relative at the centrre of the sphere.
View SolutionFind the electric field strength vector if the potentail of this field has the form varphi = ar , where is a constatn vector, and r is the radius vector of point of the field.
View SolutionThe volume charge density in a spherical ball of radius R varies with distance r from the centre s where is a constant. The radius at which the field be maximum is
View SolutionA non-conducting spherical ball of radius R contains a spherically symmetric charge with volume charge density rho=kr^(2) where r is the distance form the centre of the ball and n is a constant what should be n such that the electric field inside the ball is directly proportional to square of distance from the centre?
View SolutionA system consits of a ball of radus carrying spherically symmetric charge and the surrounding space filled with a charge of volume density , wehre is a constant, is the distance from the centre of the ball. Find the ball's the charge at whcih the magnitude of the electric field strength vector is independent of outside the ball. How high is this strength ? The permittives of the ball and the surrounding space are assumed to be equal to unity.
View SolutionA system consists of a ball of radius R carrying a uniformly distributed charge q and the surrounding space filled with a charge of volume density rho = alpha//r , where alpha is a constant and r is the distance from the centre of the ball. Find the charge on the ball for which the magnitude of electric field strength outside the ball is constant? The dielectric constant of the ball and the surrounding may be taken equal to unity.
View SolutionA ball of radius R has a uniformly distributed charge Q. The surrounding space of the ball is filled with a volume charge density rho=(b)/(r) , where b is a constant and r is the distance from the centre of the ball. It was found that the magnitude of electric field outside the ball is independent of distance r. (a) Find the value of Q. (b) Find the magnitude of electric field outside the ball.
View SolutionThere is a hemisphere of radius R having a uniform volume charge density . Find the electric potential and field at the centre
View SolutionA non conducting sphere of radius a is charged uniform with volume charge density rho . There is a spherical cavity in the sphere with radius b. The position vector of centre of the cavity with respect to centre of the original sphere is vecC . Find the electric field at any point inside the cavity whose position vector is vecr with respect to centre of the original sphere.
View SolutionAn uncharged ball of radius R is placed at a point in space and the region outside (from R to measured from centre of the ball) the ball is non-uniformly charged with a charge density where 'C' is a positive constant and r is the distance of a point measured from centre of the ball.
Electric field intensity at a distance x from centre of the ball is
View SolutionThe volume charge density of a sphere carrying charge Q and of radius R is proportional to the square of the distance from the centre. The ratio of the magnitude of the electric field at a distance 2R from the centre to that at a distance of (R )/(2) from the centre is
View SolutionThe linear charge density on a ring of radius R is where is a constant and is angle of radius vector of any point on the ring with x-axis. The electric potential at centre of ring is
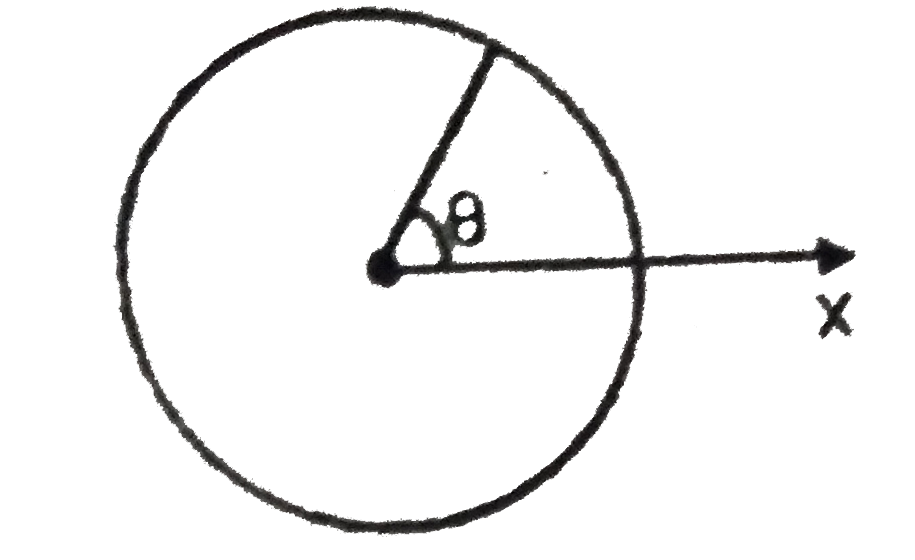
View SolutionThe linear charge density on a ring of radius R is lambda=lambda_0 sin (theta) where lambda_0 is a constant and theta is angle of radius vector of any point on the ring with x-axis. The electric potential at centre of ring is
View SolutionLet p=(Qr^(3))/(piR^(5)) be the volume charge density at distance r from the centre for a a soild sphere of radius R and charge Q. The electric field at r= (R)/(2) from the centre will be
View SolutionThe surface charge density of a thin charged disc of radius R is sigma . The value of the electric field at the centre of the disc is (sigma)/(2epsi_0) . With respect to the field at the centre, the electric field along the axis at a distance R from the centre of the disc
View SolutionA solid sphere of radius R has a spherical cavity of radius r as shown in the figure. If the volume charge density sigma is uniformly distributed over the whole volume of the sphere, then electric field strength at the centre of the sphere will be
View SolutionA solid sphere of radius R has a spherical cavity of radius r as shown in the figure. If the volume charge density sigma is uniformly distributed over the whole volume of the sphere, then electric field strength at the centre of the sphere will be
View SolutionThe volume charge density in a spherical ball of radius R varies with distence r from the centre as p(r)=p_(0)[1-((r)/(R))^(3)] , where, p_(0) is a constant. The radius at which the field would be maximum is
View Solution