A 50 g mass hangs at the end of a massless spring . When 20 g more are added to the end of the spring it stretches 7.0 cm more.a Find the spring constant.b If the 20 g are now removed what will be the period of the motion ?
According to question
Related Solutions
A mass hangs at the end of a massless spring. When more are added to the end of the spring, it stretches more. (a) Find the spring constant. (b) If the are now removed, what will be the period of the motion ?
View SolutionA 50 g mass hangs at the end of a massless spring. When 20 g more are added to the end of the spring, it stretches 7.0 cm more. (a) Find the spring constant. (b) If the 20 g are now removed, what will be the period of the motion ?
View SolutionA 0.2 kg of mass hangs at the end of a spring. When 0.02 kg more mass is added to the end of the spring, it stretches 7 cm more. If the 0.02 kg mass is removed, what will be the period of vibration of the system?
View SolutionA 0.2kg of mass hangs at the end of a spring. When 0.002kg more mass is added to the end of the spring, it stretches 7 cm more. If the 0.02 kg mass is removed what will be the period of vibration of the system?
View SolutionWhen a 20 g mass hangs attached to one end of a light spring of length 10 cm, the spring stretches by 2 cm. The mass is pulled down until the total length of the spring is 14 cm. The elastic energy, (in Joule) stored in the spring is :
View SolutionWhen a 20 g mass hangs attached to one end of a light spring of length 10 cm, the spring stretches by 2 cm. The mass is pulled down until the total length of the spring is 14 cm. The elastic energy, (in Joule) stored in the spring is :
View Solution400 ग्राम द्रव्यमान का पिण्ड , एक हलकी स्प्रिंग से लटका है 100 ग्राम द्रव्यमान का दूसरा पिण्ड इसमें रखने पर स्प्रिंग 5 सेमी और अधिक खिंच जाती है स्प्रिंग से लटके संयुक्त द्रव्यमानो का आवर्तकाल ज्ञात कीजिये (g =9.8 न्यूटन / किग्रा )
View SolutionWhen a mass of 100 g is suspended by a spring, it stretches by 2 cm. If 200 g is suspended by the spring and mass oscillates vertically. Calculate time period of oscillations.
View SolutionA spring is compressed by 10 cm by a ball of mass 20 g . What will be the potential energy of a spring if the force constant of the spring is 20 N cm^(-1) .
View SolutionA mass of 0.1 kg hangs at the end of a spring. When a mass of 0.01 kg more is added at the end of the spring, it stretches by 5 cm more. When the extra 0.01 kg mass is removed, determine the time period of vibration of the system.
View Solutionएक द्रव्यमानहीन स्प्रिंग की लम्बाई 10 सेमी है | स्प्रिंग से 500 ग्राम द्रव्यमान का पिण्ड लटकाने से इसकी लम्बाई में वृद्धि 5 सेमी होती है | गणना कीजिए : ( ii ) खिंची अवस्था में स्प्रिंग की लम्बाई l
View SolutionA body of mass 100 gm is suspended from a massless spring of natural length 1 m. If the spring stretches through a vertical distance of 20 cm, the potential energy stored in the spring is (g = )
View SolutionWhen a mass of 0.5 kg is suspended from the free end of a spring, it stretches the spring by 0.2m. This mass is removed and 0.25kg mass is attached to the same free end of the spring. If the mass is pulled down and released, what is its time period?( g=10ms^(-2) )
View SolutionWhen a mass of 0.5 kg is suspended from the free end of a spring, it stretches the spring by 0.2m. This mass is removed and 0.25kg mass is attached to the same free end of the spring. If the mass is pulled down and released, what is its time period? ()
View Solutionअज्ञात द्रव्यमान के पिण्ड को एक हल्के स्प्रिंग के निचले सिरे से लटकाने पर स्प्रिंग में ऊर्ध्वाधर खिचाव 9.8 सेमी है | स्प्रिंग के कम्पन का आवर्तकाल होगा :
View SolutionA spring of a negligible mass is stretched by a force of 20 g wt through a distance of 5 cms. A total mass of 50 g. is attached to the spring and set into oscillations. Find the periodic time of oscillation. Given
View SolutionWhen a 1.0kg mass hangs attached to a spring of length 50 cm, the spring stretches by 2 cm. The mass is pulled down until the length of the spring becomes 60 cm. What is the amount of elastic energy stored in the spring in this condition. if g = 10 m//s^(2).
View SolutionThree masses of 500 g , 300 g and 100 g are suspended at the end of a spring as shown and are in equilibrium. When the 500 g mass is removed suddenly, the system oscillates with a period of 2 s . When the 300 g mass is also removed, it will oscillate with period T . Find the value of T .
View SolutionThree masses of , and are suspended at the end of a spring as shown and are in equilibrium. When the mass is removed suddenly, the system oscillates with a period of . When the mass is also removed, it will oscillate with period . Find the value of .
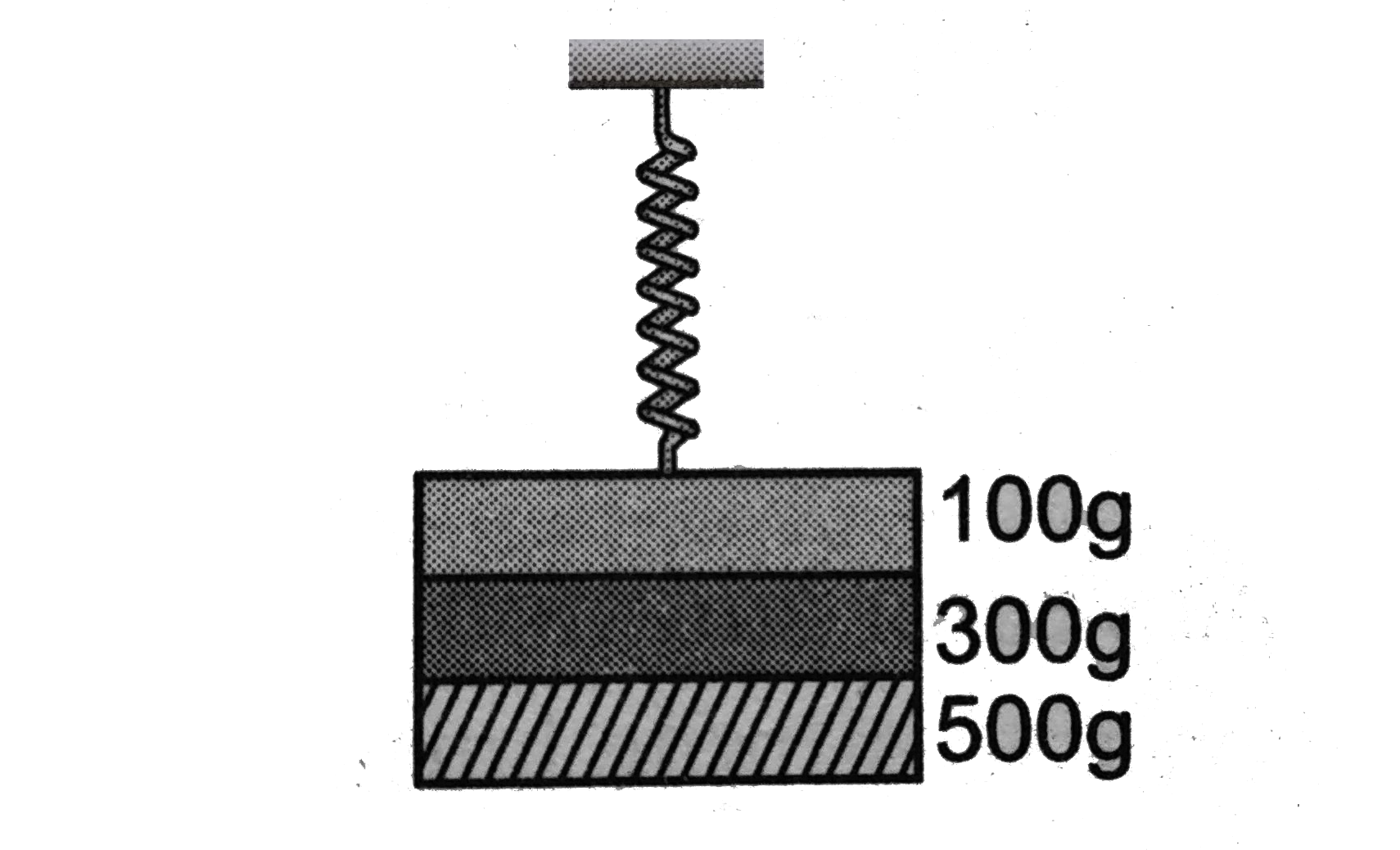
View SolutionWhen body of mass m is suspended from a spiral spring and spring gets stretched through a distance 20 cm if it is stretched below 20 cm and leave then what is period of oscillation?
View Solution