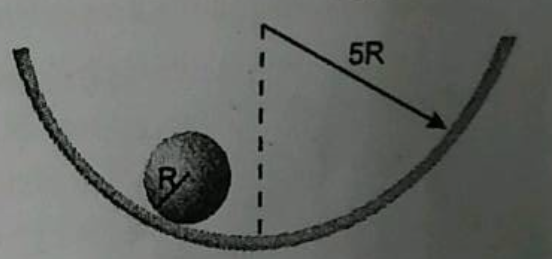
A solid sphere radius = R rolls without slipping in a cylindrical through radius = 5R . Find the time period of small oscillations.
For pure rolling to take place For small θ sin θ = θ being restoring in mature
Related Solutions
A solid sphere (radius = R) rolls without slipping in a cylindrical throuh (radius = 5R) . Findthe time period of small oscillations.
View SolutionA solid sphere (radius = R) rolls without slipping in a cylindrical throuh (radius = 5R) . Findthe time period of small oscillations.
View SolutionA solid sphere of (radius = R ) rolls without slipping in a cylindrical vessel (radius = 5R ). Find the time period of small of oscillations of the sphere in s^(-1) . Take R = (1)/(14)m and g = 10 m//s^(2) . (axis is cylinder is fixed and horizontal).
View SolutionA solid sphere of (radius ) rolls without slipping in a cylindrical vessel (radius ). Find the time period of small of oscillations of the sphere in . Take and . (axis is cylinder is fixed and horizontal).
View SolutionA ring of mass m and radius r rolls without slipping on a fixed hemispherical surface of radius R as shown. The time period of small oscillations of ring is 2pisqrt((n(R-r))/(3g)) then find the value of n.
View SolutionA ring of mass m and radius r rolls without slipping on a fixed hemispherical surface of radius R as shown. The time period of small oscillations of ring is 2pisqrt((n(R-r))/(3g)) then find the value of n.
View SolutionA spherical ball of mass m and radius r rolls without slipping on a rough concave surface of large radius . It makes small oscillations about the lowest point. Find the time period.
View SolutionA spherical ball of mass m and radius r rolls without slipping on a rough concave surface of large radius . It makes small oscillations about the lowest point. Find the time period.
View SolutionA spherical ball of mass m and radius r rolls without slipping on a rough concave surface of large radius R. It makes small oscillations about the lowest point. Find the time period.
View SolutionA spherical ball of mass m and radius r rolls without slipping on a rough concave surface of large radius R. It makes small oscillations about the lowest point. Find the time period.
View SolutionA spherical ball of mass m and radius r rolls without slipping on a rough concave surface of large radius R. It makes small oscillations about the lowest point. Find the time period.
View SolutionA semi cylindrical shell with negligible thickness oscillates without slipping on a horizontal surface. The time period of small oscillations is R
View SolutionThe ratio of the acceleration for a solid sphere (mass m and radius R) rolling down an incline of angle θ without slipping and slipping down the incline without rolling is,
View SolutionThe ratio of the accelerations for a solid sphere (mass .m. and radius .R.) rolling down and incline of angle or without slipping and slipping down the incline without rolling is
View SolutionThe ratio of the acceleration for a solid sphere (mass m and radius R) rolling down an incline of angle without slipping and slipping down the incline without rolling is,
View SolutionThe ratio of the accelerations for a solid sphere (mass 'm' and radius 'R') rolling down an incline of angle without slipping and slipping down the incline without rolling is
View SolutionThe ratio of the accelerations for a solid sphere (mass m and radius R) rolling down an incline of angle theta without slipping and slipping down the incline without rolling is
View SolutionThe ratio of the accelerations for a solid sphere (mass ) rolling down an incline of angle without slipping, and slipping down the incline without rolling is
View SolutionThe ratio of the acceleration for a solid sphere (mass m and radius R ) rolling down an incline of angle without slipping and slipping down the incline without rolling is
View SolutionThe ratio of the acceleration for a solid sphere (mass m and radius R) rolling down an incline of angle without slipping and slipping down the incline without rolling is,
View Solution