Demonstrate that the angular momentum M of the system of particles relative to a point O of the reference frame K can be represented asM = +[rcP] where is its proper angular momentum in the reference frame moving translationally and fixed to the centre of inertia rc is the radius vector of the centre of inertia relative to the point O p is the total momentum of the system of particles in the reference frame K.
On the basis of above equation we have concluded that; “in the C.M. frame the angular momentum of system of particles is independent of the choice of the point relative to which it is determined” and in accordance with the problem this is denoted by vector M.We denote the angular momentum of the system of particles relative to the point O by vector M. Since the internal and proper angular momentum in the C.M. frame does not depend on the choice of the point O this point may be taken coincident with the point O of the K-frame at a given moment of time. Then at that moment the radius vectors of all the particles in both reference frames are equal vector ri= vector ri and the velocities are related by the equation
Related Solutions
Demonstrate that the angular momentum M of the sytem of particles relative to a point O of the reference frame K can be represented as M=overset~M+[r_Cp] , where overset~M is its proper angular momentum (in the reference frame moving translationally and fixed to the centre of inertia), r_C is the radius vector of the centre of inertia relative to the point O, p is the total momentum of the system of particles in the reference frame K.
View SolutionThe reference frame, in which the centre of inertia of a given system of particles is at rest, translates with a velocity V relative to an inertial reference frame K. The mass of the system of particles equals m, and the total energy of the system in the frame of the centre of inertia is equal to . Find the total energy E of this system of particles in the reference frame K.
View SolutionLinear Momentum Of Two System Of Particle Relative To Centre Of Mass Frame
View SolutionA certain system of particles possesses a total momentum p and an angular momentum M relative to a point O. Find its angular momentum M^' relative to a point O^' whose position with respect to the point O is determined by the radius vector r_0 . Find out when the angular momentum of the system of particles does not depend on the choice of the point O.
View SolutionIf is the angular momentum about centre of mass of a system of particles, is the position vector of the center of mass relative to any point P and is the total momenta, then angular momentum of the system relative to point P is given by
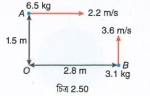
View Solutionদুটি বস্তুকণা A এবং B চিত্রে বর্ণিত তথ্য অনুযায়ী চলমান । O বিন্দুর সাপেক্ষে বস্তুকণাদ্বয়ের মোট কৌণিক ভরবেগ হবে
View SolutionA neutron with kinetic energy , where is its rest mass, strikes another, stationary, neutron. Determine:
(a) the combined kinetic energy of both neutrons in the frame of their centre of inertia and the momentum of each neutron in that frame,
(b) the velocity of the centre of inertia of this system of particles.
Instruction. Make use of the invariant remaining constant on transition from one inertial reference frame to another (E is the total energy of the system, p is its composite momentum).
View SolutionThree particles are moving as shown in the figure, Calculate the angular momentum of the third particle C , so that the angular momentum of system about point O becomes zero.
View SolutionThree particles are moving as shown in the figure, Calculate the angular momentum of the third particle C , so that the angular momentum of system about point O becomes zero.
View SolutionStatement-1: The kinetic energy of a system of particles is minimum from centre of mass frame of reference.
Statement-2 : The total momentum of a system as seen from centre of mass frame is minimum.
View SolutionTwo bodies of masses m_1 and m_2 are moving with velocity v_1 and v_2 respectively in the same direction. The total momentum of the system in the frame of reference attached to the centre of mass is ( v is relative velocity between the masses)
View SolutionA smooth horizontal disc rotates with a constant angular velocity about a stationary vertical axis passing through its centre, the point O. At a moment a disc is set in motion from that:
point with velocity . Find the angular momentum of the disc relative to the point O in the reference frame fixed to the disc. Make sure that this angular momentum is caused by the Coriolis force.
View Solutionएक द्रव्यमान M, X - अक्ष के समांतर नियत वेग से गतिमान है। मूलबिंदु के सापेक्ष इसका कोणीय संवेग घटेगा, बढ़ेगा या नियत रहेगा?
View SolutionIn centre-symmetrical system, the orbital angular momentum, a measure of the momentum of a particle travelling around the nucleus, is quantised. Its magnitude is
View SolutionIn centre-symmetrical system, the orbital angular momentum, a measure of the momentum of a particle travelling around the nucleus, is quantised. Its magnitude is
View SolutionDemonstrate that in the reference frame rotating with a constant angular velocity about a stationary axis a body of mass m experiences the resultant
(a) centrifugal force of inertia , where is the radius vector of the body's centre of inertia relative to the rotation axis,
(b) Coriolis force , where is the velocity of the body's centre of inertia in the rotating reference frame.
View SolutionWhy it is necessary for reference point in definition of angular momentum?
View Solutionएक कण मूल बिंदु से गुजरने वाली सीधी रेखा पर गतिशील है तो मूल बिंदु के सापेक्ष उसका कोणीय संवेग क्या होगा ?
View SolutionA ball of mass m moving with velocity v_0 experiences a head-on elastic collision with one of the spheres of a stationary rigid dumbbell as whown in figure. The mass of each sphere equals m//2 , and the distance between them is l . Disregarding the size of the spheres, find the proper angular momentum overset~M of the dumbbell after the collision, i.e. the angular momentum in the reference frame moving translationally and fixed to the dumbbell's centre of inertia.
View SolutionA closed system consists of two particles of masses m_1 and m_2 which move at right angles to each other with velocities v_1 and v_2 . Find: (a) the momentum of each particle and (b) the total kinetic energy of the two particles in the reference frame fixed to their centre of inertia.
View Solution