A smooth horizontal disc rotates with a constant angular velocity co about a stationary vertical axis passing through its centre the point O. At a moment t = O a disc is set in motion from that point with velocity vo. Find the angular momentum M t of the disc relative to the point O in the reference frame fixed to the disc. Make sure that this angular momentum is caused by the Coriolis force.
The Coriolis force is 2m vector v x vector ω. Here vector ω is along the z-axis vertical. The moving disc is moving with velocity v which is constant. The motion is along the x-axis say. Then the Coriolis force is along y-axis and has the magnitude 2mv0ω. At time t the distance of the centre of moving the disc from Thus the torque N due to the Coriolis force isThe constant is irrelevant and may be put equal to zero if the disc is originally set in motion from the point O. This discussion is approximate. The Coriolis force will cause the disc to swerve from straight line motion and thus cause deviation from the above formula which will be substantial for large t.
Related Solutions
A smooth horizontal disc rotates with a constant angular velocity about a stationary vertical axis passing through its centre, the point O. At a moment a disc is set in motion from that:
point with velocity . Find the angular momentum of the disc relative to the point O in the reference frame fixed to the disc. Make sure that this angular momentum is caused by the Coriolis force.
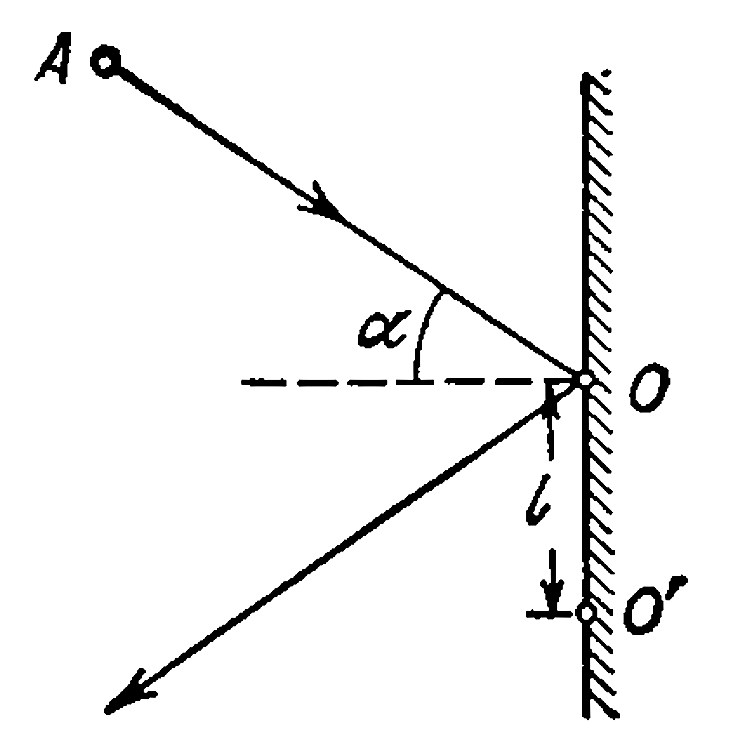
View SolutionA disc A of mass m sliding over a smooth horizontal surface with velocity experiences a perfectly elastic collision with a smooth stationary wall at a point O (figure). The angle between the motion direction of the disc and the normal of the wall is equal to . Find:
(a) the points relative to which the angular momentum M of the disc remains constant in this process,
(b) the magnitude of the increment of the vector of the disc's angular momentum relative to the point which is located in the plane of the disc's motion at the distance l from the point O.
View SolutionA horizontal disc rotates with a constant angular velocity omega=6.0rad//s about a vertical axis passing through its centre. A diameter of the disc with a velocity v^'=50cm//s which is constant relative to the disc. Find the force that the disc exerts on the body at the moment when it is located at the distance r=30cm from the rotation axis.
View SolutionA circular disc of radius R is rotating about its axis O with a uniform angular velocity omega"rad s"^(-1) as shown in the figure. The magnitude of the relative velocity of point A relative to point B on the disc is
View SolutionA circular disc of radius R is rotating about its axis O with a uniform angular velocity omega"rad s"^(-1) as shown in the figure. The magnitude of the relative velocity of point A relative to point B on the disc is
View SolutionA uniform disc of mass m and radius R rotates about a fixed vertical axis passing through its centre with angular velocity omega . A particle of same angular velocity mass m and moving horizontally with velocity 2omegaR towards centre of the disc collides and sticks to its rim. The impulse on the particle due to the disc is
View SolutionA uniform disc is rotating at a constant speed in a vertical plane about a fixed horizontal axis, passing through the centre of the disc. A piece of disc from its rim detaches itself from the disc at the instant when it is, on the same horizontal with the centre of the disc and moving upwards. lien about the fixed axis, the angular speed of the
View SolutionA circular disc is rotating in horizontal plane about vertical axis passing through its centre without friction with a person standing on the disc at its edge. If the person gently walks to centre of disc then its angular velocity
View SolutionA horizontal disc is rotating about a vertical axis passing through its centre. If an insect moves from centre to rim then the angular momentum of the system
View SolutionA horizontal disc is rotating about a vertical axis passing through its centre. If an insect moves from centre to rim then the angular momentum of the system
View SolutionA horizontal disc is rotating about a vertical axis passing through its centre. If an insect moves from centre to rim then the angular momentum of the system
View SolutionA disc of mass m and radius R is rolling on horizontal ground with linear velocity v. What is the angular momentum of the disc about an axis passing through bottommost point and perpendicular to the plane of motion ?
View SolutionA disc of mass m and radius R is rolling on horizontal ground with linear velocity v. What is the angular momentum of the disc about an axis passing through bottommost point and perpendicular to the plane of motion ?
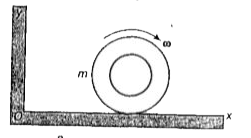
View SolutionA disc of mass M and radius R on a horizontal plane omega Rotating at an Angular Velocity [Chi 2.31] What is the value of the angular momentum of the disc relative to the origin O?
View SolutionA smooth horizontal disc rotates about the vertical axis (figure) with a constant angular velocity . A thin uniform rod of length performs small oscillation about the vertical axis fixed to the disc at a distance from the axis of the disc. Find the frequency of these oscillations.

View Solutionद्रव्यमान m तथा त्रिज्या R की एक डिस्क एक क्षैतिज तल पर कोणीय चाल से लुढ़क रही है जैसा कि चित्र में दर्शाया गया है। मूलबिन्दु O के परित: डिस्क का कोणीय संवेग है
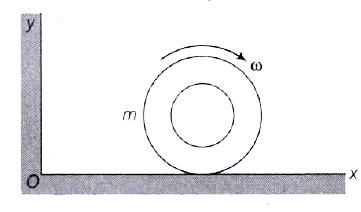
View SolutionA disc of mass M and radius R is rolling with angular speed omega on a horizontal plane as shown in figure. The magnitude of angular momentum of the disc about the origin O is
View SolutionA disc of mass M and radius R is rolling with angular speed won a horizontal plane as shown in figure. The magnitude of angular momentum of the disc about the origin O is
View Solutionद्रव्यमान m तथा त्रिज्या R की एक डिस्क एक क्षैतिज तल पर कोणीय चाल से लुढ़क रही है जैसा कि चित्र में दर्शाया गया है। मूलबिन्दु O के परित: डिस्क का कोणीय संवेग है
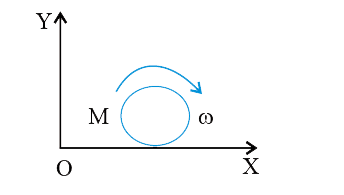
View SolutionA disc of mass M and radius R is rolling with angular speed w on horizontal plane as shown. The magnitude of angular momentum of the disc about the origin O is :
View Solution