One mole of an ideal gas with the adiabatic exponent γ goes through a polytropic process as a result of which the absolute temperature of the gas increases τ-fold. The polytropic constant equals n. Find the entropy increment of the gas in this process.
For the polytropic process with index npVn = constant Along this process
Related Solutions
One mole of an ideal gas with the adiabatic exponent goes through a polytropic process as a result of which the absolute temperature of the gas increases . The polytropic constant equal . Find the entropy increment of the gas in this process.
View SolutionAn ideal gas goes through a polytropic process. Find the polytropic exponent n if in this process the coefficient (a) of diffusion , (b) of viscosity , ( c) of heat conductivity remains constant.
View SolutionFind the molar heat capacity of an ideak gas in a polytropic process if the adiabatic exponent of the gas is equal to . At what values of the polytropic constant will the heat capacity of the gas be negative ?
View SolutionAn ideal gas goes through a cycle consisting of isothermal, polytropic, and adiabatic lines, with the isothermal process proceeding at the maximum temperature of the whole cycle. Find the efficiency of such a cycle if the absolute temperature varies within the cycle.
View SolutionIdeal gas and polytropic process
View SolutionOne mole of an ideal monoatomic gas is taken through a polytropic process = constant. The heat required to increase the temperature of the gas by is
View SolutionOne mole of an ideal monoatomic gas is taken through a polytropic process = constant. The heat required to increase the temperature of the gas by is
View SolutionThe heat capacity of an ideal gas in a polytropic process is C=Cv+0.1R.The value of polytropic exponent is :
View SolutionAn ideal gas with the adiabatic exponent y goes through a direct (clockwise) cycle, consisting of adiabatic, isobaric and isochoric lines. Find the efficiency of the cycle if in the adiabatic process the volume of the ideal gas increases n fold.
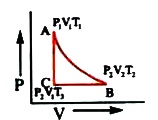
View SolutionFigure demonstrates a polytropic process (i.e. = constant ) for an ideal gas. The work done by the gas be in the process is
_S01_086_Q01.png)
View SolutionFigure demonstrates a polytropic process (i.e. = constant ) for an ideal gas. The work done by the gas be in the process is
_S01_086_Q01.png)
View SolutionFigure demonstrates a polytropic process (i.e. = constant ) for an ideal gas. The work done by the gas be in the process is
_S01_086_Q01.png)
View SolutionFind the entropy increment of v = 2.0 moles of an ideal gas whose adiabatic exponent gamma = 1.30 if, as a result of a certain process, the gas volume increased alpha = 2.0 times while the pressure dropped beta = 3.0 times.
View SolutionFor an ideal gas the ratio of specific heats is (C_(p))/(C_(v)) = gamma . The gas undergoes a polytropic process PV^(n) = a constant. Find the values of n for which the temperature of the gas increases when it rejects heat to the surrounding.
View Solution4 moles of an ideal monoatomic gas is heated isobarically so that its absolute temperature increases 2 times. Then the entropy increment of the gas in this process is
View Solution4 moles of an ideal monoatomic gas is heated isobarically so that its absolute temperature increases 2 times. Then the entropy increment of the gas in this process is
View SolutionIn the polytropic process = constant, is the gas cooled'or heated with increase in volume.
View SolutionAn ideal gas with the adiabatic exponent gamma goes through a cycle (Fig. 2.3) within which the absolute temperature varies tau-fold . Find the efficiency of this cycle. .
View SolutionOne mole of an ideal gas is carried through a thermodynamics cycle as shown in the figure. The cycle consists of an isochoric, an isothermal and an adiabatic process. Find the adiabatic exponent of the gas.
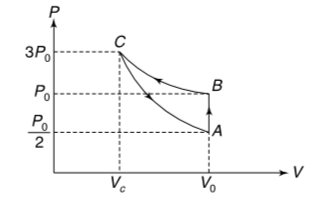
View SolutionThe volume of one mole of an ideal gas with adiabatic exponent gamma=1.4 is vaned according to law V=a//T where 'a' is a constant. Find amount of heat absorbed by gas in this process if gas temperature increases by 100 K.
View Solution